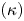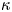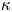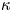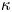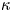1. Introduction
In a large variety of plasma applications, such as plasma processing and controlled fusion research, the dust particles mainly result from plasma–wall interactions and then enter the bulk plasma region across the sheath, which causes contamination in the plasma processing of integrated circuits and safety problems in fusion devices (Nitter Reference Nitter1996; Krasheninnikov, Smirnov & Rudakov Reference Krasheninnikov, Smirnov and Rudakov2011; Pustylnik et al. Reference Pustylnik, Pikalev, Zobnin, Semenov, Thomas and Petrov2021). On the other hand, fine dust probes can be used to study plasma-sheath characteristics since the dust particles immersed in the plasma become charged by the action of electron and ion fluxes (Samarian & James Reference Samarian and James2001; Beadles, Wang & Horanyi Reference Beadles, Wang and Horanyi2017). Due to the importance of the dusty plasma in the sheath, numerous modelling related studies have been carried out, including the dust particle charging process and dynamics in both radiofrequency (RF) and static sheaths (Nitter Reference Nitter1996; Hou, Wang & Miskovic Reference Hou, Wang and Miskovic2003; Bacharis, Coppins & Allen Reference Bacharis, Coppins and Allen2010; El Kaouini, Chatei & Bougdira Reference El Kaouini, Chatei and Bougdira2014; Khalilpour & Foroutan Reference Khalilpour and Foroutan2020; Zhao, Zhang & Wang Reference Zhao, Zhang and Wang2020).
For the dust particle charging process in an RF sheath, where quasi-neutrality breaks down and the large electric field gradients vary with time, Nitter introduced a model in which the electrons obey a Maxwellian distribution (Nitter Reference Nitter1996). Later, other authors studied the process in greater detail and addressed the issue of the determination of the dust particle charging process (Hou et al. Reference Hou, Wang and Miskovic2003; Bacharis et al. Reference Bacharis, Coppins and Allen2010; El Kaouini et al. Reference El Kaouini, Chatei and Bougdira2014; Missaoui, El Kaouini & Chatei Reference Missaoui, El Kaouini and Chatei2021). However, the electron distribution in plasma discharges is not perfectly Maxwellian if the system of particles is in non-thermal equilibrium. The RF sheath of plasma containing non-Maxwellian electrons has been investigated recently (Ou, An & Men Reference Ou, An and Men2019; Ou & Huang Reference Ou and Huang2020) and it is found that the supra-thermal electrons can modify the spatio-temporal variation of the plasma profile in the sheath region; such an effect of the non-Maxwellian electrons on the dust particle charge can be expected. According to the results of dust particles in a static sheath of non-Maxwellian plasma (Foroutan & Akhoundi Reference Foroutan and Akhoundi2012; Ou, Zhao & Lin Reference Ou, Zhao and Lin2018; El Ghani, Driouch & Chatei Reference El Ghani, Driouch and Chatei2019; Khalilpour & Foroutan Reference Khalilpour and Foroutan2020; Zhao et al. Reference Zhao, Zhang and Wang2020), it has been shown that the non-Maxwellian electrons can modify the profile of the dust particle when the dust components are relatively dense (Foroutan & Akhoundi Reference Foroutan and Akhoundi2012; El Ghani et al. Reference El Ghani, Driouch and Chatei2019; Khalilpour & Foroutan Reference Khalilpour and Foroutan2020), while they can change the dust particle charging process and levitation when the dust density is very low (Ou et al. Reference Ou, Zhao and Lin2018; Zhao et al. Reference Zhao, Zhang and Wang2020). Since the charge number of the dust particle in an RF sheath depends strongly on the RF field (Bacharis et al. Reference Bacharis, Coppins and Allen2010), the dust particle charging process in the non-Maxwellian electron RF sheath is more complex than in the static sheath. Here, we will discuss the effect of the supra-thermal electrons on the dust particle charging process by calculating the impact of both the instantaneous and time-averaged plasma parameters on the dust particles in the sheath.
Besides the electron distribution, we also relax some of restrictive assumptions involving the dust particle charging process in an RF sheath in this work in order to provide a wide extent of investigation. For example, it is assumed that the RF field frequency, ${\omega _{\textrm{RF}}}$![]() , is much larger than the ion plasma frequency ${\omega _{\textrm{pi}}}$
, is much larger than the ion plasma frequency ${\omega _{\textrm{pi}}}$![]() and smaller than the electron plasma frequency ${\omega _{\textrm{pe}}}$
and smaller than the electron plasma frequency ${\omega _{\textrm{pe}}}$![]() , i.e. ${\omega _{\textrm{pi}}} \ll {\omega _{\textrm{RF}}} \ll {\omega _{\textrm{pe}}}$
, i.e. ${\omega _{\textrm{pi}}} \ll {\omega _{\textrm{RF}}} \ll {\omega _{\textrm{pe}}}$![]() (Nitter Reference Nitter1996; Bacharis et al. Reference Bacharis, Coppins and Allen2010; Shotorban Reference Shotorban2012; El Kaouini et al. Reference El Kaouini, Chatei and Bougdira2014). Under this condition, the ions respond only to the time-averaged electric field and the electrons follow the instantaneous RF field. To show the dust particle charge in an RF sheath with s wide range of frequency, we discuss a dust particle immersed in the sheath of a plasma obtained from a self-consistent model for the structure of the RF driven by a sinusoidal current source at the wall in the ion cyclotron range of frequency (ICRF) (Edelberg & Aydil Reference Edelberg and Aydil1999; Hou et al. Reference Hou, Wang and Miskovic2003; Ou et al. Reference Ou, Zhao and Lin2018; Ou & Huang Reference Ou and Huang2020). Apart from the RF field frequency, the dust particle radius is usually assumed to be much smaller than the local electron Debye length. Based on the Whipple approximation (Whipple Reference Whipple1981) and the neglect of the plasma screening, the dust particle charge can be calculated from the Debye–Hückel potential. For some applications, such as in a fusion plasma, however, the dust particle size limit no longer holds because the dust particle size can be up to tens of microns (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011; Zhang et al. Reference Zhang, Ding, Peng, Yan, Chen, Zhu, Li and Si2021) while the local Debye length is relatively small due to the high plasma density. As a result, the Whipple approximation is only applicable in a limited range of dust size and the effect of the plasma screening on the dust particle charging must be taken into account. By using the model presented by Aussems et al. (Reference Aussems, Khrapak, Doğan, van de Sanden and Morgan2017), the modification of the effective screening length can be utilized to obtain the temporal evolution of the dust particle surface potential and the dust particle charge. In the present work, we take into account a dust particle radius comparable to or higher than the local Debye length under the tokamak plasma circumstance.
(Nitter Reference Nitter1996; Bacharis et al. Reference Bacharis, Coppins and Allen2010; Shotorban Reference Shotorban2012; El Kaouini et al. Reference El Kaouini, Chatei and Bougdira2014). Under this condition, the ions respond only to the time-averaged electric field and the electrons follow the instantaneous RF field. To show the dust particle charge in an RF sheath with s wide range of frequency, we discuss a dust particle immersed in the sheath of a plasma obtained from a self-consistent model for the structure of the RF driven by a sinusoidal current source at the wall in the ion cyclotron range of frequency (ICRF) (Edelberg & Aydil Reference Edelberg and Aydil1999; Hou et al. Reference Hou, Wang and Miskovic2003; Ou et al. Reference Ou, Zhao and Lin2018; Ou & Huang Reference Ou and Huang2020). Apart from the RF field frequency, the dust particle radius is usually assumed to be much smaller than the local electron Debye length. Based on the Whipple approximation (Whipple Reference Whipple1981) and the neglect of the plasma screening, the dust particle charge can be calculated from the Debye–Hückel potential. For some applications, such as in a fusion plasma, however, the dust particle size limit no longer holds because the dust particle size can be up to tens of microns (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011; Zhang et al. Reference Zhang, Ding, Peng, Yan, Chen, Zhu, Li and Si2021) while the local Debye length is relatively small due to the high plasma density. As a result, the Whipple approximation is only applicable in a limited range of dust size and the effect of the plasma screening on the dust particle charging must be taken into account. By using the model presented by Aussems et al. (Reference Aussems, Khrapak, Doğan, van de Sanden and Morgan2017), the modification of the effective screening length can be utilized to obtain the temporal evolution of the dust particle surface potential and the dust particle charge. In the present work, we take into account a dust particle radius comparable to or higher than the local Debye length under the tokamak plasma circumstance.
In the rest of this paper is organized as follows. Section 2 presents a one-dimensional model of the RF sheath containing supra-thermal electrons, which gives the profiles of the instantaneous and time-averaged plasma parameters, such as ion and electron densities and ion velocity. Section 3 concerns the effect of supra-thermal electrons on the dust particle charging process for different dust particle radii. Finally, the conclusions are drawn in § 4.
2. Sheath model
In the tokamak edge region, the plasma density ${n_s}$![]() is usually ${10^{17}}\unicode{x2013} {10^{18}}\;{\textrm{m}^{ - 3}}$
is usually ${10^{17}}\unicode{x2013} {10^{18}}\;{\textrm{m}^{ - 3}}$![]() , while the dust density is very low, e.g. only ${10^4}\;{\textrm{m}^{ - 3}}$
, while the dust density is very low, e.g. only ${10^4}\;{\textrm{m}^{ - 3}}$![]() in the DIII-D tokamak, and the charge number of a dust particle is ${10^4}\unicode{x2013} {10^5}$
in the DIII-D tokamak, and the charge number of a dust particle is ${10^4}\unicode{x2013} {10^5}$![]() (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011). Therefore, we can assume that a dust particle is isolated and the dust particles do not contribute to the total space charge. As shown in figure 1, the RF sheath is formed in front of the wall where the current disturbance source in ICRF is set and the collisions in the sheath are neglected. For the sheath of plasmas containing only deuterium ions and non-Maxwellian electrons, the profile of the sheath potential $\phi (x,t)$
(Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011). Therefore, we can assume that a dust particle is isolated and the dust particles do not contribute to the total space charge. As shown in figure 1, the RF sheath is formed in front of the wall where the current disturbance source in ICRF is set and the collisions in the sheath are neglected. For the sheath of plasmas containing only deuterium ions and non-Maxwellian electrons, the profile of the sheath potential $\phi (x,t)$![]() at any time t can be described by the Poisson equation
at any time t can be described by the Poisson equation
where $e,{\varepsilon _0}$![]() , ${n_i}(x,t)$
, ${n_i}(x,t)$![]() and ${n_e}(x,t)$
and ${n_e}(x,t)$![]() are the elementary charge, permittivity of free space and ion and electron densities, respectively. At the wall position $x = 0$
are the elementary charge, permittivity of free space and ion and electron densities, respectively. At the wall position $x = 0$![]() , the sheath potential $\phi (0,t) = {\phi _w}$
, the sheath potential $\phi (0,t) = {\phi _w}$![]() . At the plasma-sheath edge $x = {d_s}$
. At the plasma-sheath edge $x = {d_s}$![]() where ${d_s}$
where ${d_s}$![]() denotes the sheath thickness, the sheath potential is approximately zero, i.e. $\phi ({d_s},t) = 0$
denotes the sheath thickness, the sheath potential is approximately zero, i.e. $\phi ({d_s},t) = 0$![]() and the plasma satisfies the quasi-neutral condition ${n_{i,s}} = {n_{e,s}} = {n_s}$
and the plasma satisfies the quasi-neutral condition ${n_{i,s}} = {n_{e,s}} = {n_s}$![]() .
.

Figure 1. The geometry of the RF sheath model.
The usual Maxwellian distribution cannot describe the tokamak edge plasma under some conditions such as in the presence of the supra-thermal electrons coming from edge heating by the wave. The kappa distribution is a generalization of the Maxwellian distribution and can be formed due to wave–particle interactions (Abid, Ali & Muhammad Reference Abid, Ali and Muhammad2013). The power-law kappa $(\kappa )$![]() -distribution function can be expressed as
-distribution function can be expressed as

where $\varGamma$![]() is the standard gamma function and $\theta = \sqrt {(\kappa - 3/2)2{k_B}{T_e}/\kappa {m_e}}$
is the standard gamma function and $\theta = \sqrt {(\kappa - 3/2)2{k_B}{T_e}/\kappa {m_e}}$![]() , with Boltzmann's constant ${k_B}$
, with Boltzmann's constant ${k_B}$![]() , the electron temperature for a Maxwellian distribution ${T_e}$
, the electron temperature for a Maxwellian distribution ${T_e}$![]() and the electron mass ${m_e}$
and the electron mass ${m_e}$![]() . With the assumption of ${\omega _{\textrm{RF}}} \ll {\omega _{\textrm{pe}}}$
. With the assumption of ${\omega _{\textrm{RF}}} \ll {\omega _{\textrm{pe}}}$![]() , the electrons can instantaneously follow the RF field. By integrating over the $\kappa$
, the electrons can instantaneously follow the RF field. By integrating over the $\kappa$![]() -distribution velocity space, ${n_e}(x,t)$
-distribution velocity space, ${n_e}(x,t)$![]() is obtained (Hellberg et al. Reference Hellberg, Mace, Baluku, Kourakis and Saini2009)
is obtained (Hellberg et al. Reference Hellberg, Mace, Baluku, Kourakis and Saini2009)

With the fluid approximation, ${n_i}(x,t)$![]() and the ion velocity, ${v_i}(x,t)$
and the ion velocity, ${v_i}(x,t)$![]() , are determined by the ion continuity and momentum equations
, are determined by the ion continuity and momentum equations
here, ${m_i}$![]() is the ion mass and the pressure term ${p_i} = {n_i}{k_B}{T_i}$
is the ion mass and the pressure term ${p_i} = {n_i}{k_B}{T_i}$![]() is for the isothermal approximation with ion temperature ${T_i}$
is for the isothermal approximation with ion temperature ${T_i}$![]() . At the plasma-sheath edge, the ion velocity satisfies the Bohm criterion and ${v_{i,s}}\textrm{ = }\sqrt {({T_{\textrm{scr}}} + {T_i})/{m_i}}$
. At the plasma-sheath edge, the ion velocity satisfies the Bohm criterion and ${v_{i,s}}\textrm{ = }\sqrt {({T_{\textrm{scr}}} + {T_i})/{m_i}}$![]() for which the electron screening temperature ${T_{\textrm{scr}}} = (\kappa - 3/2){T_e}/(\kappa - 1/2)$
for which the electron screening temperature ${T_{\textrm{scr}}} = (\kappa - 3/2){T_e}/(\kappa - 1/2)$![]() can be obtained from ${T_{\textrm{scr}}} = e{n_e}(\phi )/(\textrm{d}{n_e}/\textrm{d}\phi ){|_{\phi = 0}}$
can be obtained from ${T_{\textrm{scr}}} = e{n_e}(\phi )/(\textrm{d}{n_e}/\textrm{d}\phi ){|_{\phi = 0}}$![]() .
.
By adopting the approach developed by Edelberg & Aydil (Reference Edelberg and Aydil1999), the RF sheath is model as a parallel combination of a diode, a capacitor and a current source, and then an equivalent circuit model is used to close the system of equations to determine the relationship between the instantaneous ${d_s}$![]() and ${\phi _w}$
and ${\phi _w}$![]() by the following current balance equation at the wall:
by the following current balance equation at the wall:
where ${A_0}$![]() is the wall area and the electron flux at the wall,
is the wall area and the electron flux at the wall,

The displacement current ${I_d}(t) = {C_{\textrm{cap}}}(\textrm{d}{\phi _w}/\textrm{d}t) + {\phi _w}(\textrm{d}{C_{\textrm{cap}}}/\textrm{d}t)$![]() with the time-dependent sheath capacitance ${C_{\textrm{cap}}} = {\varepsilon _0}{A_s}/{d_s}$
with the time-dependent sheath capacitance ${C_{\textrm{cap}}} = {\varepsilon _0}{A_s}/{d_s}$![]() . The applied current disturbance source at the wall is assumed to be sinusoidal with amplitude ${I_{\textrm{max}}}$
. The applied current disturbance source at the wall is assumed to be sinusoidal with amplitude ${I_{\textrm{max}}}$![]() .
.
The system (2.1)–(2.6) is normalized with the following dimensionless quantities: ${N_i} = {n_i}/{n_s}$![]() , ${N_e} = {n_e}/{n_s}$
, ${N_e} = {n_e}/{n_s}$![]() , $\varphi = e\phi /{k_B}{T_e}$
, $\varphi = e\phi /{k_B}{T_e}$![]() , ${u_i} = {v_i}/\sqrt {{k_B}{T_e}/{m_i}}$
, ${u_i} = {v_i}/\sqrt {{k_B}{T_e}/{m_i}}$![]() , $d = x/{\lambda _{D,i}}$
, $d = x/{\lambda _{D,i}}$![]() , ${\tau _i} = t/{t_0}$
, ${\tau _i} = t/{t_0}$![]() with ${t_0} = 2{\rm \pi} /{\omega _{\textrm{pi}}}$
with ${t_0} = 2{\rm \pi} /{\omega _{\textrm{pi}}}$![]() . Where ${\omega _{\textrm{pi}}} = \sqrt {{n_s}{e^2}/{m_i}{\varepsilon _0}}$
. Where ${\omega _{\textrm{pi}}} = \sqrt {{n_s}{e^2}/{m_i}{\varepsilon _0}}$![]() and ${\lambda _{D,i}} = \sqrt {{\varepsilon _0}{k_B}{T_i}/{n_s}{e^2}}$
and ${\lambda _{D,i}} = \sqrt {{\varepsilon _0}{k_B}{T_i}/{n_s}{e^2}}$![]() . With the sheath boundary conditions, we use the iteration method to solve numerically the set of closed nonlinear equations (2.1)–(2.6), and the iteration is repeated until the solutions converge to a self-consistent periodic steady state (Edelberg & Aydil Reference Edelberg and Aydil1999; Hou et al. Reference Hou, Wang and Miskovic2003; Ou et al. Reference Ou, An and Men2019; Ou & Huang Reference Ou and Huang2020). In this process, we can obtain the spatio-temporal distributions of the ion and electron densities, ion velocity and the sheath potential, and the corresponding time-averaged quantities, i.e. $\langle {n_i}(x)\rangle$
. With the sheath boundary conditions, we use the iteration method to solve numerically the set of closed nonlinear equations (2.1)–(2.6), and the iteration is repeated until the solutions converge to a self-consistent periodic steady state (Edelberg & Aydil Reference Edelberg and Aydil1999; Hou et al. Reference Hou, Wang and Miskovic2003; Ou et al. Reference Ou, An and Men2019; Ou & Huang Reference Ou and Huang2020). In this process, we can obtain the spatio-temporal distributions of the ion and electron densities, ion velocity and the sheath potential, and the corresponding time-averaged quantities, i.e. $\langle {n_i}(x)\rangle$![]() , $\langle {n_e}(x)\rangle$
, $\langle {n_e}(x)\rangle$![]() , $\langle {v_i}(x)\rangle$
, $\langle {v_i}(x)\rangle$![]() and $\langle \varphi (x)\rangle$
and $\langle \varphi (x)\rangle$![]() according to $\langle f(x)\rangle = \frac{1}{\tau }\int_0^\tau {f(x,t)\,\textrm{d}t}$
according to $\langle f(x)\rangle = \frac{1}{\tau }\int_0^\tau {f(x,t)\,\textrm{d}t}$![]() where $\tau = 2{\rm \pi} /{\omega _{\textrm{RF}}}$
where $\tau = 2{\rm \pi} /{\omega _{\textrm{RF}}}$![]() is the RF period. In our calculations, the RF sheath induced by the ICRF wave in a fusion plasma is considered with input parameters ${\omega _{\textrm{RF}}} = 50\;\textrm{MHz}$
is the RF period. In our calculations, the RF sheath induced by the ICRF wave in a fusion plasma is considered with input parameters ${\omega _{\textrm{RF}}} = 50\;\textrm{MHz}$![]() and ${I_{\textrm{max}}} = 2000\;\textrm{A}$
and ${I_{\textrm{max}}} = 2000\;\textrm{A}$![]() , and deuterium discharge is taken into account as an example, with ${T_i} = {T_e} = 10\;\textrm{eV}$
, and deuterium discharge is taken into account as an example, with ${T_i} = {T_e} = 10\;\textrm{eV}$![]() , ${n_s} = 3.0 \times {10^{17}}\;{\textrm{m}^{ - 3}}$
, ${n_s} = 3.0 \times {10^{17}}\;{\textrm{m}^{ - 3}}$![]() , ${A_0} = 0.\textrm{8}\;{\textrm{m}^2}$
, ${A_0} = 0.\textrm{8}\;{\textrm{m}^2}$![]() , as the typical parameters at an EAST-like tokamak during ICRF wave heating (Qin et al. Reference Qin, Zhang, Zhao, Wan, Franz, Wang, Yang, Yuan and Cheng2015). With above parameters, ${\lambda _{D,i}} \approx 4 \times {10^{ - 5}}\;\textrm{m}$
, as the typical parameters at an EAST-like tokamak during ICRF wave heating (Qin et al. Reference Qin, Zhang, Zhao, Wan, Franz, Wang, Yang, Yuan and Cheng2015). With above parameters, ${\lambda _{D,i}} \approx 4 \times {10^{ - 5}}\;\textrm{m}$![]() and ${\omega _{\textrm{pi}}} \approx 5 \times {10^{ - 8}}\;{\textrm{s}^{ - 1}}$
and ${\omega _{\textrm{pi}}} \approx 5 \times {10^{ - 8}}\;{\textrm{s}^{ - 1}}$![]() .
.
Figure 2 shows the variation of the sheath length, sheath potential drop, ratio density of electrons to ions and ion velocity near the wall with the time in two RF cycles for the different $\kappa$![]() values. As the $\kappa$
values. As the $\kappa$![]() value is decreased, both the sheath length and the sheath potential drop, and the ion velocity near the wall increases, while the ratio of the density of the electrons and ions decreases. This is due to the fact that the decrease of the $\kappa$
value is decreased, both the sheath length and the sheath potential drop, and the ion velocity near the wall increases, while the ratio of the density of the electrons and ions decreases. This is due to the fact that the decrease of the $\kappa$![]() value implies an increase of the high electron energy tail in the electron velocity distribution. The electrons with higher energy can easily overcome the decelerating electric force and penetrate the sheath, and then reduce the net positive space charge and, consequently, broaden the sheath. From the variation of the sheath potential drop with the $\kappa$
value implies an increase of the high electron energy tail in the electron velocity distribution. The electrons with higher energy can easily overcome the decelerating electric force and penetrate the sheath, and then reduce the net positive space charge and, consequently, broaden the sheath. From the variation of the sheath potential drop with the $\kappa$![]() value, it is indicated that the RF field becomes strong when the supra-thermal electron component is present. The profiles of time-averaged ion and electron densities, ion velocity and the sheath potential are shown in figure 3. It is evident that the sheath length increases with the decrease of the $\kappa$
value, it is indicated that the RF field becomes strong when the supra-thermal electron component is present. The profiles of time-averaged ion and electron densities, ion velocity and the sheath potential are shown in figure 3. It is evident that the sheath length increases with the decrease of the $\kappa$![]() value. For the same distance from the wall, the time-averaged ion and electron densities decrease while the ion velocity and sheath potential drop increase as the $\kappa$
value. For the same distance from the wall, the time-averaged ion and electron densities decrease while the ion velocity and sheath potential drop increase as the $\kappa$![]() value is decreased. From figures 2 and 3, we may expect that the dust particle charging process can be modified by the $\kappa$
value is decreased. From figures 2 and 3, we may expect that the dust particle charging process can be modified by the $\kappa$![]() value since the spatio-temporal variation of the sheath structure depends on the supra-thermal electrons.
value since the spatio-temporal variation of the sheath structure depends on the supra-thermal electrons.

Figure 2. The normalized sheath length (a), sheath potential (b), ratio density of electron to ion (c) and ion velocity (d) in two cycles for the different $\kappa$![]() values.
values.

Figure 3. The normalized time-averaged sheath quantities as the function of the distance from the wall: the ion density (a), ion velocity (b), the electron density (c) and sheath potential (d) for the different $\kappa$![]() values.
values.
3. Dust particle charging process
Dust particle charging is a dynamic process described by the charging equation
where ${Q_d}$![]() is the dust particle charge, ${I_{id}}$
is the dust particle charge, ${I_{id}}$![]() and ${I_{ed}}$
and ${I_{ed}}$![]() are the currents of the ions and electrons from the plasma to the dust particle, respectively. When discussing the dust particle charging process immersed in a collisionless plasma, the most common approach is through the orbital motion limited (OML) theory. For the dust particles in tokamak edge plasmas, the charging time of a dust particle is much shorter than the characteristic time of dust particle transport (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011), and then the dust particle velocity relative to the ion velocity can be neglected in the charging process. Based on OML theory, the ion current to a spherical dust particle (Whipple Reference Whipple1981; Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011)
are the currents of the ions and electrons from the plasma to the dust particle, respectively. When discussing the dust particle charging process immersed in a collisionless plasma, the most common approach is through the orbital motion limited (OML) theory. For the dust particles in tokamak edge plasmas, the charging time of a dust particle is much shorter than the characteristic time of dust particle transport (Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011), and then the dust particle velocity relative to the ion velocity can be neglected in the charging process. Based on OML theory, the ion current to a spherical dust particle (Whipple Reference Whipple1981; Krasheninnikov et al. Reference Krasheninnikov, Smirnov and Rudakov2011)

for a negative dust particle potential ${\varphi _d} < 0$![]() and
and

for s positive one.
The $\kappa$![]() -distribution electron current to the spherical dust particle (Abid et al. Reference Abid, Ali and Muhammad2013)
-distribution electron current to the spherical dust particle (Abid et al. Reference Abid, Ali and Muhammad2013)

for a negative dust particle potential ${\varphi _d} < 0$![]() and
and

for a positive one, where ${v_{ti}} = \sqrt {2{k_B}{T_i}/{m_i}}$![]() is the ion thermal speed and
is the ion thermal speed and
The relationship between ${Q_d}$![]() and ${\varphi _d}$
and ${\varphi _d}$![]() is given by ${Q_d} = {C_0}{\varphi _d}$
is given by ${Q_d} = {C_0}{\varphi _d}$![]() (Whipple Reference Whipple1981). Where ${C_0} = 4{\rm \pi} {\varepsilon _0}{r_d}(1 + {r_d}/{\lambda _D})$
(Whipple Reference Whipple1981). Where ${C_0} = 4{\rm \pi} {\varepsilon _0}{r_d}(1 + {r_d}/{\lambda _D})$![]() with ${\lambda _D} = {(\lambda _{D,i}^{ - 2} + \lambda _{D,e}^{ - 2})^{ - 1/2}}$
with ${\lambda _D} = {(\lambda _{D,i}^{ - 2} + \lambda _{D,e}^{ - 2})^{ - 1/2}}$![]() if ${r_d} < {\lambda _D}$
if ${r_d} < {\lambda _D}$![]() , and ${\lambda _D} = {(\lambda _{D,s}^{ - 2} + \lambda _{D,e}^{ - 2})^{ - 1/2}}$
, and ${\lambda _D} = {(\lambda _{D,s}^{ - 2} + \lambda _{D,e}^{ - 2})^{ - 1/2}}$![]() if ${r_d} > {\lambda _D}$
if ${r_d} > {\lambda _D}$![]() . The electron Debye length ${\lambda _{D,e}} = \sqrt {{\varepsilon _0}{k_B}[(\kappa - 3/2)/\kappa ]{T_e}/{n_s}e_0^2}$
. The electron Debye length ${\lambda _{D,e}} = \sqrt {{\varepsilon _0}{k_B}[(\kappa - 3/2)/\kappa ]{T_e}/{n_s}e_0^2}$![]() and the effective screening length ${\lambda _{D,s}} = \sqrt {1 + 0.48\sqrt {{\beta _s}} } {\lambda _{D,i}}$
and the effective screening length ${\lambda _{D,s}} = \sqrt {1 + 0.48\sqrt {{\beta _s}} } {\lambda _{D,i}}$![]() , with ${\beta _s} = (e{\varphi _d}/{k_B}{T_e})([(\kappa - 3/2)/\kappa ]{T_e}/{T_i})({r_d}/{\lambda _{D,i}})$
, with ${\beta _s} = (e{\varphi _d}/{k_B}{T_e})([(\kappa - 3/2)/\kappa ]{T_e}/{T_i})({r_d}/{\lambda _{D,i}})$![]() (Aussems et al. Reference Aussems, Khrapak, Doğan, van de Sanden and Morgan2017).
(Aussems et al. Reference Aussems, Khrapak, Doğan, van de Sanden and Morgan2017).
Linearizing (3.1) around an equilibrium charge ${Q_{d,\textrm{eq}}}$![]() ,we can obtain (Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996; Nitter Reference Nitter1996)
,we can obtain (Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996; Nitter Reference Nitter1996)

where ${Q_{d,1}}$![]() is a small perturbation from ${Q_{d,\textrm{eq}}}$
is a small perturbation from ${Q_{d,\textrm{eq}}}$![]() . Equation (3.7) has the solution ${Q_{d,1}} = {Q_{d,0}}\exp ( - {\omega _{\textrm{ch}}}t)$
. Equation (3.7) has the solution ${Q_{d,1}} = {Q_{d,0}}\exp ( - {\omega _{\textrm{ch}}}t)$![]() with the initial perturbed charge ${Q_{d,0}}$
with the initial perturbed charge ${Q_{d,0}}$![]() and the characteristic charging frequency ${\omega _{ch}} ={-} {(\partial ({I_{id}} + {I_{ed}})/\partial {Q_d})_{{Q_{d,\textrm{eq}}}}}$
and the characteristic charging frequency ${\omega _{ch}} ={-} {(\partial ({I_{id}} + {I_{ed}})/\partial {Q_d})_{{Q_{d,\textrm{eq}}}}}$![]() . The characteristic charging time ${\tau _{\textrm{ch}}} = 1/{\omega _{\textrm{ch}}}$
. The characteristic charging time ${\tau _{\textrm{ch}}} = 1/{\omega _{\textrm{ch}}}$![]() . Based on (3.2)–(3.5), we can obtain the rough dependence of ${\tau _{\textrm{ch}}}$
. Based on (3.2)–(3.5), we can obtain the rough dependence of ${\tau _{\textrm{ch}}}$![]() on the plasma parameters and dust particle radius
on the plasma parameters and dust particle radius
here, $\alpha \textrm{ = }{\kappa ^{3/2}}\varGamma (\kappa - 1/2)/\varGamma (\kappa + 1)$![]() is defined as a factor set to characterize the effect of the $\kappa$
is defined as a factor set to characterize the effect of the $\kappa$![]() value. The dependence of the $\alpha$
value. The dependence of the $\alpha$![]() value on the $\kappa$
value on the $\kappa$![]() value is shown in figure 4. From the small $\kappa$
value is shown in figure 4. From the small $\kappa$![]() value corresponding to the large $\alpha$
value corresponding to the large $\alpha$![]() value, it is indicated that the supra-thermal electrons can increase ${\tau _{\textrm{ch}}}$
value, it is indicated that the supra-thermal electrons can increase ${\tau _{\textrm{ch}}}$![]() . The $\alpha$
. The $\alpha$![]() value tends to 1 as the $\kappa$
value tends to 1 as the $\kappa$![]() value is increased, and the resultant ${\tau _{\textrm{ch}}}$
value is increased, and the resultant ${\tau _{\textrm{ch}}}$![]() or ${\omega _{\textrm{ch}}}$
or ${\omega _{\textrm{ch}}}$![]() tends to approach the Maxwellian electron case (Nitter Reference Nitter1996).
tends to approach the Maxwellian electron case (Nitter Reference Nitter1996).

Figure 4. The variation of the factor $\alpha$![]() with the $\kappa$
with the $\kappa$![]() value.
value.
Here, a dust particle with $1\;\mathrm{\mu }\textrm{m} < {r_d} < 50\;\mathrm{\mu }\textrm{m}$![]() is investigated based on ${\lambda _{D,i}} \approx 40\;\mathrm{\mu }\textrm{m}$
is investigated based on ${\lambda _{D,i}} \approx 40\;\mathrm{\mu }\textrm{m}$![]() calculated from the numerical parameters mentioned in the above section. For the sake of discussion, the following quantities are also defined. The charge number of a dust particle ${Z_d} = |{Q_d}/e|$
calculated from the numerical parameters mentioned in the above section. For the sake of discussion, the following quantities are also defined. The charge number of a dust particle ${Z_d} = |{Q_d}/e|$![]() . The time-averaged charge of a dust particle and charge number in an RF period are $\langle {Q_d}\rangle = \frac{1}{\tau }\int_0^\tau {{Q_d}(t)\,\textrm{d}t}$
. The time-averaged charge of a dust particle and charge number in an RF period are $\langle {Q_d}\rangle = \frac{1}{\tau }\int_0^\tau {{Q_d}(t)\,\textrm{d}t}$![]() and $\langle {\textrm{Z}_d}\rangle = \frac{1}{\tau }\int_0^\tau {{Z_d}(t)\,\textrm{d}t}$
and $\langle {\textrm{Z}_d}\rangle = \frac{1}{\tau }\int_0^\tau {{Z_d}(t)\,\textrm{d}t}$![]() , respectively. The root-mean-square of the charge number $Z_d^{\textrm{RMS}} = \sqrt {\frac{1}{\tau }\int_0^\tau {{{({Q_d}/e)}^2}\,\textrm{d}t} }$
, respectively. The root-mean-square of the charge number $Z_d^{\textrm{RMS}} = \sqrt {\frac{1}{\tau }\int_0^\tau {{{({Q_d}/e)}^2}\,\textrm{d}t} }$![]() . The root-mean-squared error $Z_d^{\textrm{RMSE}} = \sqrt {\frac{1}{\tau }\int_0^\tau {{{({Q_d}/e - \langle {Q_d}\rangle /e)}^2}\,\textrm{d}t} }$
. The root-mean-squared error $Z_d^{\textrm{RMSE}} = \sqrt {\frac{1}{\tau }\int_0^\tau {{{({Q_d}/e - \langle {Q_d}\rangle /e)}^2}\,\textrm{d}t} }$![]() , which is a quantity representing the scale of fluctuations of the dust particle charge, and the $\varDelta \textrm{Z}_d^{\textrm{amp}} = |Q_d^{\textrm{max}}/e - Q_d^{\textrm{min}}/e|/2$
, which is a quantity representing the scale of fluctuations of the dust particle charge, and the $\varDelta \textrm{Z}_d^{\textrm{amp}} = |Q_d^{\textrm{max}}/e - Q_d^{\textrm{min}}/e|/2$![]() which indicates the RF amplitude (Shotorban Reference Shotorban2012). The above corresponding quantities associated with ${\varphi _d}$
which indicates the RF amplitude (Shotorban Reference Shotorban2012). The above corresponding quantities associated with ${\varphi _d}$![]() also can be obtained based on ${Q_d} = {C_0}{\varphi _d}$
also can be obtained based on ${Q_d} = {C_0}{\varphi _d}$![]() .
.
Figure 5 shows the charging relaxation process of a dust particle for the different $\kappa$![]() values near sheath–wall interface and plasma-sheath edge. Near the sheath–wall interface, the charge number of the dust particle $({Z_d} = |{Q_d}/e|)$
values near sheath–wall interface and plasma-sheath edge. Near the sheath–wall interface, the charge number of the dust particle $({Z_d} = |{Q_d}/e|)$![]() increases rapidly with increasing time, and then reaches a quasi-stationary state with oscillation due to the strong RF field. The charging relaxation time of a dust particle with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$
increases rapidly with increasing time, and then reaches a quasi-stationary state with oscillation due to the strong RF field. The charging relaxation time of a dust particle with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$![]() is approximately $3 \times 2{\rm \pi} /{\omega _{\textrm{pi}}} = 2.04 \times {10^{ - 8}}\;\textrm{s}$
is approximately $3 \times 2{\rm \pi} /{\omega _{\textrm{pi}}} = 2.04 \times {10^{ - 8}}\;\textrm{s}$![]() while the charging relaxation time of dust particle with the same radius is of order microseconds in glow discharge plasma sheath (Nitter Reference Nitter1996). It is thus clear that dust particles in fusion circumstances are charged in a much shorter time than in a glow discharge plasma sheath. Figure 5 also shows that the charging relaxation time of a dust particle becomes shorter as the $\kappa$
while the charging relaxation time of dust particle with the same radius is of order microseconds in glow discharge plasma sheath (Nitter Reference Nitter1996). It is thus clear that dust particles in fusion circumstances are charged in a much shorter time than in a glow discharge plasma sheath. Figure 5 also shows that the charging relaxation time of a dust particle becomes shorter as the $\kappa$![]() value is increased. This is due to the fact that the increase of the $\kappa$
value is increased. This is due to the fact that the increase of the $\kappa$![]() value causes the decrease of the characteristic time of a dust particle, according to (3.8). Moreover, in the quasi-stationary state, the charge number of a dust particle increases significantly while the fluctuation of the dust particle charge changes a little. At the plasma-sheath edge, the RF oscillatory electric field caused by the applied current disturbance source becomes very small, and then the fluctuation of dust particle charge almost disappears. The charge number of the dust particle decreases as the $\kappa$
value causes the decrease of the characteristic time of a dust particle, according to (3.8). Moreover, in the quasi-stationary state, the charge number of a dust particle increases significantly while the fluctuation of the dust particle charge changes a little. At the plasma-sheath edge, the RF oscillatory electric field caused by the applied current disturbance source becomes very small, and then the fluctuation of dust particle charge almost disappears. The charge number of the dust particle decreases as the $\kappa$![]() value is decreased. This tendency is in agreement with the effect of the supra-thermal electrons on the charge number of the dust particle in a static sheath (Zhao et al. Reference Zhao, Zhang and Wang2020).
value is decreased. This tendency is in agreement with the effect of the supra-thermal electrons on the charge number of the dust particle in a static sheath (Zhao et al. Reference Zhao, Zhang and Wang2020).

Figure 5. The evolution of the dust particle charge as a function of time for the different $\kappa$![]() values with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$
values with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$![]() near the sheath–wall interface (a), and at the plasma-sheath edge (b).
near the sheath–wall interface (a), and at the plasma-sheath edge (b).
To further discuss the effect of the supra-thermal electrons on the dust particle charge, we tabulate the quantities such as $\langle {Z_d}\rangle ,Z_d^{\textrm{RMS}},\textrm{Z}_d^{\textrm{RMSE}}$![]() and $\varDelta \textrm{Z}_d^{\textrm{amp}}$
and $\varDelta \textrm{Z}_d^{\textrm{amp}}$![]() in table 1. For the variation of these quantities with the $\kappa$
in table 1. For the variation of these quantities with the $\kappa$![]() value, it is confirmed that the decrease in the supra-thermal electrons can cause a significant increase in the charge number of the dust particle, while causing a slight increase in the fluctuation of the dust particle charge for a dust particle with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$
value, it is confirmed that the decrease in the supra-thermal electrons can cause a significant increase in the charge number of the dust particle, while causing a slight increase in the fluctuation of the dust particle charge for a dust particle with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$![]() because ${\omega _{\textrm{ch}}} = 1/{\tau _{\textrm{ch}}} \propto {r_d}/\alpha$
because ${\omega _{\textrm{ch}}} = 1/{\tau _{\textrm{ch}}} \propto {r_d}/\alpha$![]() increases within a narrow range, as indicated in figure 4.
increases within a narrow range, as indicated in figure 4.
Table 1. Quasi-stationary state values in figure 5.

As shown in figure 5, the opposite effect of the $\kappa$![]() value on the dust particle charge near the sheath–wall interface and in the plasma-sheath edge can be found. To display the dependence of the dust particle charge modified by the $\kappa$
value on the dust particle charge near the sheath–wall interface and in the plasma-sheath edge can be found. To display the dependence of the dust particle charge modified by the $\kappa$![]() value on the position in the sheath, we plot the profiles of the time-averaged dust particle charge in the quasi-stationary state as a function of distance from the sheath–wall interface for the different $\kappa$
value on the position in the sheath, we plot the profiles of the time-averaged dust particle charge in the quasi-stationary state as a function of distance from the sheath–wall interface for the different $\kappa$![]() values in figure 6. It is found that the charge number of the dust particle increases from near the sheath–wall interface to the plasma-sheath edge. For the small $\kappa$
values in figure 6. It is found that the charge number of the dust particle increases from near the sheath–wall interface to the plasma-sheath edge. For the small $\kappa$![]() value, the increase of the charge number is faster than for the large $\kappa$
value, the increase of the charge number is faster than for the large $\kappa$![]() value. At the plasma-sheath edge, the charge number becomes larger than for the small $\kappa$
value. At the plasma-sheath edge, the charge number becomes larger than for the small $\kappa$![]() value. This is the result of the effect of the supra-thermal electrons on the sheath structure. Near the sheath–wall interface, a strong RF field is formed due to the applied current disturbance source at the wall and the ion current at the wall is balanced mainly by the sum of the displacement and the disturbance current (Ou et al. Reference Ou, An and Men2019). The smaller $\kappa$
value. This is the result of the effect of the supra-thermal electrons on the sheath structure. Near the sheath–wall interface, a strong RF field is formed due to the applied current disturbance source at the wall and the ion current at the wall is balanced mainly by the sum of the displacement and the disturbance current (Ou et al. Reference Ou, An and Men2019). The smaller $\kappa$![]() value causes a larger sheath potential drop, as indicated in figures 2 and 3, and then electron density becomes smaller while the ion flux does not change so much. As a result, the dust particle potential drop decreases as the $\kappa$
value causes a larger sheath potential drop, as indicated in figures 2 and 3, and then electron density becomes smaller while the ion flux does not change so much. As a result, the dust particle potential drop decreases as the $\kappa$![]() value is increased to keep the current from the plasma to the dust particle balance. At the plasma-sheath edge, the profiles of the plasma affected by the RF field is small, and the effect of the supra-thermal electrons on the dust particle charge is very similar to results obtained in a static sheath.
value is increased to keep the current from the plasma to the dust particle balance. At the plasma-sheath edge, the profiles of the plasma affected by the RF field is small, and the effect of the supra-thermal electrons on the dust particle charge is very similar to results obtained in a static sheath.

Figure 6. The profile of the time-averaged dust particle charge in the quasi-stationary state as a function of distance from the wall for the different $\kappa$![]() values with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$
values with ${r_d} = 10\;\mathrm{\mu }\textrm{m}$![]() . At the plasma-sheath edge positions ${d_s}/{\lambda _{D,i}}$
. At the plasma-sheath edge positions ${d_s}/{\lambda _{D,i}}$![]() : $8.6(\kappa = 3)$
: $8.6(\kappa = 3)$![]() , $7.3(\kappa = 5)$
, $7.3(\kappa = 5)$![]() , $6.6(\kappa = 10)$
, $6.6(\kappa = 10)$![]() .
.
According to (3.8), the characteristic charging time, or the characteristic charging frequency, depends on the dust particle radius and supra-thermal electrons. To reveal the interplay of the supra-thermal electrons and dust particle radius on the dust particle charging process, figure 7 shows the variation of the mean charge of the dust particle and fluctuation of the dust particle charge in a quasi-stationary state with the $\kappa$![]() value and ${r_d}$
value and ${r_d}$![]() . It is demonstrated that the mean charge of the dust particle depends strongly on both $\kappa$
. It is demonstrated that the mean charge of the dust particle depends strongly on both $\kappa$![]() and ${r_d}$
and ${r_d}$![]() , and a significant increase of $\langle {Z_d}\rangle$
, and a significant increase of $\langle {Z_d}\rangle$![]() can be found with the increase of both $\kappa$
can be found with the increase of both $\kappa$![]() and ${r_d}$
and ${r_d}$![]() . The fluctuation of the dust particle charge increases with ${r_d}$
. The fluctuation of the dust particle charge increases with ${r_d}$![]() , while it varies a little with the $\kappa$
, while it varies a little with the $\kappa$![]() value. It must be mentioned that the dust particle charge depends obviously on ${r_d}$
value. It must be mentioned that the dust particle charge depends obviously on ${r_d}$![]() since the dust particle charge is nearly proportional to the dust particle radius, but the dependence of the dust potential drop on ${r_d}$
since the dust particle charge is nearly proportional to the dust particle radius, but the dependence of the dust potential drop on ${r_d}$![]() may be very small in the quasi-stationary state according to (3.2)–(3.4). In figure 8, it is shown that the variations of the dust particle potential are almost the same for different radii of the dust particle, while the fluctuation of the dust particle potential increases with the dust particle radius under the same $\kappa$
may be very small in the quasi-stationary state according to (3.2)–(3.4). In figure 8, it is shown that the variations of the dust particle potential are almost the same for different radii of the dust particle, while the fluctuation of the dust particle potential increases with the dust particle radius under the same $\kappa$![]() value conditions. For comparison, the values of $\langle {\varphi _d}\rangle ,\varphi _d^{\textrm{RMS}},\varphi _d^{\textrm{RMSE}}$
value conditions. For comparison, the values of $\langle {\varphi _d}\rangle ,\varphi _d^{\textrm{RMS}},\varphi _d^{\textrm{RMSE}}$![]() and $\varDelta \varphi _d^{\textrm{amp}}$
and $\varDelta \varphi _d^{\textrm{amp}}$![]() are tabulated in table 2 in the quasi-stationary state for the cases associated with figure 8. It is found that the dust particle potential drop is almost independent of the dust particle radius, but fluctuation of the dust particle potential increases with the dust particle radius. Moreover, $\varphi _d^{\textrm{RMSE}}$
are tabulated in table 2 in the quasi-stationary state for the cases associated with figure 8. It is found that the dust particle potential drop is almost independent of the dust particle radius, but fluctuation of the dust particle potential increases with the dust particle radius. Moreover, $\varphi _d^{\textrm{RMSE}}$![]() and $\varDelta \varphi _d^{\textrm{amp}}$
and $\varDelta \varphi _d^{\textrm{amp}}$![]() are comparable for dust particles with small and large radii. Excepting $\varDelta \varphi _d^{\textrm{amp}}$
are comparable for dust particles with small and large radii. Excepting $\varDelta \varphi _d^{\textrm{amp}}$![]() for the large dust particle, our results are in good agreement with the results obtained in previous work (Shotorban Reference Shotorban2012) within an order of magnitude. The main reason causing the difference of $\varDelta \varphi _d^{\textrm{amp}}$
for the large dust particle, our results are in good agreement with the results obtained in previous work (Shotorban Reference Shotorban2012) within an order of magnitude. The main reason causing the difference of $\varDelta \varphi _d^{\textrm{amp}}$![]() for the large dust particle may be the ratio of ${\omega _{\textrm{ch}}}$
for the large dust particle may be the ratio of ${\omega _{\textrm{ch}}}$![]() and ${\omega _{\textrm{RF}}}$
and ${\omega _{\textrm{RF}}}$![]() (Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996). In our cases, because ${\omega _{\textrm{ch}}}$
(Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996). In our cases, because ${\omega _{\textrm{ch}}}$![]() is comparable to ${\omega _{\textrm{RF}}}$
is comparable to ${\omega _{\textrm{RF}}}$![]() , the dust particle charge only partially follows the RF field and has some time delay during an RF period, so $\varDelta \varphi _d^{\textrm{amp}}$
, the dust particle charge only partially follows the RF field and has some time delay during an RF period, so $\varDelta \varphi _d^{\textrm{amp}}$![]() increases but not much for the large dust particle. While for the case of ${\omega _{\textrm{ch}}} \gg {\omega _{\textrm{RF}}}$
increases but not much for the large dust particle. While for the case of ${\omega _{\textrm{ch}}} \gg {\omega _{\textrm{RF}}}$![]() presented by Shotorban (Reference Shotorban2012), the dust particle has enough time to change its charge during an RF period, and then $\varDelta \varphi _d^{\textrm{amp}}$
presented by Shotorban (Reference Shotorban2012), the dust particle has enough time to change its charge during an RF period, and then $\varDelta \varphi _d^{\textrm{amp}}$![]() increases an order of magnitude when the radius of the dust particle increases an order of magnitude. From the variation of $\varphi _d^{\textrm{RMSE}}$
increases an order of magnitude when the radius of the dust particle increases an order of magnitude. From the variation of $\varphi _d^{\textrm{RMSE}}$![]() and $\varDelta \varphi _d^{\textrm{amp}}$
and $\varDelta \varphi _d^{\textrm{amp}}$![]() with the $\kappa$
with the $\kappa$![]() value in table 2, it is also deduced that the fluctuation of the dust particle charge modified by the $\kappa$
value in table 2, it is also deduced that the fluctuation of the dust particle charge modified by the $\kappa$![]() value depends on the dust particle radius and the effect of the $\kappa$
value depends on the dust particle radius and the effect of the $\kappa$![]() value on the fluctuation of the dust particle charge becomes obvious for the large dust particle, since ${\omega _{\textrm{ch}}}$
value on the fluctuation of the dust particle charge becomes obvious for the large dust particle, since ${\omega _{\textrm{ch}}}$![]() or ${\tau _{\textrm{ch}}}$
or ${\tau _{\textrm{ch}}}$![]() for a change in ${Q_d}$
for a change in ${Q_d}$![]() is equal to the characteristic time for a change in ${\varphi _d}$
is equal to the characteristic time for a change in ${\varphi _d}$![]() (Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996).
(Melandsø et al. Reference Melandsø, Nitter, Aslaksen and Havnes1996).

Figure 7. The mean charge of the dust particle $\langle {Q_d}\rangle$![]() (a), and fluctuation of the dust particle charge $\varDelta \textrm{Z}_d^{\textrm{amp}}$
(a), and fluctuation of the dust particle charge $\varDelta \textrm{Z}_d^{\textrm{amp}}$![]() (b) near the sheath–wall interface in the quasi-stationary state as the functions of the $\kappa$
(b) near the sheath–wall interface in the quasi-stationary state as the functions of the $\kappa$![]() value and ${r_d}$
value and ${r_d}$![]() .
.

Figure 8. The evolution of the dust particle potential as a function of time for $\kappa = 3,\;{r_d} = 5\;\mathrm{\mu }\textrm{m}$![]() (a), $\kappa = 3,\;{r_d} = 50\;\mathrm{\mu }\textrm{m}$
(a), $\kappa = 3,\;{r_d} = 50\;\mathrm{\mu }\textrm{m}$![]() (b), $\kappa = 10,\;{r_d} = 5\;\mathrm{\mu }\textrm{m}$
(b), $\kappa = 10,\;{r_d} = 5\;\mathrm{\mu }\textrm{m}$![]() (c) and $\kappa = 10,\;{r_d} = 50\;\mathrm{\mu }\textrm{m}$
(c) and $\kappa = 10,\;{r_d} = 50\;\mathrm{\mu }\textrm{m}$![]() .
.
Table 2. Quasi-stationary state values in figure 8.

In the investigation of the dust particle charging process in an RF sheath, the time-averaged instead of instantaneous plasma parameters are used to calculate the dust particle charge under some conditions, if the exact shape of the dust particle potential variation during the RF period it not taken into account (Nitter Reference Nitter1996; Hou et al. Reference Hou, Wang and Miskovic2003; Bacharis et al. Reference Bacharis, Coppins and Allen2010; El Kaouini et al. Reference El Kaouini, Chatei and Bougdira2014). To compare the difference of the dust particle charge obtained from the instantaneous plasma parameters and that obtained from the time-averaged plasma parameters in the non-Maxwellian electron sheath, we plot the evolution of the dust particle charge with time near the sheath–wall interface for instantaneous and time-averaged plasma parameters in figure 9. The dashed line denotes ${\bar{Q}_d}$![]() obtained from the time-averaged plasma parameters in the sheath. The dust particle charge obtained from the instantaneous plasma parameters is seen to oscillate with the RF frequency and is followed by the dashed line closely for the different $\kappa$
obtained from the time-averaged plasma parameters in the sheath. The dust particle charge obtained from the instantaneous plasma parameters is seen to oscillate with the RF frequency and is followed by the dashed line closely for the different $\kappa$![]() values. However, the deviation degree of the dashed line in the quasi-stationary state increases with the decrease of the $\kappa$
values. However, the deviation degree of the dashed line in the quasi-stationary state increases with the decrease of the $\kappa$![]() value. It is indicated that for the case of the time scale of the dust particle motion in the sheath being much longer than the RF period, it is good approximation to calculate the dust particle charge by using the time-averaged plasma parameters in the sheath of a Maxwellian plasma, and the difference of dust particle charge obtained from between instantaneous and the time-averaged plasma parameters increases as the supra-thermal electron population is increased. Based on figure 9, we tabulate the values of ${\bar{Z}_d}({\bar{Z}_d} = |{\bar{Q}_d}/e|)$
value. It is indicated that for the case of the time scale of the dust particle motion in the sheath being much longer than the RF period, it is good approximation to calculate the dust particle charge by using the time-averaged plasma parameters in the sheath of a Maxwellian plasma, and the difference of dust particle charge obtained from between instantaneous and the time-averaged plasma parameters increases as the supra-thermal electron population is increased. Based on figure 9, we tabulate the values of ${\bar{Z}_d}({\bar{Z}_d} = |{\bar{Q}_d}/e|)$![]() , $\langle {Z_d}\rangle$
, $\langle {Z_d}\rangle$![]() and mean deviation $Z_d^{\textrm{MD}} = |(\langle {Z_d}\rangle - {\bar{Z}_d})/\langle {Z_d}\rangle |$
and mean deviation $Z_d^{\textrm{MD}} = |(\langle {Z_d}\rangle - {\bar{Z}_d})/\langle {Z_d}\rangle |$![]() in table 3 in the quasi-stationary state. We can see that the mean deviation of the charge number of a dust particle obtained from the time-averaged and instantaneous plasma parameters decreases as the $\kappa$
in table 3 in the quasi-stationary state. We can see that the mean deviation of the charge number of a dust particle obtained from the time-averaged and instantaneous plasma parameters decreases as the $\kappa$![]() value is increased, and the mean deviation always decreases for the larger dust particle under the same $\kappa$
value is increased, and the mean deviation always decreases for the larger dust particle under the same $\kappa$![]() value conditions.
value conditions.

Figure 9. The evolution of the dust particle charge as a function of time for different $\kappa$![]() values with ${r_d} = 5\;\mathrm{\mu }\textrm{m}$
values with ${r_d} = 5\;\mathrm{\mu }\textrm{m}$![]() (a) and ${r_d} = 10\;\mathrm{\mu }\textrm{m}$
(a) and ${r_d} = 10\;\mathrm{\mu }\textrm{m}$![]() (b). The dashed line denotes ${\bar{Q}_d}$
(b). The dashed line denotes ${\bar{Q}_d}$![]() obtained from the time-averaged plasma parameters in the sheath.
obtained from the time-averaged plasma parameters in the sheath.
Table 3. Quasi-stationary state values in figure 9.

4. Conclusion
In the framework of a one-dimensional dynamical model of a non-Maxwellian plasma RF sheath, the effect of the supra-thermal electrons on the dust particle charging process is studied theoretically by taking into account the collection of electrons and ions from the plasma. In the sheath model, the non-Maxwellian electrons are assumed to obey the kappa distribution in which the parameter $\kappa$![]() characterizes the deviation from a Maxwellian distribution, and the RF field is formed due to the applied current disturbance source at the wall in ICRF. By changing the $\kappa$
characterizes the deviation from a Maxwellian distribution, and the RF field is formed due to the applied current disturbance source at the wall in ICRF. By changing the $\kappa$![]() value, we have obtained self-consistently the influence of the supra-thermal electrons on both the instantaneous and time-averaged spatial distributions of some physical quantities in the sheath, such as the ion and electron densities and the ion velocity, which determine the dust particle charging process.
value, we have obtained self-consistently the influence of the supra-thermal electrons on both the instantaneous and time-averaged spatial distributions of some physical quantities in the sheath, such as the ion and electron densities and the ion velocity, which determine the dust particle charging process.
As the $\kappa$![]() value is decreased, our results show that the charge number of a dust particle decreases near the sheath–wall interface while it increases near the plasma-sheath edge. Due to the strong RF field near the sheath–wall interface, significant oscillation of the dust particle charge with time can be found. The fluctuation of the dust particle charge increases with the $\kappa$
value is decreased, our results show that the charge number of a dust particle decreases near the sheath–wall interface while it increases near the plasma-sheath edge. Due to the strong RF field near the sheath–wall interface, significant oscillation of the dust particle charge with time can be found. The fluctuation of the dust particle charge increases with the $\kappa$![]() value, and the increase caused by the $\kappa$
value, and the increase caused by the $\kappa$![]() value depends on the dust particle radius. For the small dust particle, the $\kappa$
value depends on the dust particle radius. For the small dust particle, the $\kappa$![]() value impacts weakly on the dust particle charge, and its impact increases with the dust particle radius. From the comparison of the dust particle charge obtained from instantaneous and time-averaged plasma parameters, it is demonstrated that the relaxation process of the dust particle calculated from time-averaged plasma parameters follows the tendency obtained from the instantaneous plasma parameters, but the corresponding dust particle charge in the quasi-stationary state deviates from the result obtained from the instantaneous plasma parameters as the $\kappa$
value impacts weakly on the dust particle charge, and its impact increases with the dust particle radius. From the comparison of the dust particle charge obtained from instantaneous and time-averaged plasma parameters, it is demonstrated that the relaxation process of the dust particle calculated from time-averaged plasma parameters follows the tendency obtained from the instantaneous plasma parameters, but the corresponding dust particle charge in the quasi-stationary state deviates from the result obtained from the instantaneous plasma parameters as the $\kappa$![]() value is decreased. For the various $\kappa$
value is decreased. For the various $\kappa$![]() values, the deviation always decreases when the dust particle radius becomes large.
values, the deviation always decreases when the dust particle radius becomes large.
Declaration of interests
The authors report no conflict of interest.
Funding
This work was supported by the National Key R&D Program of China under Grant No. 2017YFE0300404, and the National Natural Science Foundation of China with Grant No. 11775257.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.