Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T02:11:34.872Z Has data issue: false hasContentIssue false
  • English
  • Français

The development of magnetic field line wander in gyrokinetic plasma turbulence: dependence on amplitude of turbulence

Published online by Cambridge University Press:  02 May 2017

Sofiane Bourouaine  and
Gregory G. Howes Open the ORCID record for Gregory G. Howes [Opens in a new window]
Sofiane Bourouaine*
Affiliation:
Department of Physics and Astronomy, University of Iowa, Iowa City IA 54224, USA Physics and Space Sciences, Florida Institute of Technology, 150 w University blvd, Melbourne, FL 32904, USA
Gregory G. Howes
Affiliation:
Department of Physics and Astronomy, University of Iowa, Iowa City IA 54224, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a turbulent plasma not only manifests the transport of energy from large to small scales, but also can lead to a tangling of the magnetic field that threads through the plasma. The resulting magnetic field line wander can have a large impact on a number of other important processes, such as the propagation of energetic particles through the turbulent plasma. Here we explore the saturation of the turbulent cascade, the development of stochasticity due to turbulent tangling of the magnetic field lines and the separation of field lines through the turbulent dynamics using nonlinear gyrokinetic simulations of weakly collisional plasma turbulence, relevant to many turbulent space and astrophysical plasma environments. We determine the characteristic time 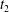$t_{2}$ for the saturation of the turbulent perpendicular magnetic energy spectrum. We find that the turbulent magnetic field becomes completely stochastic at time 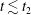$t\lesssim t_{2}$ for strong turbulence, and at 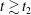$t\gtrsim t_{2}$ for weak turbulence. However, when the nonlinearity parameter of the turbulence, a dimensionless measure of the amplitude of the turbulence, reaches a threshold value (within the regime of weak turbulence) the magnetic field stochasticity does not fully develop, at least within the evolution time interval 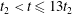$t_{2}<t\leqslant 13t_{2}$. Finally, we quantify the mean square displacement of magnetic field lines in the turbulent magnetic field with a functional form 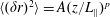$\langle (\unicode[STIX]{x1D6FF}r)^{2}\rangle =A(z/L_{\Vert })^{p}$ (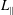$L_{\Vert }$ is the correlation length parallel to the magnetic background field 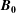$\boldsymbol{B}_{\mathbf{0}}$, $z$ is the distance along 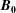$\boldsymbol{B}_{\mathbf{0}}$ direction), providing functional forms of the amplitude coefficient 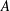$A$ and power-law exponent 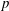$p$ as a function of the nonlinearity parameter.

Keywords

plasma nonlinear phenomenaplasma wavesspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 3 , June 2017 , 905830301
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abel, I. G., Barnes, M., Cowley, S. C., Dorland, W. & Schekochihin, A. A. 2008 Linearized model Fokker–Planck collision operators for gyrokinetic simulations. I. Theory. Phys. Plasmas 15 (12), 122509.Google Scholar
Alexandrova, O., Lacombe, C., Mangeney, A., Grappin, R. & Maksimovic, M. 2012 Solar wind turbulent spectrum at plasma kinetic scales. Astrophys. J. 760, 121.CrossRefGoogle Scholar
Barnes, M., Abel, I. G., Dorland, W., Ernst, D. R., Hammett, G. W., Ricci, P., Rogers, B. N., Schekochihin, A. A. & Tatsuno, T. 2009 Linearized model Fokker–Planck collision operators for gyrokinetic simulations. II. Numerical implementation and tests. Phys. Plasmas 16 (7), 072107.CrossRefGoogle Scholar
Beresnyak, A. 2013 Asymmetric diffusion of magnetic field lines. Astrophys. J. 767, L39 4 pp.Google Scholar
Bieber, J. W., Wanner, W. & Matthaeus, W. H. 1996 Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport. J. Geophys. Res. 101, 2511–2522.CrossRefGoogle Scholar
Biskamp, D., Schwarz, E. & Drake, J. F. 1996 Two-dimensional electron magnetohydrodynamic turbulence. Phys. Rev. Lett. 76, 1264–1267.Google Scholar
Biskamp, D., Schwarz, E., Zeiler, A., Celani, A. & Drake, J. F. 1999 Electron magnetohydrodynamic turbulence. Phys. Plasmas 6, 751–758.Google Scholar
Boldyrev, S. 2006 Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96 (11), 115002.CrossRefGoogle ScholarPubMed
Cho, J. & Lazarian, A. 2004 The anisotropy of electron magnetohydrodynamic turbulence. Astrophys. J. Lett. 615, L41–L44.Google Scholar
Cho, J. & Lazarian, A. 2009 Simulations of electron magnetohydrodynamic turbulence. Astrophys. J. 701, 236–252.CrossRefGoogle Scholar
Cho, J. & Vishniac, E. T. 2000 The anisotropy of magnetohydrodynamic Alfvénic turbulence. Astrophys. J. 539, 273–282.Google Scholar
Drake, D. J., Schroeder, J. W. R., Howes, G. G., Kletzing, C. A., Skiff, F., Carter, T. A. & Auerbach, D. W. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. IV. Laboratory experiment. Phys. Plasmas 20 (7), 072901.Google Scholar
Eyink, G. L. 2011 Stochastic flux freezing and magnetic dynamo. Phys. Rev. E 83 (5), 056405.Google Scholar
Eyink, G. L., Lazarian, A. & Vishniac, E. T. 2011 Fast magnetic reconnection and spontaneous stochasticity. Astrophys. J. 743, 51.Google Scholar
Frieman, E. A. & Chen, L. 1982 Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria. Phys. Fluids 25, 502–508.CrossRefGoogle Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447–488.Google Scholar
Ghosh, S. & Goldstein, M. L. 1997 Anisotropy in Hall MHD turbulence due to a mean magnetic field. J. Plasma Phys. 57, 129–154.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence II. Strong Alfvénic turbulence. Astrophys. J. 438, 763–775.Google Scholar
Guest, B. & Shalchi, A. 2012 Random walk of magnetic field lines in dynamical turbulence: a field line tracing method. II. Two-dimensional turbulence. Phys. Plasmas 19 (3), 032902.Google Scholar
Haas, F. A. & Thyagaraja, A. 1986 Conceptual and experimental bases of theories of anomalous transport in tokamaks. Phys. Rep. 143, 241–276.Google Scholar
Hatch, D. R., Pueschel, M. J., Jenko, F., Nevins, W. M., Terry, P. W. & Doerk, H. 2012 Origin of magnetic stochasticity and transport in plasma microturbulence. Phys. Rev. Lett. 108 (23), 235002.Google Scholar
Hatch, D. R., Pueschel, M. J., Jenko, F., Nevins, W. M., Terry, P. W. & Doerk, H. 2013 Magnetic stochasticity and transport due to nonlinearly excited subdominant microtearing modes. Phys. Plasmas 20 (1), 012307.Google Scholar
Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E. & Schekochihin, A. A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651, 590–614.CrossRefGoogle Scholar
Howes, G. G., Dorland, W., Cowley, S. C., Hammett, G. W., Quataert, E., Schekochihin, A. A. & Tatsuno, T. 2008b Kinetic simulations of magnetized turbulence in astrophysical plasmas. Phys. Rev. Lett. 100 (6), 065004–+.Google Scholar
Howes, G. G., Drake, D. J., Nielson, K. D., Carter, T. A., Kletzing, C. A. & Skiff, F. 2012 Toward astrophysical turbulence in the laboratory. Phys. Rev. Lett. 109 (25), 255001.Google Scholar
Howes, G. G. & Nielson, K. D. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. I. Asymptotic solution. Phys. Plasmas 20 (7), 072302.Google Scholar
Howes, G. G., Nielson, K. D., Drake, D. J., Schroeder, J. W. R., Skiff, F., Kletzing, C. A. & Carter, T. A. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. III. Theory for experimental design. Phys. Plasmas 20 (7), 072304.Google Scholar
Howes, G. G., TenBarge, J. M. & Dorland, W. 2011a A weakened cascade model for turbulence in astrophysical plasmas. Phys. Plasmas 18 (10), 102305.Google Scholar
Howes, G. G., TenBarge, J. M., Dorland, W., Quataert, E., Schekochihin, A. A., Numata, R. & Tatsuno, T. 2011b Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys. Rev. Lett. 107 (3), 035004.Google Scholar
Iroshnikov, P. S. 1963 Turbulence of a conducting fluid in a strong magnetic field. Astron. Zh. 40, 742–+.Google Scholar
Jokipii, J. R. 1966 Cosmic-ray propagation. I. Charged particles in a random magnetic field. Astrophys. J. 146, 480.Google Scholar
Jokipii, J. R. & Parker, E. N. 1968 Random walk of magnetic lines of force in astrophysics. Phys. Rev. Lett. 21, 44–47.CrossRefGoogle Scholar
Kraichnan, R. H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387.Google Scholar
Krommes, J. A., Oberman, C. & Kleva, R. G. 1983 Plasma transport in stochastic magnetic fields. Part 3. Kinetics of test particle diffusion. J. Plasma Phys. 30, 11–56.Google Scholar
Laval, G. 1993 Particle diffusion in stochastic magnetic fields. Phys. Fluids B 5, 711–721.Google Scholar
Lazarian, A. & Vishniac, E. T. 1999 Reconnection in a weakly stochastic field. Astrophys. J. 517, 700–718.Google Scholar
Lazarian, A., Vishniac, E. T. & Cho, J. 2004 Magnetic field structure and stochastic reconnection in a partially ionized gas. Astrophys. J. 603, 180–197.CrossRefGoogle Scholar
Lazarian, A. & Yan, H. 2014 Superdiffusion of cosmic rays: implications for cosmic ray acceleration. Astrophys. J. 784, 38.Google Scholar
Maron, J., Chandran, B. D. & Blackman, E. 2004 Divergence of neighboring magnetic-field lines and fast-particle diffusion in strong magnetohydrodynamic turbulence, with application to thermal conduction in galaxy clusters. Phys. Rev. Lett. 92 (4), 045001.Google Scholar
Maron, J. & Goldreich, P. 2001 Simulations of incompressible magnetohydrodynamic turbulence. Astrophys. J. 554, 1175–1196.Google Scholar
Matthaeus, W. H., Gray, P. C., Pontius, D. H. Jr & Bieber, J. W. 1995 Spatial structure and field-line diffusion in transverse magnetic turbulence. Phys. Rev. Lett. 75, 2136–2139.Google Scholar
Matthaeus, W. H., Oughton, S., Ghosh, S. & Hossain, M. 1998 Scaling of anisotropy in hydromagnetic turbulence. Phys. Rev. Lett. 81, 2056–2059.Google Scholar
Montgomery, D. & Matthaeus, W. H. 1995 Anisotropic modal energy transfer in interstellar turbulence. Astrophys. J. 447, 706.Google Scholar
Montgomery, D. & Turner, L. 1981 Anisotropic magnetohydrodynamic turbulence in a strong external magnetic field. Phys. Fluids 24, 825–831.CrossRefGoogle Scholar
Nevins, W. M., Wang, E. & Candy, J. 2011 Magnetic stochasticity in gyrokinetic simulations of plasma microturbulence. Phys. Rev. Lett. 106 (6), 065003.Google Scholar
Nielson, K. D., Howes, G. G. & Dorland, W. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution. Phys. Plasmas 20 (7), 072303.CrossRefGoogle Scholar
Numata, R., Howes, G. G., Tatsuno, T., Barnes, M. & Dorland, W. 2010 AstroGK: astrophysical gyrokinetics code. J. Comput. Phys. 229, 9347–9372.CrossRefGoogle Scholar
Oughton, S., Priest, E. R. & Matthaeus, W. H. 1994 The influence of a mean magnetic field on three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 280, 95–117.CrossRefGoogle Scholar
Pueschel, M. J., Hatch, D. R., Görler, T., Nevins, W. M., Jenko, F., Terry, P. W. & Told, D. 2013 Properties of high- $\unicode[STIX]{x1D6FD}$ microturbulence and the non-zonal transition. Phys. Plasmas 20 (10), 102301.CrossRefGoogle Scholar
Pueschel, M. J., Terry, P. W. & Hatch, D. R. 2014 Aspects of the non-zonal transitiona. Phys. Plasmas 21 (5), 055901.CrossRefGoogle Scholar
Qin, G. & Shalchi, A. 2013 The role of the Kubo number in two-component turbulence. Phys. Plasmas 20 (9), 092302.Google Scholar
Ragot, B. R. 2011 Statistics of field-line dispersal: random-walk characterization and supradiffusive regime. Astrophys. J. 728, 50.Google Scholar
Rechester, A. B. & Rosenbluth, M. N. 1978 Electron heat transport in a tokamak with destroyed magnetic surfaces. Phys. Rev. Lett. 40, 38–41.CrossRefGoogle Scholar
Ruffolo, D. & Matthaeus, W. H. 2013 Theory of magnetic field line random walk in noisy reduced magnetohydrodynamic turbulence. Phys. Plasmas 20 (1), 012308.Google Scholar
Sahraoui, F., Goldstein, M. L., Robert, P. & Khotyaintsev, Y. V. 2009 Evidence of a cascade and dissipation of solar-wind turbulence at the electron gyroscale. Phys. Rev. Lett. 102 (23), 231102–+.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. Ser. 182, 310–377.Google Scholar
Schlickeiser, R. 1989 Cosmic-ray transport and acceleration. I – Derivation of the kinetic equation and application to cosmic rays in static cold media. II – Cosmic rays in moving cold media with application to diffusive shock wave acceleration. Astrophys. J. 336, 243–293.Google Scholar
Shalchi, A. 2010a A unified particle diffusion theory for cross-field scattering: subdiffusion, recovery of diffusion, and diffusion in three-dimensional turbulence. Astrophys. J. 720, L127–L130.Google Scholar
Shalchi, A. 2010b Random walk of magnetic field lines in dynamical turbulence: a field line tracing method. I. Slab turbulence. Phys. Plasmas 17 (8), 082902.CrossRefGoogle Scholar
Shalchi, A. & Kolly, A. 2013 Analytical description of field-line random walk in Goldreich–Sridhar turbulence. Mon. Not. R. Astron. Soc. 431, 1923–1928.Google Scholar
Shalchi, A. & Kourakis, I. 2007a Analytical description of stochastic field-line wandering in magnetic turbulence. Phys. Plasmas 14 (9), 092903–092903.Google Scholar
Shalchi, A. & Kourakis, I. 2007b Random walk of magnetic field-lines for different values of the energy range spectral index. Phys. Plasmas 14 (11), 112901–112901.CrossRefGoogle Scholar
Shebalin, J. V., Matthaeus, W. H. & Montgomery, D. 1983 Anisotropy in mhd turbulence due to a mean magnetic field. J. Plasma Phys. 29, 525–547.Google Scholar
Snodin, A. P., Ruffolo, D., Oughton, S., Servidio, S. & Matthaeus, W. H. 2013 Magnetic field line random walk in models and simulations of reduced magnetohydrodynamic turbulence. Astrophys. J. 779, 56.Google Scholar
Spatschek, K. H. 2008 Aspects of stochastic transport in laboratory and astrophysical plasmas. Plasma Phys. Control. Fusion 50 (12), 124027.Google Scholar
Sridhar, S. & Goldreich, P. 1994 Toward a theory of interstellar turbulence. 1: weak Alfvenic turbulence. Astrophys. J. 432, 612–621.Google Scholar
TenBarge, J. M. & Howes, G. G. 2012 Evidence of critical balance in kinetic Alfvén wave turbulence simulations. Phys. Plasmas 19 (5), 055901.Google Scholar
TenBarge, J. M. & Howes, G. G. 2013 Current sheets and collisionless damping in kinetic plasma turbulence. Astrophys. J. 771, L27.Google Scholar
TenBarge, J. M., Howes, G. G. & Dorland, W. 2013 Collisionless damping at electron scales in solar wind turbulence. Astrophys. J. 774, 139.Google Scholar
TenBarge, J. M., Howes, G. G., Dorland, W. & Hammett, G. W. 2014 An oscillating Langevin antenna for driving plasma turbulence simulations. Comput. Phys. Commun. 185, 578–589.Google Scholar
Wang, E., Nevins, W. M., Candy, J., Hatch, D., Terry, P. & Guttenfelder, W. 2011 Electron heat transport from stochastic fields in gyrokinetic simulationsa. Phys. Plasmas 18 (5), 056111.CrossRefGoogle Scholar
Zimbardo, G., Pommois, P. & Veltri, P. 2006 Superdiffusive and subdiffusive transport of energetic particles in solar wind anisotropic magnetic turbulence. Astrophys. J. 639, L91–L94.Google Scholar
Zimbardo, G., Veltri, P., Basile, G. & Principato, S. 1995 Anomalous diffusion and Lévy random walk of magnetic field lines in three dimensional turbulence. Phys. Plasmas 2, 2653–2663.CrossRefGoogle Scholar
Zimbardo, G., Veltri, P. & Pommois, P. 2000 Anomalous, quasilinear, and percolative regimes for magnetic-field-line transport in axially symmetric turbulence. Phys. Rev. E 61, 1940–1948.Google Scholar
Zweben, S. J., Menyuk, C. R. & Taylor, R. J. 1979 Small-scale magnetic fluctuations inside the macrotor tokamak. Phys. Rev. Lett. 42, 1270–1274.Google Scholar