Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T16:33:40.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressibility in turbulent magnetohydrodynamics and passive scalar transport: mean-field theory

Part of: 50 years of Mean Field Electrodynamics

Published online by Cambridge University Press:  26 September 2018

I. Rogachevskii Open the ORCID record for I. Rogachevskii [Opens in a new window] ,
N. Kleeorin  and
A. Brandenburg Open the ORCID record for A. Brandenburg [Opens in a new window]
I. Rogachevskii*
Affiliation:
Department of Mechanical Engineering, Ben-Gurion University of the Negev, P.O. Box 653, 84105 Beer-Sheva, Israel Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
N. Kleeorin
Affiliation:
Department of Mechanical Engineering, Ben-Gurion University of the Negev, P.O. Box 653, 84105 Beer-Sheva, Israel Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
A. Brandenburg
Affiliation:
Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden Laboratory for Atmospheric and Space Physics, JILA and Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder, CO 80303, USA Department of Astronomy, AlbaNova University Center, Stockholm University, SE-10691 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a mean-field theory of compressibility effects in turbulent magnetohydrodynamics and passive scalar transport using the quasi-linear approximation and the spectral $\unicode[STIX]{x1D70F}$-approach. We find that compressibility decreases the $\unicode[STIX]{x1D6FC}$ effect and the turbulent magnetic diffusivity both at small and large magnetic Reynolds numbers, 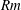$Rm$. Similarly, compressibility decreases the turbulent diffusivity for passive scalars both at small and large Péclet numbers, 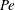$Pe$. On the other hand, compressibility does not affect the effective pumping velocity of the magnetic field for large 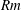$Rm$, but it decreases it for small 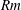$Rm$. Density stratification causes turbulent pumping of passive scalars, but it is found to become weaker with increasing compressibility. No such pumping effect exists for magnetic fields. However, compressibility results in a new passive scalar pumping effect from regions of low to high turbulent intensity both for small and large Péclet numbers. It can be interpreted as compressible turbophoresis of non-inertial particles and gaseous admixtures, while the classical turbophoresis effect exists only for inertial particles and causes them to be pumped to regions with lower turbulent intensity.

Keywords

astrophysical plasmasplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 5 , October 2018 , 735840502
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van Aartrijk, M. & Clercx, H. J. H. 2008 Preferential concentration of heavy particles in stably stratified turbulence. Phys. Rev. Lett. 100 (25), 254501.Google Scholar
Akhiezer, A. I. & Peletminskii, S. V. 1981 Methods of Statistical Physics. Pergamon.Google Scholar
Amir, G., Bar, N., Eidelman, A., Elperin, T., Kleeorin, N. & Rogachevskii, I. 2017 Turbulent thermal diffusion in strongly stratified turbulence: theory and experiments. Phys. Rev. Fluids 2 (6), 064605.Google Scholar
Armitage, P. J. 2010 Astrophysics of Planet Formation. Cambridge University Press.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Blackman, E. G. & Field, G. B. 2003 A new approach to turbulent transport of a mean scalar. Phys. Fluids 15 (11), L73–L76.Google Scholar
Brandenburg, A., Gressel, O., Käpylä, P. J., Kleeorin, N., Mantere, M. J. & Rogachevskii, I. 2012a New scaling for the alpha effect in slowly rotating turbulence. Astrophys. J. 762 (2), 127.Google Scholar
Brandenburg, A., Rädler, K.-H. & Kemel, K. 2012b Mean-field transport in stratified and/or rotating turbulence. Astron. Astrophys. 539, A35.Google Scholar
Brandenburg, A., Rädler, K.-H., Rheinhardt, M. & Käpylä, P. J. 2008 Magnetic diffusivity tensor and dynamo effects in rotating and shearing turbulence. Astrophys. J. 676 (1), 740.Google Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417 (1), 1–209.Google Scholar
Buchholz, J., Eidelman, A., Elperin, T., Grünefeld, G., Kleeorin, N., Krein, A. & Rogachevskii, I. 2004 Experimental study of turbulent thermal diffusion in oscillating grids turbulence. Exp. Fluids 36 (6), 879–887.Google Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32 (3), 565–568.Google Scholar
Chandrasekhar, S. 1943 Stochastic problems in physics and astronomy. Rev. Mod. Phys. 15 (1), 1.Google Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2013 Variable Density Fluid Turbulence, vol. 69. Springer Science & Business Media.Google Scholar
Crowe, C. T., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 2011 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
Csanady, G. T. 1980 Turbulent Diffusion in the Environment. Reidel.Google Scholar
Eidelman, A., Elperin, T., Kleeorin, N., Melnik, B. & Rogachevskii, I. 2010 Tangling clustering of inertial particles in stably stratified turbulence. Phys. Rev. E 81 (5), 056313.Google Scholar
Eidelman, A., Elperin, T., Kleeorin, N., Rogachevskii, I. & Sapir-Katiraie, I. 2006 Turbulent thermal diffusion in a multi-fan turbulence generator with imposed mean temperature gradient. Exp. Fluids 40 (5), 744–752.Google Scholar
Elperin, T., Kleeorin, N., Liberman, M. & Rogachevskii, I. 2013 Tangling clustering instability for small particles in temperature stratified turbulence. Phys. Fluids 25 (8), 085104.Google Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1995 Dynamics of the passive scalar in compressible turbulent flow: large-scale patterns and small-scale fluctuations. Phys. Rev. E 52 (3), 2617–2634.Google Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1996 Turbulent thermal diffusion of small inertial particles. Phys. Rev. Lett. 76 (2), 224–227.Google Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1997 Turbulent barodiffusion, turbulent thermal diffusion, and large-scale instability in gases. Phys. Rev. E 55 (3), 2713–2721.Google Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1998a Formation of inhomogeneities in two-phase low-mach-number compressible turbulent fluid flows. Intl J. Multiphase Flow 24 (7), 1163–1182.Google Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1998b Dynamics of particles advected by fast rotating turbulent fluid flow: fluctuations and large-scale structures. Phys. Rev. Lett. 81 (14), 2898–2901.Google Scholar
Elperin, T., Kleeorin, N., Rogachevskii, I. & Sokoloff, D. 2000 Passive scalar transport in a random flow with a finite renewal time: mean-field equations. Phys. Rev. E 61 (3), 2617–2625.Google Scholar
Elperin, T., Kleeorin, N., Rogachevskii, I. & Sokoloff, D. 2001 Mean-field theory for a passive scalar advected by a turbulent velocity field with a random renewal time. Phys. Rev. E 64 (2), 026304.Google Scholar
Elperin, T., Kleeorin, N., Rogachevskii, I. & Zilitinkevich, S. 2002 Formation of large-scale semiorganized structures in turbulent convection. Phys. Rev. E 66 (6), 066305.Google Scholar
Elperin, T., Kleeorin, N., Rogachevskii, I. & Zilitinkevich, S. S. 2006 Tangling turbulence and semi-organized structures in convective boundary layers. Boundary-layer Meteorol. 119 (3), 449–472.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Haugen, N. E. L., Kleeorin, N., Rogachevskii, I. & Brandenburg, A. 2012 Detection of turbulent thermal diffusion of particles in numerical simulations. Phys. Fluids 24 (7), 075106.Google Scholar
Hodgson, L. S. & Brandenburg, A. 1998 Turbulence effects in planetesimal formation. Astron. Astrophys. 330, 1169–1174.Google Scholar
Hubbard, A. 2015 Turbulent thermal diffusion: a way to concentrate dust in protoplanetary discs. Mon. Not. R. Astron. Soc. 456 (3), 3079–3089.Google Scholar
Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J. & Rogachevskii, I. 2012 Negative effective magnetic pressure in turbulent convection. Mon. Not. R. Astron. Soc. 422 (3), 2465–2473.Google Scholar
Kleeorin, N. & Rogachevskii, I. 2003 Effect of rotation on a developed turbulent stratified convection: the hydrodynamic helicity, the $\unicode[STIX]{x1D6FC}$ effect, and the effective drift velocity. Phys. Rev. E 67 (2), 026321.Google Scholar
Kleeorin, N. & Rogachevskii, I. 2018 Generation of large-scale vorticity in rotating stratified turbulence with inhomogeneous helicity: mean-field theory. J. Plasma Phys. 84 (3), 735840303.Google Scholar
Kleeorin, N., Rogachevskii, I. & Ruzmaikin, A. 1990 Magnetic force reversal and instability in a plasma with advanced magnetohydrodynamic turbulence. Sov. Phys. JETP 70, 878–883.Google Scholar
Krause, F. & Rädler, K.-H. 1980 Mean-Field Magnetohydrodynamics and Dynamo Theory. Pergamon.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Clarendon.Google Scholar
Mitra, D., Haugen, N. E. L. & Rogachevskii, I. 2018 Turbophoresis in forced inhomogeneous turbulence. Eur. Phys. J. Plus 133 (6), 35.Google Scholar
Moffatt, H. K. 1978 Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Monin, A. S. & Yaglom, A. M. 2013 Statistical Fluid Mechanics. Courier Corporation.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41 (2), 363–386.Google Scholar
Pandya, R. V. R. & Mashayek, F. 2002 Turbulent thermal diffusion and barodiffusion of passive scalar and dispersed phase of particles in turbulent flows. Phys. Rev. Lett. 88 (4), 044501.Google Scholar
Parker, E. N. 1979 Cosmical Magnetic Fields: Their Origin and Their Activity. Oxford University Press.Google Scholar
Piterbarg, L. & Ostrovskii, A. 2013 Advection and Diffusion in Random Media. Springer Science & Business Media.Google Scholar
Pouquet, A., Frisch, U. & Léorat, J. 1976 Strong MHD helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77 (2), 321–354.Google Scholar
Priest, E. R. 1982 Solar Magnetohydrodynamics. Reidel.Google Scholar
Rädler, K.-H., Brandenburg, A., Del Sordo, F. & Rheinhardt, M. 2011 Mean-field diffusivities in passive scalar and magnetic transport in irrotational flows. Phys. Rev. E 84 (4), 046321.Google Scholar
Rädler, K.-H., Kleeorin, N. & Rogachevskii, I. 2003 The mean electromotive force for MHD turbulence: the case of a weak mean magnetic field and slow rotation. Geophys. Astrophys. Fluid Dyn. 97 (3), 249–274.Google Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aero. Sci. 14 (6), 729–739.Google Scholar
Reeks, M. W. 1992 On the continuum equations for dispersed particles in nonuniform flows. Phys. Fluids 4 (6), 1290–1303.Google Scholar
Reeks, M. W. 2005 On model equations for particle dispersion in inhomogeneous turbulence. Intl J. Multiphase Flow 31 (1), 93–114.Google Scholar
Roberts, P. H. & Soward, A. M. 1975 A unified approach to mean field electrodynamics. Astron. Nachr. 296 (2), 49–64.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2000 Electromotive force for an anisotropic turbulence: intermediate nonlinearity. Phys. Rev. E 61 (5), 5202–5210.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2001 Nonlinear turbulent magnetic diffusion and mean-field dynamo. Phys. Rev. E 64 (5), 056307.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2003 Electromotive force and large-scale magnetic dynamo in a turbulent flow with a mean shear. Phys. Rev. E 68 (3), 036301.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2004 Nonlinear theory of a ‘shear–current’ effect and mean-field magnetic dynamos. Phys. Rev. E 70 (4), 046310.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2006 Small-scale magnetic buoyancy and magnetic pumping effects in a turbulent convection. Geophys. Astrophys. Fluid Dyn. 100 (3), 243–263.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2007 Magnetic fluctuations and formation of large-scale inhomogeneous magnetic structures in a turbulent convection. Phys. Rev. E 76 (5), 056307.Google Scholar
Rogachevskii, I. & Kleeorin, N. 2018 Mean-field theory of differential rotation in density stratified turbulent convection. J. Plasma Phys. 84 (2), 735840201.Google Scholar
Rogachevskii, I., Kleeorin, N., Brandenburg, A. & Eichler, D. 2012 Cosmic-ray current-driven turbulence and mean-field dynamo effect. Astrophys. J. 753 (1), 6.Google Scholar
Rogachevskii, I., Kleeorin, N., Käpylä, P. J. & Brandenburg, A. 2011 Pumping velocity in homogeneous helical turbulence with shear. Phys. Rev. E 84 (5), 056314.Google Scholar
Rogachevskii, I., Ruchayskiy, O., Boyarsky, A., Fröhlich, J., Kleeorin, N., Brandenburg, A. & Schober, J. 2017 Laminar and turbulent dynamos in chiral magnetohydrodynamics-i: theory. Astrophys. J. 846 (2), 153.Google Scholar
Rüdiger, G., Kitchatinov, L. L. & Hollerbach, R. 2013 Magnetic Processes in Astrophysics: Theory, Simulations, Experiments. Wiley-VCH.Google Scholar
Ruzmaikin, A., Shukurov, A. & Sokoloff, D. 1988 Magnetic Fields of Galaxies. Kluver.Google Scholar
Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M. & Christensen, U. R. 2005 Mean-field view on rotating magnetoconvection and a geodynamo model. Astron. Nachr. 326 (3–4), 245–249.Google Scholar
Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M. & Christensen, U. R. 2007 Mean-field concept and direct numerical simulations of rotating magnetoconvection and the geodynamo. Geophys. Astrophys. Fluid Dyn. 101 (2), 81–116.Google Scholar
Sofiev, M., Sofieva, V., Elperin, T., Kleeorin, N., Rogachevskii, I. & Zilitinkevich, S. S. 2009 Turbulent diffusion and turbulent thermal diffusion of aerosols in stratified atmospheric flows. J. Geophys. Res. 114, D18209.Google Scholar
Yokoi, N. & Brandenburg, A. 2016 Large-scale flow generation by inhomogeneous helicity. Phys. Rev. E 93 (3), 033125.Google Scholar
Yokoi, N. & Yoshizawa, A. 1993 Statistical analysis of the effects of helicity in inhomogeneous turbulence. Phys. Fluids 5 (2), 464–477.Google Scholar
Zaichik, L. I., Alipchenkov, V. M. & Sinaiski, E. G. 2008 Particles in Turbulent Flows. John Wiley & Sons.Google Scholar
Zeldovich, Ya. B., Ruzmaikin, A. A. & Sokoloff, D. D. 1990 The Almighty Chance. World Scientific.Google Scholar
Zeldovich, Ya. B., Ruzmaikin, A. A. & Sokolov, D. D. 1983 Magnetic Fields in Astrophysics. Gordon and Breach Science Publishers.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Lvov, V. & Rogachevskii, I. 2009 Energy-and flux-budget turbulence closure model for stably stratified flows. Part II. The role of internal gravity waves. Boundary-Layer Meteorol. 133 (2), 139–164.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I. & Esau, I. 2013 A hierarchy of energy-and flux-budget (EFB) turbulence closure models for stably-stratified geophysical flows. Boundary-Layer Meteorol. 146 (3), 341–373.Google Scholar