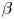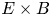1 Introduction
The high-confinement mode (H-mode) of plasma operation in a tokamak fusion experiment is characterised by the presence of a radially narrow region just inside the last closed flux surface (also called the separatrix) in which turbulent transport is strongly suppressed. In this edge transport barrier the profiles of electron and ion temperature as well as density are steep and their gradients large, forming a pedestal that lifts the rest of the profiles, ultimately improving fusion conditions in the core of the experiment or future reactor. For this reason, the H-mode is the baseline scenario of ITER, the world's largest fusion experiment, currently under construction in Cadarache, France.
In this study, we investigate small-scale turbulence in a pedestal of a standard Type-I ELMy H-mode from ASDEX Upgrade (AUG), which has been experimentally well diagnosed and analysed (Cavedon et al. Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017; Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020). Standard H-modes are unstable against edge-localised modes (ELMs), which expel large amounts of heat and particles (${\sim }10$![]() % of plasma energy; Cathey et al. Reference Cathey, Hoelzl, Lackner, Huijsmans, Dunne, Wolfrum, Pamela, Orain and Günter2020) tens of times per second, each time crashing the pedestal and causing unacceptably high heat loads on the divertor in future reactors. Therefore, special H-modes (EDA (Stimmel et al. Reference Stimmel, Gil, Görler, Cavedon, David, Dunne, Dux, Fischer, Jenko, Kallenbach, McDermott, Plank, Tardini and Told2022; Greenwald et al. Reference Greenwald1999; Gil et al. Reference Gil, Silva, Happel, Birkenmeier, Conway, Guimarais, Kallenbach, Pütterich, Santos, Schneider, Schubert, Seliunin, Silva, Stober, Stroth, Trier and Wolfrum2020), quiescent H-mode (Burrell et al. Reference Burrell2005) and small ELM/quasi-continuous exhaust (Harrer et al. Reference Harrer, Faitsch, Radovanovic, Wolfrum, Albert, Cathey, Cavedon, Dunne, Eich, Fischer, Griener, Hoelzl, Labit, Meyer and Aumayr2022)) and techniques (resonant magnetic perturbations (Wade et al. Reference Wade, Nazikian, de Grassie, Evans, Ferraro, Moyer, Orlov, Buttery, Fenstermacher, Garofalo, Lanctot, McKee, Osborne, Shafer, Solomon, Snyder, Suttrop, Wingen, Unterberg and Zeng2015; Suttrop et al. Reference Suttrop, Eich, Fuchs, Günter, Janzer, Herrmann, Kallenbach, Lang, Lunt, Maraschek, McDermott, Mlynek, Pütterich, Rott, Vierle, Wolfrum, Yu, Zammuto and Zohm2011, Reference Suttrop, Kirk, Bobkov, Cavedon, Dunne, McDermott, Meyer, Nazikian, Paz-Soldan, Ryan, Viezzer and Willensdorfer2018), vertical kicks (de la Luna et al. Reference de la Luna, Chapman, Rimini, Lomas, Saibene, Koechl, Sartori, Saarelma, Albanese, Flanagan, Maviglia, Parail, Sips and Solano2016) and pellets (Baylor et al. Reference Baylor, Lang, Allen, Combs, Commaux, Evans, Fenstermacher, Huijsmans, Jernigan, Lasnier, Leonard, Loarte, Maingi, Maruyama, Meitner, Moyer and Osborne2015)) for the suppression or mitigation of ELMs are an area of very active research. Nonetheless, well-developed standard H-mode pedestals remain useful as a prototype to study what turbulent transport mechanisms persist in this region of strong turbulence suppression.
% of plasma energy; Cathey et al. Reference Cathey, Hoelzl, Lackner, Huijsmans, Dunne, Wolfrum, Pamela, Orain and Günter2020) tens of times per second, each time crashing the pedestal and causing unacceptably high heat loads on the divertor in future reactors. Therefore, special H-modes (EDA (Stimmel et al. Reference Stimmel, Gil, Görler, Cavedon, David, Dunne, Dux, Fischer, Jenko, Kallenbach, McDermott, Plank, Tardini and Told2022; Greenwald et al. Reference Greenwald1999; Gil et al. Reference Gil, Silva, Happel, Birkenmeier, Conway, Guimarais, Kallenbach, Pütterich, Santos, Schneider, Schubert, Seliunin, Silva, Stober, Stroth, Trier and Wolfrum2020), quiescent H-mode (Burrell et al. Reference Burrell2005) and small ELM/quasi-continuous exhaust (Harrer et al. Reference Harrer, Faitsch, Radovanovic, Wolfrum, Albert, Cathey, Cavedon, Dunne, Eich, Fischer, Griener, Hoelzl, Labit, Meyer and Aumayr2022)) and techniques (resonant magnetic perturbations (Wade et al. Reference Wade, Nazikian, de Grassie, Evans, Ferraro, Moyer, Orlov, Buttery, Fenstermacher, Garofalo, Lanctot, McKee, Osborne, Shafer, Solomon, Snyder, Suttrop, Wingen, Unterberg and Zeng2015; Suttrop et al. Reference Suttrop, Eich, Fuchs, Günter, Janzer, Herrmann, Kallenbach, Lang, Lunt, Maraschek, McDermott, Mlynek, Pütterich, Rott, Vierle, Wolfrum, Yu, Zammuto and Zohm2011, Reference Suttrop, Kirk, Bobkov, Cavedon, Dunne, McDermott, Meyer, Nazikian, Paz-Soldan, Ryan, Viezzer and Willensdorfer2018), vertical kicks (de la Luna et al. Reference de la Luna, Chapman, Rimini, Lomas, Saibene, Koechl, Sartori, Saarelma, Albanese, Flanagan, Maviglia, Parail, Sips and Solano2016) and pellets (Baylor et al. Reference Baylor, Lang, Allen, Combs, Commaux, Evans, Fenstermacher, Huijsmans, Jernigan, Lasnier, Leonard, Loarte, Maingi, Maruyama, Meitner, Moyer and Osborne2015)) for the suppression or mitigation of ELMs are an area of very active research. Nonetheless, well-developed standard H-mode pedestals remain useful as a prototype to study what turbulent transport mechanisms persist in this region of strong turbulence suppression.
Turbulent transport in the pedestal is a key ingredient in multiple important aspects of edge physics. It influences the pedestal height and width as well as the dynamics of ELM cycles and its suppression is the basis for the formation of the edge transport barrier.
The simulation and quantitative prediction of turbulent pedestal transport, however, are challenging. The steep gradients in temperature and density, which characterise the pedestal centre, drive many of the classic core instabilities at once, causing the parallel presence and interaction of different instability types (e.g. ion temperature gradient (ITG) modes, electron temperature gradient (ETG) modes and trapped electron modes (TEMs)). Furthermore, the strong localisation of the drive poses fundamental challenges for heat flux calculations of ion-scale turbulence with usual local gyrokinetic simulations in which the driving gradients are assumed to be constant over the simulation domain. The strong drive causes large eddies, which require wide simulation domains to prevent the eddy from short-circuiting across the radial periodic boundary condition, which would yield unphysically large heat fluxes. Since the gradients are assumed to be constant in the local approach, the total drive of the system in a local simulation ends up much higher (strong drive in the whole simulation domain possibly hundreds of gyroradii wide) compared with the very localised steep gradient region ($\sim$![]() 10 gyroradii) and may prevent convergence at all.
10 gyroradii) and may prevent convergence at all.
Additionally, the steep gradients make the inclusion of electromagnetic fluctuations important, not only in order to include transport caused by electromagnetic instabilities (kinetic ballooning mode (KBM), micro-tearing mode (MTM)) but also because they can significantly influence the level of electrostatic heat flux.
In recent years the following picture of pedestal micro-instabilities and transport has emerged. Both MTM and ETG have been identified to be strong candidates for the most relevant instabilities in the steep gradient region of the pedestal (Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Valanju, Jenko, Told, Görler and Saarelma2016, Reference Hatch, Kotschenreuther, Mahajan, Merlo, Field, Giroud, Hillesheim, Maggi, Perez von Thun, Roach and Saarelma2019; Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim, Maggi, Giroud, Koechl, Parail, Saarelma, Solano and Chankin2019; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba, Ball and Ivanov2020; Chapman-Oplopoiou et al. Reference Chapman-Oplopoiou, Hatch, Field, Frassinetti, Hillesheim, Horvath, Maggi, Parisi, Roach, Saarelma and Walker2022; Halfmoon et al. Reference Halfmoon, Hatch, Kotschenreuther, Mahajan, Nelson, Kolemen, Curie, Diallo, Groebner, Hassan, Belli and Candy2022; Hassan et al. Reference Hassan, Hatch, Halfmoon, Curie, Kotchenreuther, Mahajan, Merlo, Groebner, Nelson and Diallo2022). In AUG, also TEMs and KBMs have been found to be relevant (Hatch et al. Reference Hatch, Told, Jenko, Doerk, Dunne, Wolfrum, Viezzer and Pueschel2015) and in JET-ILW (ITER-like Wall) ITG has been found to be present (Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017; Predebon et al. Reference Predebon, Hatch, Frassinetti, Horvath, Saarelma, Chapman-Oplopoiou, Görler and Maggi2023). In simulations with drift-kinetic electrons, KBMs and kinetic peeling-ballooning modes have been found to be important for pedestal stability (Wan et al. Reference Wan, Parker, Chen, Groebner, Yan, Pankin and Kruger2013). Most of these studies are based on local/linear, local/nonlinear, global/linear or reduced-$\beta$![]() simulations. However, to study which turbulent mechanisms drive transport under real pedestal conditions, global/nonlinear simulations at experimental $\beta$
simulations. However, to study which turbulent mechanisms drive transport under real pedestal conditions, global/nonlinear simulations at experimental $\beta$![]() values are indispensable. Such simulations are presented in this work.
values are indispensable. Such simulations are presented in this work.
In this paper, we present a radially resolved analysis of heat transport from pedestal top to foot covering ion and electron scales and including electrostatic as well as electromagnetic fluctuations. At the centre of our study are global, nonlinear, electromagnetic gyrokinetic simulations of an AUG pedestal, which have been enabled by an upgrade of the GENE code. They are supported by a detailed local, linear analysis of instabilities and dedicated local, nonlinear simulations of heat flux due to electron-scale fluctuations. We find that turbulent ion heat flux is present on the pedestal top and vanishes towards the steep gradient region. This is observed even without including the effect of $E\times B$![]() shear due to a radial electric field $E_r$
shear due to a radial electric field $E_r$![]() but is strongly enhanced by it. A combination of magnetic shear and pressure gradient is identified to locally stabilise modes and suppress heat flux. Our findings are in agreement with experimental observations that the ion heat flux reduces to neoclassic levels in the pedestal centre. Turbulent electron heat flux remains approximately constant across the pedestal but changes scale from dominantly ion-scale TEMs at the pedestal top to small-scale ETG-driven turbulence in the steep gradient region.
but is strongly enhanced by it. A combination of magnetic shear and pressure gradient is identified to locally stabilise modes and suppress heat flux. Our findings are in agreement with experimental observations that the ion heat flux reduces to neoclassic levels in the pedestal centre. Turbulent electron heat flux remains approximately constant across the pedestal but changes scale from dominantly ion-scale TEMs at the pedestal top to small-scale ETG-driven turbulence in the steep gradient region.
The paper is structured as follows: § 2 introduces the GENE code and its new upgrade for nonlinear, electromagnetic, global simulations, § 3 explains the experimental scenario investigated, § 4 shows the results of linear, local scans to characterise instabilities, § 5 shows the results of global and local nonlinear simulations and finally in § 6 conclusions are drawn.
2 Upgrade of the global electromagnetic GENE code
All simulations presented in this paper have been performed with the GENE code (genecode.org) (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011), which is a gyrokinetic, Eulerian, $\delta f$![]() Vlasov code that can perform a variety of simulation types, including: linear, nonlinear, electrostatic, electromagnetic, global, local and neoclassic. The presented simulations do not include the neoclassic drive term, as is the default for GENE simulations, to reduce computational costs. Therefore, the nonlinear simulations only include turbulent but not neoclassic transport.
Vlasov code that can perform a variety of simulation types, including: linear, nonlinear, electrostatic, electromagnetic, global, local and neoclassic. The presented simulations do not include the neoclassic drive term, as is the default for GENE simulations, to reduce computational costs. Therefore, the nonlinear simulations only include turbulent but not neoclassic transport.
It was found that a certain type, namely nonlinear, electromagnetic, global simulations, tended to be prone to numerical instabilities that could be avoided by artificially reducing plasma $\beta$![]() in simulations (e.g. Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Merlo, Field, Giroud, Hillesheim, Maggi, Perez von Thun, Roach and Saarelma2019). In effect, until now, nonlinear, global simulations could in most cases only be run with reduced $\beta$
in simulations (e.g. Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Merlo, Field, Giroud, Hillesheim, Maggi, Perez von Thun, Roach and Saarelma2019). In effect, until now, nonlinear, global simulations could in most cases only be run with reduced $\beta$![]() and not with experimental values. In this section the upgrade that overcomes this numerical instability is presented, following the proof-of-principle in Crandall (Reference Crandall2019) based on Reynders (Reference Reynders1993). The same electromagnetic model has recently also been implemented in GENE-3D (Wilms et al. Reference Wilms, Navarro, Merlo, Leppin, Görler, Dannert, Hindenlang and Jenko2021), the stellarator version of the GENE code. Related approaches are also being followed in gyrokinetic particle-in-cell codes (Mishchenko et al. Reference Mishchenko, Bottino, Hatzky, Sonnendrücker, Kleiber and Könies2017).
and not with experimental values. In this section the upgrade that overcomes this numerical instability is presented, following the proof-of-principle in Crandall (Reference Crandall2019) based on Reynders (Reference Reynders1993). The same electromagnetic model has recently also been implemented in GENE-3D (Wilms et al. Reference Wilms, Navarro, Merlo, Leppin, Görler, Dannert, Hindenlang and Jenko2021), the stellarator version of the GENE code. Related approaches are also being followed in gyrokinetic particle-in-cell codes (Mishchenko et al. Reference Mishchenko, Bottino, Hatzky, Sonnendrücker, Kleiber and Könies2017).
The GENE code solves the Vlasov–Maxwell system of equations to calculate the time evolution of a gyrocentre distribution $F$![]() in five-dimensional phase space. The Vlasov equation for one of the species reads
in five-dimensional phase space. The Vlasov equation for one of the species reads
where $\partial \boldsymbol {X}/\partial {t}$![]() contains the parallel and perpendicular (gradient-$B$
contains the parallel and perpendicular (gradient-$B$![]() , generalised $E\times B$
, generalised $E\times B$![]() , curvature) drifts $\partial \boldsymbol {X}/\partial {t}= v_{\parallel }\boldsymbol {\hat {b}}+B/B^*_{\parallel }(\boldsymbol {v}_{\boldsymbol {\nabla } B}+\boldsymbol {v}_{\chi }+\boldsymbol {v}_c)$
, curvature) drifts $\partial \boldsymbol {X}/\partial {t}= v_{\parallel }\boldsymbol {\hat {b}}+B/B^*_{\parallel }(\boldsymbol {v}_{\boldsymbol {\nabla } B}+\boldsymbol {v}_{\chi }+\boldsymbol {v}_c)$![]() , $\partial v _{\parallel }/\partial t$
, $\partial v _{\parallel }/\partial t$![]() is the parallel acceleration and $C$
is the parallel acceleration and $C$![]() symbolises a collision operator. The parallel acceleration depends on the time derivative of the fluctuating part of the magnetic vector potential $\bar {A}_{1\parallel }$
symbolises a collision operator. The parallel acceleration depends on the time derivative of the fluctuating part of the magnetic vector potential $\bar {A}_{1\parallel }$![]() (the overbar denotes a gyroaverage):
(the overbar denotes a gyroaverage):

where $c$![]() is the speed of light, $q$
is the speed of light, $q$![]() the charge and $m$
the charge and $m$![]() the mass of a given particle species. In the unmodified GENE code the time derivative of the fluctuating part $F_1$
the mass of a given particle species. In the unmodified GENE code the time derivative of the fluctuating part $F_1$![]() and $\bar {A}_{1\parallel }$
and $\bar {A}_{1\parallel }$![]() are combined and the distribution function which is evolved in time is $g_{1}=F_{1}-(q/m c) \bar {A}_{1\parallel } \partial F_0/ \partial v _{\parallel }$
are combined and the distribution function which is evolved in time is $g_{1}=F_{1}-(q/m c) \bar {A}_{1\parallel } \partial F_0/ \partial v _{\parallel }$![]() . This approach exhibits numerical instabilities in global, nonlinear, electromagnetic simulations. The numerical instabilities can be solved by retaining $F_1$
. This approach exhibits numerical instabilities in global, nonlinear, electromagnetic simulations. The numerical instabilities can be solved by retaining $F_1$![]() as the main distribution function and solving for $\bar {A}_{1\parallel }$
as the main distribution function and solving for $\bar {A}_{1\parallel }$![]() with an additional field equation derived from Ampère's law: $\nabla ^2_\perp A_{1\parallel } = (-4{\rm \pi} / c) j$
with an additional field equation derived from Ampère's law: $\nabla ^2_\perp A_{1\parallel } = (-4{\rm \pi} / c) j$![]() . By applying a time derivative to Ampère's law, using $E^{\text {ind}}_{\parallel }=(-1/ c)\partial A_{1\parallel }/\partial t$
. By applying a time derivative to Ampère's law, using $E^{\text {ind}}_{\parallel }=(-1/ c)\partial A_{1\parallel }/\partial t$![]() and writing the time derivative of $F_1$
and writing the time derivative of $F_1$![]() as $\partial F_1/\partial t=(q/m)\bar {E}^{\text {ind}}_{\parallel }\partial F_0/ \partial v _{\parallel } + R$
as $\partial F_1/\partial t=(q/m)\bar {E}^{\text {ind}}_{\parallel }\partial F_0/ \partial v _{\parallel } + R$![]() one finds
one finds

where the current $j$![]() has been expressed as a velocity space integral over the gyrocentre distribution function $F_1$
has been expressed as a velocity space integral over the gyrocentre distribution function $F_1$![]() , $R$
, $R$![]() denotes all remaining terms and the sum goes over all species $i$
denotes all remaining terms and the sum goes over all species $i$![]() . Collecting all terms containing $E^{\text {ind}}_{\parallel }$
. Collecting all terms containing $E^{\text {ind}}_{\parallel }$![]() on one side of the equation, the final field equation becomes
on one side of the equation, the final field equation becomes

which is solved numerically.
Effectively, $E^{\text {ind}}_{\parallel }=(-1/ c)\partial A_{1\parallel }/\partial t$![]() is treated as an additional independent field that is calculated from the distribution function $F_1$
is treated as an additional independent field that is calculated from the distribution function $F_1$![]() each time step. Next to the additional field equation for the plasma induction this approach requires an additional nonlinear term between the fields. In total these changes increase the computational time per time step by approximately 30 %. The new electromagnetic model is furthermore compatible with the use of block-structured velocity grids (Jarema et al. Reference Jarema, Bungartz, Görler, Jenko, Neckel and Told2017).
each time step. Next to the additional field equation for the plasma induction this approach requires an additional nonlinear term between the fields. In total these changes increase the computational time per time step by approximately 30 %. The new electromagnetic model is furthermore compatible with the use of block-structured velocity grids (Jarema et al. Reference Jarema, Bungartz, Görler, Jenko, Neckel and Told2017).
Before we discuss the results obtained with the presented upgrade in global, nonlinear simulations in § 5, the following two sections introduce the pedestal under consideration and its linear instabilities.
3 Experimental scenario: H-mode pedestal of AUG 31529
The particularly well-diagnosed and well-studied shot AUG 31529 (Cavedon et al. Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017; Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020) serves as the basis for our investigation. Shot AUG 31529 has neutral beam injection and electron cyclotron resonance heating, with a total heating power of $P_{\rm tot}=8.7$![]() MW, an on-axis $B$
MW, an on-axis $B$![]() -field of $-$
-field of $-$![]() 2.5 T and a plasma current of 0.8 MA. From this shot, we employ ELM-synchronised temperature and density profiles from Cavedon et al. (Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017) and pressure-constrained magnetic equilibria.
2.5 T and a plasma current of 0.8 MA. From this shot, we employ ELM-synchronised temperature and density profiles from Cavedon et al. (Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017) and pressure-constrained magnetic equilibria.
Figure 1 shows the profiles and corresponding gradient-scale lengths used in this study. Data points are from experimental measurements, lines are modified hyperbolic tangent (mtanh) fits. The $T_e$![]() and $n_e$
and $n_e$![]() data points show results of the integrated data analysis algorithm (Fischer et al. Reference Fischer, Fuchs, Kurzan, Suttrop and Wolfrum2010) combining measurements from lithium beam emission spectroscopy and electron cyclotron emission radiometry. The $T_i$
data points show results of the integrated data analysis algorithm (Fischer et al. Reference Fischer, Fuchs, Kurzan, Suttrop and Wolfrum2010) combining measurements from lithium beam emission spectroscopy and electron cyclotron emission radiometry. The $T_i$![]() data points show measurements of edge charge exchange recombination spectroscopy (CXRS) and averaged values of core CXRS. For more details, see Cavedon et al. (Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017). As input for the gyrokinetic simulations the pedestal profiles were fitted with mtanh functions as defined in Groebner et al. (Reference Groebner, Baker, Burrell, Carlstrom, Ferron, Gohil, Lao, Osborne, Thomas, West, Boedo, Moyer, McKee, Deranian, Doyle, Rettig, Rhodes and Rost2001) in the radial domain $\rho _{\rm tor}=[0.8,1]$
data points show measurements of edge charge exchange recombination spectroscopy (CXRS) and averaged values of core CXRS. For more details, see Cavedon et al. (Reference Cavedon, Pütterich, Viezzer, Laggner, Burckhart, Dunne, Fischer, Lebschy, Mink, Stroth, Willensdorfer and Wolfrum2017). As input for the gyrokinetic simulations the pedestal profiles were fitted with mtanh functions as defined in Groebner et al. (Reference Groebner, Baker, Burrell, Carlstrom, Ferron, Gohil, Lao, Osborne, Thomas, West, Boedo, Moyer, McKee, Deranian, Doyle, Rettig, Rhodes and Rost2001) in the radial domain $\rho _{\rm tor}=[0.8,1]$![]() : $\text {mtanh}(z) = a((1+\alpha z)e^z-e^{-z})/(e^z+e^{-z})+b$
: $\text {mtanh}(z) = a((1+\alpha z)e^z-e^{-z})/(e^z+e^{-z})+b$![]() , where $z=(r_{\rm sym}-r)/h_{\rm wid}$
, where $z=(r_{\rm sym}-r)/h_{\rm wid}$![]() . The uncertainty of the fits has been estimated by varying the fit parameters within a $3\sigma$
. The uncertainty of the fits has been estimated by varying the fit parameters within a $3\sigma$![]() interval of the best fit, where the standard deviation $\sigma$
interval of the best fit, where the standard deviation $\sigma$![]() was determined from the least-squares fit. Fit parameters were varied such that profiles with maximal and minimal average gradient were achieved. For the high-gradient case we choose the parameters $[a+3\sigma _a, b+3\sigma _b, r_{\rm sym}-3\sigma _r, h_{\rm wid}-3\sigma _h, \alpha +3\sigma _\alpha ]$
was determined from the least-squares fit. Fit parameters were varied such that profiles with maximal and minimal average gradient were achieved. For the high-gradient case we choose the parameters $[a+3\sigma _a, b+3\sigma _b, r_{\rm sym}-3\sigma _r, h_{\rm wid}-3\sigma _h, \alpha +3\sigma _\alpha ]$![]() and for the low-gradient case $[a-3\sigma _a, b-3\sigma _b, r_{\rm sym}+3\sigma _r, h_{\rm wid}+3\sigma _h, \alpha -3\sigma _\alpha ]$
and for the low-gradient case $[a-3\sigma _a, b-3\sigma _b, r_{\rm sym}+3\sigma _r, h_{\rm wid}+3\sigma _h, \alpha -3\sigma _\alpha ]$![]() . The range of gradients spanned by these fits is shown by the shaded areas in the gradient-scale lengths plot (lower right panel of figure 1). Note that this uncertainty is just a statistical uncertainty of the mtanh fit, which takes into account the variance of experimental data, but does not account for systematic errors in, for example, the relative position of ion and electron temperature profiles or the separatrix position. Hence, it illustrates only part of the total measurement uncertainty, which might be considerably larger.
. The range of gradients spanned by these fits is shown by the shaded areas in the gradient-scale lengths plot (lower right panel of figure 1). Note that this uncertainty is just a statistical uncertainty of the mtanh fit, which takes into account the variance of experimental data, but does not account for systematic errors in, for example, the relative position of ion and electron temperature profiles or the separatrix position. Hence, it illustrates only part of the total measurement uncertainty, which might be considerably larger.

Figure 1. Profiles and gradient-scale length $1/L_X=- X^{-1}\partial X/\partial \rho _{\rm tor}$![]() of ion temperature (orange), electron temperature (blue) and density (green) of AUG 31529 6 ms after the ELM crash. It is assumed that $n_e=n_i$
of ion temperature (orange), electron temperature (blue) and density (green) of AUG 31529 6 ms after the ELM crash. It is assumed that $n_e=n_i$![]() . Data points show experimental measurements (see main text for details), solid lines show the best mtanh fit and dashed lines illustrate alternative mtanh fits within the statistical uncertainty of fit parameters. Grey vertical lines indicate positions where instabilities have been characterised in detail (see § 4).
. Data points show experimental measurements (see main text for details), solid lines show the best mtanh fit and dashed lines illustrate alternative mtanh fits within the statistical uncertainty of fit parameters. Grey vertical lines indicate positions where instabilities have been characterised in detail (see § 4).
We focus on the time point 6 ms after the ELM crash, where the pedestal is mostly recovered and profiles are almost pre-ELM, with a slightly (${\approx }7\,\%$![]() ) reduced electron temperature at the pedestal top. The dashed lines indicate representative positions for pedestal top/shoulder, an intermediate region, pedestal centre and pedestal foot, where linear, local instability scans have been performed (see § 4). With pedestal top/shoulder we refer to the radial position ($\rho _{\rm tor}=0.86$
) reduced electron temperature at the pedestal top. The dashed lines indicate representative positions for pedestal top/shoulder, an intermediate region, pedestal centre and pedestal foot, where linear, local instability scans have been performed (see § 4). With pedestal top/shoulder we refer to the radial position ($\rho _{\rm tor}=0.86$![]() ) just before the increase of temperature and density gradients, where the growth rate spectrum is still clearly distinct from the pedestal centre. Figure 2 shows the $E\times B$
) just before the increase of temperature and density gradients, where the growth rate spectrum is still clearly distinct from the pedestal centre. Figure 2 shows the $E\times B$![]() velocity due to the radial electric field $E_r$
velocity due to the radial electric field $E_r$![]() and the corresponding shear. In figure 3 the radial profiles of further quantities determining edge physics and micro-instabilities are shown: plasma $\beta$
and the corresponding shear. In figure 3 the radial profiles of further quantities determining edge physics and micro-instabilities are shown: plasma $\beta$![]() (strongly falls off from pedestal top to foot), collisionality (strongly increases), the gyroradius (decreases) and the safety factor $q$
(strongly falls off from pedestal top to foot), collisionality (strongly increases), the gyroradius (decreases) and the safety factor $q$![]() (increases but exhibits an intermediate flat region).
(increases but exhibits an intermediate flat region).

Figure 2. The $E\times B$![]() velocity $v_{E_r\times B}=|E_r \times B|/B^2$
velocity $v_{E_r\times B}=|E_r \times B|/B^2$![]() (a) and corresponding shear (b) caused by the edge radial electric field $E_r$
(a) and corresponding shear (b) caused by the edge radial electric field $E_r$![]() .
.

Figure 3. Profiles of further relevant quantities influencing micro-instabilities and edge turbulence: plasma $\beta$![]() (a), collisionality (b), $\rho ^*$
(a), collisionality (b), $\rho ^*$![]() (c) and safety factor $q$
(c) and safety factor $q$![]() combined with magnetic shear $\hat {s}$
combined with magnetic shear $\hat {s}$![]() (d).
(d).
The micro-instabilities that dominate under these physical conditions are characterised with linear, local simulations in the next section.
4 Linear instability characterisation
4.1 Local, linear scans
To characterise the instabilities present in the given pedestal we have performed scans with linear local simulations in the binormal wavenumber $k_y$![]() from $0.05{\rho _i}^{-1}$
from $0.05{\rho _i}^{-1}$![]() to $350{\rho _i}^{-1}$
to $350{\rho _i}^{-1}$![]() (corresponding to e.g. $N_{\rm tor} =[4,29954]$
(corresponding to e.g. $N_{\rm tor} =[4,29954]$![]() at $\rho _{\rm tor}=0.86$
at $\rho _{\rm tor}=0.86$![]() or $N_{\rm tor} = [7,48365]$
or $N_{\rm tor} = [7,48365]$![]() at $\rho _{\rm tor}=0.99$
at $\rho _{\rm tor}=0.99$![]() ), the radial wavenumber at the outboard midplane $k_{x,\text {centre}}$
), the radial wavenumber at the outboard midplane $k_{x,\text {centre}}$![]() from $-$
from $-$![]() 40 to 40 (connected to the ballooning angle $\theta _0=k_{x,\text {centre}}/(\hat {s}k_y)$
40 to 40 (connected to the ballooning angle $\theta _0=k_{x,\text {centre}}/(\hat {s}k_y)$![]() ) and radial position $\rho _{\rm tor}$
) and radial position $\rho _{\rm tor}$![]() from 0.85 to 1. Figure 4 shows the growth rate spectra at four positions (pedestal shoulder, intermediate, pedestal centre and pedestal foot) maximised for each $\rho _{\rm tor}$
from 0.85 to 1. Figure 4 shows the growth rate spectra at four positions (pedestal shoulder, intermediate, pedestal centre and pedestal foot) maximised for each $\rho _{\rm tor}$![]() and $k_y$
and $k_y$![]() over the ballooning angle. At selected wavenumbers, ballooning angles and radial positions we have additionally performed scans in temperature and density gradients ($\pm 30\,\%$
over the ballooning angle. At selected wavenumbers, ballooning angles and radial positions we have additionally performed scans in temperature and density gradients ($\pm 30\,\%$![]() ), collisionality (0–18$\nu ^*_e$
), collisionality (0–18$\nu ^*_e$![]() ) and plasma $\beta$
) and plasma $\beta$![]() (0 %–1 %). In total about 7000 simulations were performed for the characterisation of linear instabilities.
(0 %–1 %). In total about 7000 simulations were performed for the characterisation of linear instabilities.

Figure 4. Growth rate spectra for four radial positions. Here $c_s=\sqrt {T_e/m_i}$![]() and $\rho _i$
and $\rho _i$![]() are local normalisations evaluated at each radial position, and $L_{\rm ref}=0.65$
are local normalisations evaluated at each radial position, and $L_{\rm ref}=0.65$![]() m. Shaded regions indicate the wavenumber ranges used in nonlinear heat flux simulations.
m. Shaded regions indicate the wavenumber ranges used in nonlinear heat flux simulations.
We use the following criteria to distinguish between the different instabilities: parity of the parallel mode structure in ballooning representation (tearing or ballooning), size (ion or electron gyroradius), drift direction (ion or electron diamagnetic), sensitivity on gradients ($T_e$![]() , $T_i$
, $T_i$![]() , $n$
, $n$![]() ), dependence on collisionality and plasma $\beta$
), dependence on collisionality and plasma $\beta$![]() as well as diffusivity and heat flux ratios following the fingerprint approach (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim, Maggi, Giroud, Koechl, Parail, Saarelma, Solano and Chankin2019). An alternative way to identify tearing modes is the tearing or parity factor (see Patel et al. Reference Patel, Dickinson, Roach and Wilson2022), which has been used to verify the identifications. An electromagnetic mode on scales ${>}\rho _i$
as well as diffusivity and heat flux ratios following the fingerprint approach (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim, Maggi, Giroud, Koechl, Parail, Saarelma, Solano and Chankin2019). An alternative way to identify tearing modes is the tearing or parity factor (see Patel et al. Reference Patel, Dickinson, Roach and Wilson2022), which has been used to verify the identifications. An electromagnetic mode on scales ${>}\rho _i$![]() with tearing parity is called MTM. An electromagnetic mode on scales ${>}\rho _i$
with tearing parity is called MTM. An electromagnetic mode on scales ${>}\rho _i$![]() with ballooning parity and drift in ion diamagnetic direction is called KBM. An electrostatic mode on scales ${\approx }\rho _i$
with ballooning parity and drift in ion diamagnetic direction is called KBM. An electrostatic mode on scales ${\approx }\rho _i$![]() , which is stabilised by collisionality and is not destabilised by $\boldsymbol {\nabla } T_i$
, which is stabilised by collisionality and is not destabilised by $\boldsymbol {\nabla } T_i$![]() , is called TEM. An electrostatic mode on scales ${\approx }\rho _i$
, is called TEM. An electrostatic mode on scales ${\approx }\rho _i$![]() , which is destabilised by $\boldsymbol {\nabla } T_i$
, which is destabilised by $\boldsymbol {\nabla } T_i$![]() and propagates in ion diamagnetic direction, is called ITG. An electrostatic mode on scales ${\lessapprox }\rho _i$
and propagates in ion diamagnetic direction, is called ITG. An electrostatic mode on scales ${\lessapprox }\rho _i$![]() that is destabilised by $\boldsymbol {\nabla } T_e$
that is destabilised by $\boldsymbol {\nabla } T_e$![]() is called ETG. However, it should be emphasised that a clear categorisation of modes on ion scales in the region of very strong drive close to the separatrix is particularly challenging. Different drive mechanisms interact and excite instabilities with characteristics that do not fall neatly in the mode prototypes developed in the study of core turbulence.
is called ETG. However, it should be emphasised that a clear categorisation of modes on ion scales in the region of very strong drive close to the separatrix is particularly challenging. Different drive mechanisms interact and excite instabilities with characteristics that do not fall neatly in the mode prototypes developed in the study of core turbulence.
At the pedestal shoulder ($\rho _{\rm tor}=0.86$![]() ; violet triangles in figure 4) we find MTMs on largest scales, TEMs at ion scales, a region of stable wavenumbers and then ETGs on electron scales. In agreement with Kotschenreuther et al. (Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim, Maggi, Giroud, Koechl, Parail, Saarelma, Solano and Chankin2019), the linear TEMs produce significant particle transport ($D_e/(\chi _i+\chi _e)\approx 0.15$
; violet triangles in figure 4) we find MTMs on largest scales, TEMs at ion scales, a region of stable wavenumbers and then ETGs on electron scales. In agreement with Kotschenreuther et al. (Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim, Maggi, Giroud, Koechl, Parail, Saarelma, Solano and Chankin2019), the linear TEMs produce significant particle transport ($D_e/(\chi _i+\chi _e)\approx 0.15$![]() , with particle diffusivity $D$
, with particle diffusivity $D$![]() , heat diffusivity $\chi$
, heat diffusivity $\chi$![]() ) compared with MTMs. At the intermediate position ($\rho _{\rm tor}=0.94$
) compared with MTMs. At the intermediate position ($\rho _{\rm tor}=0.94$![]() ; blue squares in figure 4), where the magnetic shear has a minimum, a growth rate gap without any clear mode on ion scales exists. On intermediate scales, more ETG modes occur, which were not present at the pedestal shoulder. In the steep gradient region ($\rho _{\rm tor}=0.97$
; blue squares in figure 4), where the magnetic shear has a minimum, a growth rate gap without any clear mode on ion scales exists. On intermediate scales, more ETG modes occur, which were not present at the pedestal shoulder. In the steep gradient region ($\rho _{\rm tor}=0.97$![]() ; green crosses in figure 4) on ion scales we find ITG modes that are close to a KBM transition. At smaller scales, ETG-driven modes are present that extend to larger scales towards the pedestal centre and foot. At the pedestal foot ($\rho _{\rm tor}=0.99$
; green crosses in figure 4) on ion scales we find ITG modes that are close to a KBM transition. At smaller scales, ETG-driven modes are present that extend to larger scales towards the pedestal centre and foot. At the pedestal foot ($\rho _{\rm tor}=0.99$![]() ; yellow circles in figure 4) on ion scales modes show an ETG/TEM character but tend to be destabilised with increasing collision frequency. The ETG modes at pedestal centre and foot tend to peak increasingly at finite ballooning angle, indicating the presence of toroidal ETG modes (Told et al. Reference Told, Jenko, Xanthopoulos, Horton and Wolfrum2008; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba, Ball and Ivanov2020). While the fastest-growing ETG modes we find tend to be toroidal in nature, subdominant slab ETGs turn out to play an important role in the nonlinear simulations (see § 5). Overall growth rates increase from pedestal top to foot.
; yellow circles in figure 4) on ion scales modes show an ETG/TEM character but tend to be destabilised with increasing collision frequency. The ETG modes at pedestal centre and foot tend to peak increasingly at finite ballooning angle, indicating the presence of toroidal ETG modes (Told et al. Reference Told, Jenko, Xanthopoulos, Horton and Wolfrum2008; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba, Ball and Ivanov2020). While the fastest-growing ETG modes we find tend to be toroidal in nature, subdominant slab ETGs turn out to play an important role in the nonlinear simulations (see § 5). Overall growth rates increase from pedestal top to foot.
Scans over plasma $\beta$![]() at different radial positions show that the pedestal in these linear local simulations sits close to a KBM threshold – being closer at the pedestal foot than at the pedestal top (cf. figure 5). The closeness to the KBM threshold in the pedestal centre resembles the use of a KBM constraint in the EPED model (Snyder et al. Reference Snyder, Groebner, Leonard, Osborne and Wilson2009) for the prediction of the pedestal width. It has, however, been reported that the radial structure of KBMs may not be compatible with the narrow pedestal region (Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Merlo, Field, Giroud, Hillesheim, Maggi, Perez von Thun, Roach and Saarelma2019; Predebon et al. Reference Predebon, Hatch, Frassinetti, Horvath, Saarelma, Chapman-Oplopoiou, Görler and Maggi2023), suggesting that the details of the KBM threshold may be skewed by the local approximation.
at different radial positions show that the pedestal in these linear local simulations sits close to a KBM threshold – being closer at the pedestal foot than at the pedestal top (cf. figure 5). The closeness to the KBM threshold in the pedestal centre resembles the use of a KBM constraint in the EPED model (Snyder et al. Reference Snyder, Groebner, Leonard, Osborne and Wilson2009) for the prediction of the pedestal width. It has, however, been reported that the radial structure of KBMs may not be compatible with the narrow pedestal region (Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Merlo, Field, Giroud, Hillesheim, Maggi, Perez von Thun, Roach and Saarelma2019; Predebon et al. Reference Predebon, Hatch, Frassinetti, Horvath, Saarelma, Chapman-Oplopoiou, Görler and Maggi2023), suggesting that the details of the KBM threshold may be skewed by the local approximation.

Figure 5. Growth rate scan over plasma $\beta$![]() at $k_y\rho _i=0.075$
at $k_y\rho _i=0.075$![]() and $k_{x,\text {centre}}=0$
and $k_{x,\text {centre}}=0$![]() at four radial positions. Nominal $\beta$
at four radial positions. Nominal $\beta$![]() value indicated in orange.
value indicated in orange.
4.2 Pressure and magnetic shear effect: second stability region
The low growth rates on ion scales in the intermediate region ($\rho _{\rm tor}=0.94$![]() ) between pedestal top and steep gradient are caused by the interplay of low magnetic shear and already increased pressure gradient in this region. Their interplay locally stabilises ballooning modes (second stability region). This can be shown by a scan over the magnetic shear at this position (see figure 6b). At nominal parameters (black crosses) no clear ion-scale mode is present, but with increasing magnetic shear $\hat {s}$
) between pedestal top and steep gradient are caused by the interplay of low magnetic shear and already increased pressure gradient in this region. Their interplay locally stabilises ballooning modes (second stability region). This can be shown by a scan over the magnetic shear at this position (see figure 6b). At nominal parameters (black crosses) no clear ion-scale mode is present, but with increasing magnetic shear $\hat {s}$![]() (green triangles and yellow circles) the system leaves the second stability region and an ion-scale mode becomes unstable. At the pedestal shoulder, where a lot of transport is driven on ion scales, lowering the magnetic shear, unfortunately, does not decrease growth rates significantly, since the pressure gradient is too low to access the second stability region (figure 6a, green triangles). In contrast, a high magnetic shear lets the pedestal shoulder enter the first stability region, where TEMs are suppressed (yellow circles). Further scans with, for example, modified profiles are not within the scope of this paper, but these results illustrate the potential of reducing micro-turbulence instabilities through careful tailoring of safety factor and pressure profiles.
(green triangles and yellow circles) the system leaves the second stability region and an ion-scale mode becomes unstable. At the pedestal shoulder, where a lot of transport is driven on ion scales, lowering the magnetic shear, unfortunately, does not decrease growth rates significantly, since the pressure gradient is too low to access the second stability region (figure 6a, green triangles). In contrast, a high magnetic shear lets the pedestal shoulder enter the first stability region, where TEMs are suppressed (yellow circles). Further scans with, for example, modified profiles are not within the scope of this paper, but these results illustrate the potential of reducing micro-turbulence instabilities through careful tailoring of safety factor and pressure profiles.

Figure 6. Linear, local growth rates as a function of the toroidal mode number $N_{\rm tor}$![]() for three magnetic shear ($\hat {s}$
for three magnetic shear ($\hat {s}$![]() ) values at two different radial positions:(a) pedestal shoulder $\rho _{\rm tor}=0.86$
) values at two different radial positions:(a) pedestal shoulder $\rho _{\rm tor}=0.86$![]() and (b) low-shear region $\rho _{\rm tor}=0.94$
and (b) low-shear region $\rho _{\rm tor}=0.94$![]() . Black crosses are nominal growth rates.
. Black crosses are nominal growth rates.
In the next section, we analyse the nonlinear turbulent system that is driven by the presented instabilities and compare to what extent linear mode signatures prevail in the nonlinear state. To reduce computational cost, ion scales and electron scales are treated separately.
5 Nonlinear heat flux simulations
5.1 Global, ion-scale simulations
To calculate heat fluxes we have performed gradient-driven, global, nonlinear, electromagnetic simulations on ion scales at experimental $\beta$![]() values, which have been enabled by the code upgrade presented in § 2. These simulations cover $\rho _{\rm tor} = 0.85$
values, which have been enabled by the code upgrade presented in § 2. These simulations cover $\rho _{\rm tor} = 0.85$![]() –$0.995$
–$0.995$![]() in radius (almost the full width shown in figure 1) and $k_y\rho _i = 0.05\unicode{x2013}1.6$
in radius (almost the full width shown in figure 1) and $k_y\rho _i = 0.05\unicode{x2013}1.6$![]() in binormal wavenumber (corresponding to a toroidal wavenumber $N_{\rm tor} \approx 4\unicode{x2013}124$
in binormal wavenumber (corresponding to a toroidal wavenumber $N_{\rm tor} \approx 4\unicode{x2013}124$![]() ), indicated by the left shaded region in figure 4. They are two-species simulations (deuterium and electrons) with correct mass ratio ($m_e/m_D=1/3670$
), indicated by the left shaded region in figure 4. They are two-species simulations (deuterium and electrons) with correct mass ratio ($m_e/m_D=1/3670$![]() ), collisions (Landau collision operator) and perpendicular magnetic fluctuations $\bar {A}_{1\parallel }$
), collisions (Landau collision operator) and perpendicular magnetic fluctuations $\bar {A}_{1\parallel }$![]() , but without compressional magnetic perturbations $B_{1,\parallel }$
, but without compressional magnetic perturbations $B_{1,\parallel }$![]() . When indicated, the simulations include the effect of $E\times B$
. When indicated, the simulations include the effect of $E\times B$![]() rotation due to the radial electric field $E_r$
rotation due to the radial electric field $E_r$![]() (cf. figure 2). For numerical reasons the background flow in GENE is restricted to the toroidal direction. As an approximation to the $E\times B$
(cf. figure 2). For numerical reasons the background flow in GENE is restricted to the toroidal direction. As an approximation to the $E\times B$![]() shear effect we retain the magnitude of $v_{E\times B}$
shear effect we retain the magnitude of $v_{E\times B}$![]() , but rotate it to be purely toroidal. In total, the nonlinear global simulations required about $2.5 \times 10^6$
, but rotate it to be purely toroidal. In total, the nonlinear global simulations required about $2.5 \times 10^6$![]() CPUh. More details on, for example, grids are specified in Appendix A.
CPUh. More details on, for example, grids are specified in Appendix A.
The obtained heat fluxes are shown in figure 7 as a function of time averaged over real space (flux surface and radius, including the radial buffer zones; see Appendix A). In both ion and electron channels, the electrostatic heat flux dominates. But while the ions show vanishing electromagnetic heat flux, the electron heat flux is about 1/4 electromagnetic. When including $E\times B$![]() shear in the simulations the heat flux is strongly damped in all channels: the electrostatic heat flux by a factor of three and the electromagnetic heat flux even more strongly.
shear in the simulations the heat flux is strongly damped in all channels: the electrostatic heat flux by a factor of three and the electromagnetic heat flux even more strongly.

Figure 7. Heat fluxes (electrostatic $Q_{\rm es}$![]() and electromagnetic $Q_{\rm em}$
and electromagnetic $Q_{\rm em}$![]() ) for electrons (blue, left) and ions (red, right) as a function of time. The green continuations are performed including an external background velocity shear corresponding to experimentally measured $E\times B$
) for electrons (blue, left) and ions (red, right) as a function of time. The green continuations are performed including an external background velocity shear corresponding to experimentally measured $E\times B$![]() shear.
shear.
5.2 Connecting linear and nonlinear results: frequencies and cross-phases
To identify the dominant turbulent transport mechanisms, results from linear and nonlinear simulations have to be connected, to test if the linearly fastest-growing modes remain important in the nonlinear saturated state. This can be achieved by comparing frequencies and cross-phases.
Figure 8 shows the mode frequencies of the linear and nonlinear simulations. Figure 8(a) shows the frequency spectrum of the local, linear simulations for three radial positions (pedestal shoulder at $\rho _{\rm tor}=0.86$![]() , centre at $\rho _{\rm tor}=0.97$
, centre at $\rho _{\rm tor}=0.97$![]() and foot at $\rho _{\rm tor}=0.99$
and foot at $\rho _{\rm tor}=0.99$![]() ), in the co-moving frame of reference. In the pedestal shoulder spectrum (violet triangles) the transition from MTM to TEM is visible and at the pedestal centre (yellow circles) the transition from ITG to TEM/ETG. Figure 8(b) shows the frequency spectrum of the global, nonlinear simulation analysed at two positions (pedestal shoulder and centre) overlaid by the local, linear spectra. Usually frequencies from local simulations are specified in a frame co-moving with the $E\times B$
), in the co-moving frame of reference. In the pedestal shoulder spectrum (violet triangles) the transition from MTM to TEM is visible and at the pedestal centre (yellow circles) the transition from ITG to TEM/ETG. Figure 8(b) shows the frequency spectrum of the global, nonlinear simulation analysed at two positions (pedestal shoulder and centre) overlaid by the local, linear spectra. Usually frequencies from local simulations are specified in a frame co-moving with the $E\times B$![]() rotation. Since $E\times B$
rotation. Since $E\times B$![]() rotation depends on radial position, frequencies of global simulations are specified in the laboratory frame and for the comparison of both we transform the local frequencies also to the laboratory frame. The comparison shows that at the pedestal shoulder and even at the centre the linear frequencies persist in the nonlinear simulations. This indicates that the linearly fastest-growing modes remain important in the saturated turbulent state. However, one important difference appears. At the pedestal shoulder ($\rho _{\rm tor}=0.86$
rotation depends on radial position, frequencies of global simulations are specified in the laboratory frame and for the comparison of both we transform the local frequencies also to the laboratory frame. The comparison shows that at the pedestal shoulder and even at the centre the linear frequencies persist in the nonlinear simulations. This indicates that the linearly fastest-growing modes remain important in the saturated turbulent state. However, one important difference appears. At the pedestal shoulder ($\rho _{\rm tor}=0.86$![]() ) and $k_y\rho _i\approx 0.3$
) and $k_y\rho _i\approx 0.3$![]() the nonlinear simulation (figure 8b, upper red line) does not show the mode transition that linear, local simulations present (figure 8b, violet triangles). This suggests that MTMs are suppressed or at least restricted to the very largest scales in global, nonlinear simulations compared with the local, linear ones.
the nonlinear simulation (figure 8b, upper red line) does not show the mode transition that linear, local simulations present (figure 8b, violet triangles). This suggests that MTMs are suppressed or at least restricted to the very largest scales in global, nonlinear simulations compared with the local, linear ones.

Figure 8. Frequency spectrum on ion scales for linear, local simulations in the co-moving frame (a) and global, nonlinear results compared with the linear, local scans in the laboratory system (b). The blue colour map (b) shows the distribution of frequencies at two positions from the nonlinear simulations. The red lines are the mean of these distributions. The dashed line in (a) indicates the transition between ion and electron diamagnetic drift direction.
The cross-phases of electric potential and electron density fluctuations (see figure 9) support this picture. Linear mode structures survive in the nonlinear simulations, but on largest scales at the pedestal shoulder differences are visible, corroborating the suppression of MTMs in global, nonlinear simulations observed in the frequency comparison. Overall, the remarkable agreement seen in the frequency and cross-phase comparison between local/linear and global/nonlinear simulations at pedestal shoulder and centre encourages the extension of quasi-linear models to the pedestal region.

Figure 9. Cross-phases of electric potential $\phi$![]() and electron density fluctuations $n$
and electron density fluctuations $n$![]() from nonlinear simulations (blue background) and linear simulations (orange circles).
from nonlinear simulations (blue background) and linear simulations (orange circles).
5.3 Local, electron-scale simulations
Local, nonlinear electron-scale simulations have been performed at multiple radial positions between pedestal top and foot. They complement the global, nonlinear simulations, which only cover ion scales up to $k_y\rho _i = 1.6$![]() at the reference flux surface. The dedicated ETG simulations cover $k_y\rho _i = 2.5\unicode{x2013}157.5$
at the reference flux surface. The dedicated ETG simulations cover $k_y\rho _i = 2.5\unicode{x2013}157.5$![]() (i.e. $k_y\rho _e = 0.04\unicode{x2013}2.6$
(i.e. $k_y\rho _e = 0.04\unicode{x2013}2.6$![]() as indicated by the right shaded region in figure 4). The simulations use adiabatic ions. Resolutions and further simulation settings are given in Appendix A. Figure 10 shows the ETG heat flux obtained in the steep gradient region ($\rho _{\rm tor}=0.97$
as indicated by the right shaded region in figure 4). The simulations use adiabatic ions. Resolutions and further simulation settings are given in Appendix A. Figure 10 shows the ETG heat flux obtained in the steep gradient region ($\rho _{\rm tor}=0.97$![]() ) with nominal profiles and tuned profiles that are designed to increase ETG drive but remain within experimental uncertainties at all locations (see figure 13 in Appendix A). At $\rho _{\rm tor}=0.97$
) with nominal profiles and tuned profiles that are designed to increase ETG drive but remain within experimental uncertainties at all locations (see figure 13 in Appendix A). At $\rho _{\rm tor}=0.97$![]() the tuned profiles have approximately 30 % increased 1/$L_{\rm Te}$
the tuned profiles have approximately 30 % increased 1/$L_{\rm Te}$![]() and 30 % decreased 1/$L_{\rm ne}$
and 30 % decreased 1/$L_{\rm ne}$![]() , resulting in a change of $\eta _e=L_{\rm ne}/L_{\rm Te}$
, resulting in a change of $\eta _e=L_{\rm ne}/L_{\rm Te}$![]() from approximately 1.5 to 3. To make a connection to recent ETG transport scalings for JET and DIII-D (Guttenfelder et al. Reference Guttenfelder, Groebner, Canik, Grierson, Belli and Candy2021; Chapman-Oplopoiou et al. Reference Chapman-Oplopoiou, Hatch, Field, Frassinetti, Hillesheim, Horvath, Maggi, Parisi, Roach, Saarelma and Walker2022; Field et al. Reference Field, Chapman-Oplopoiou, Connor, Frassinetti, Hatch, Roach and Saarelma2023), heat fluxes are shown in modified electron gyro-Bohm units (see figure caption) and megawatts. At nominal parameters the ETG heat flux is very small, whereas with tuned profiles ETGs drive substantial transport of about 0.9 MW. This indicates a strong stiffness of ETG transport in the pedestal centre. By artificially neglecting magnetic drifts in the simulation we can selectively turn off the drive of the toroidal ETG branch to asses the relative importance of slab and toroidal ETG for the heat transport. We find that the pure slab ETG simulation produces slightly less than half of the original transport. This shows that nonlinearly, both slab and toroidal branch contribute substantially to the ETG heat transport in this scenario.
from approximately 1.5 to 3. To make a connection to recent ETG transport scalings for JET and DIII-D (Guttenfelder et al. Reference Guttenfelder, Groebner, Canik, Grierson, Belli and Candy2021; Chapman-Oplopoiou et al. Reference Chapman-Oplopoiou, Hatch, Field, Frassinetti, Hillesheim, Horvath, Maggi, Parisi, Roach, Saarelma and Walker2022; Field et al. Reference Field, Chapman-Oplopoiou, Connor, Frassinetti, Hatch, Roach and Saarelma2023), heat fluxes are shown in modified electron gyro-Bohm units (see figure caption) and megawatts. At nominal parameters the ETG heat flux is very small, whereas with tuned profiles ETGs drive substantial transport of about 0.9 MW. This indicates a strong stiffness of ETG transport in the pedestal centre. By artificially neglecting magnetic drifts in the simulation we can selectively turn off the drive of the toroidal ETG branch to asses the relative importance of slab and toroidal ETG for the heat transport. We find that the pure slab ETG simulation produces slightly less than half of the original transport. This shows that nonlinearly, both slab and toroidal branch contribute substantially to the ETG heat transport in this scenario.

Figure 10. Heat flux due to ETGs at $\rho _{\rm tor}=0.97$![]() as a function of time. Here $L_{\rm ref}=0.65$
as a function of time. Here $L_{\rm ref}=0.65$![]() m, $v_{\rm Te}=\sqrt {2T_e/m_e}$
m, $v_{\rm Te}=\sqrt {2T_e/m_e}$![]() . Left axis in units of modified electron gyro-Bohm units $Q_{{\rm gB},e,{\rm mod}}=Q_{{\rm gB},e}\times 1/{L_{\rm Te}}^2$
. Left axis in units of modified electron gyro-Bohm units $Q_{{\rm gB},e,{\rm mod}}=Q_{{\rm gB},e}\times 1/{L_{\rm Te}}^2$![]() following Chapman-Oplopoiou et al. (Reference Chapman-Oplopoiou, Hatch, Field, Frassinetti, Hillesheim, Horvath, Maggi, Parisi, Roach, Saarelma and Walker2022); right axis in units of megawatts. Parameter $Q_{{\rm gB},e,{\rm mod}}$
following Chapman-Oplopoiou et al. (Reference Chapman-Oplopoiou, Hatch, Field, Frassinetti, Hillesheim, Horvath, Maggi, Parisi, Roach, Saarelma and Walker2022); right axis in units of megawatts. Parameter $Q_{{\rm gB},e,{\rm mod}}$![]() is evaluated at $\rho _{\rm tor}=0.97$
is evaluated at $\rho _{\rm tor}=0.97$![]() for the tuned profiles.
for the tuned profiles.
Figure 11 establishes a connection between the linear and nonlinear ETG simulations by comparing different cross-phases. As expected ETGs do not contribute to particle transport and $\phi \times n = \pi$![]() linearly and nonlinearly. In the potential temperature cross-phases $\phi \times T$
linearly and nonlinearly. In the potential temperature cross-phases $\phi \times T$![]() linear and nonlinear simulations show some resemblance but no clear agreement.
linear and nonlinear simulations show some resemblance but no clear agreement.

Figure 11. Cross-phases of electric potential $\phi$![]() and electron density fluctuations $n$
and electron density fluctuations $n$![]() (a), parallel temperature component (b) and perpendicular temperature component (c) from nonlinear simulations (blue background) and linear simulations (orange circles).
(a), parallel temperature component (b) and perpendicular temperature component (c) from nonlinear simulations (blue background) and linear simulations (orange circles).
5.4 Heat flux profile
To study how turbulent transport changes across the pedestal we consider the heat flux averaged over time and flux surface as a function of the radius. Figure 12 shows important aspects of the turbulent heat flux profile in the studied AUG pedestal. Particular care has to be taken with regard to the normalisation of the heat flux. Due to the strong temperature changes across the pedestal, the commonly used gyro-Bohm heat flux based on mixing-length estimates $Q_{\rm gB}=c_s p_i {\rho ^*}^2=(T_i/m_i)^{1/2}n_iT_i{\rho ^*}^2$![]() changes by two orders of magnitude across the pedestal (figure 12a). A modified gyro-Bohm heat flux $Q_{\rm gb,mod}=Q_{\rm gb}\times \max {(a/L_{\rm Ti},a/L_{\rm Te})}^2$
changes by two orders of magnitude across the pedestal (figure 12a). A modified gyro-Bohm heat flux $Q_{\rm gb,mod}=Q_{\rm gb}\times \max {(a/L_{\rm Ti},a/L_{\rm Te})}^2$![]() , in which the minor radius is replaced by the gradient length as the macroscopic length scale, exhibits strong variations across the pedestal as well. We therefore focus the analysis on the heat flux in SI units.
, in which the minor radius is replaced by the gradient length as the macroscopic length scale, exhibits strong variations across the pedestal as well. We therefore focus the analysis on the heat flux in SI units.

Figure 12. Turbulent heat flux profile in an AUG pedestal from pedestal top to foot. (a) Gyro-Bohm heat flux profile. (b) Components of the ion-scale heat flux profile without $E\times B$![]() shear. (c) Total heat flux ($Q_{\rm es}$
shear. (c) Total heat flux ($Q_{\rm es}$![]() +$Q_{\rm em}$
+$Q_{\rm em}$![]() ) due to ion-scale turbulence with and without $E\times B$
) due to ion-scale turbulence with and without $E\times B$![]() shear. (d) Total heat flux due to ion-scale turbulence from global simulations (red and blue solid lines) as well as ETG heat fluxes from local simulations at nominal values (light blue stars) and increased ETG (dark blue stars) compared with power balance calculations (broad lines). Region of increased measurement uncertainty in grey.
shear. (d) Total heat flux due to ion-scale turbulence from global simulations (red and blue solid lines) as well as ETG heat fluxes from local simulations at nominal values (light blue stars) and increased ETG (dark blue stars) compared with power balance calculations (broad lines). Region of increased measurement uncertainty in grey.

Figure 13. Tuned electron temperature and density profiles (dashed) used to test the sensitivity of ETG heat flux in comparison with nominal profiles (solid).
Figure 12(b) shows the profiles of the different heat flux components (electrostatic, electromagnetic, electron, ion). The dominant component over most of the pedestal is electrostatic electron heat flux (blue solid line), with the exception of $\rho _{\rm tor}\approx 0.97$![]() , where the electrostatic ion heat flux has a local peak. This peak corresponds to the ITG/KBM mode identified in the linear analysis, which occurs at the peak of the ITG. Interestingly, the turbulent ion-scale heat flux is strongly reduced in all channels from pedestal top to pedestal centre and foot – even without $E\times B$
, where the electrostatic ion heat flux has a local peak. This peak corresponds to the ITG/KBM mode identified in the linear analysis, which occurs at the peak of the ITG. Interestingly, the turbulent ion-scale heat flux is strongly reduced in all channels from pedestal top to pedestal centre and foot – even without $E\times B$![]() shear. The onset of this reduction coincides with the region of linear stabilisation, discussed in § 4.2.
shear. The onset of this reduction coincides with the region of linear stabilisation, discussed in § 4.2.
Figure 12(c) illustrates the influence of $E\times B$![]() shear on the heat flux profiles. It reduces the ion-scale heat flux strongly and widens the region of almost vanishing turbulent heat flux.
shear on the heat flux profiles. It reduces the ion-scale heat flux strongly and widens the region of almost vanishing turbulent heat flux.
Figure 12(d) shows that the turbulent heat flux on electron scales behaves oppositely across the pedestal compared with the ion-scale turbulent heat flux. It vanishes at the pedestal top and strongly increases down the pedestal (stars).
A comparison with power balance and neoclassic calculations shows qualitative agreement in heat flux structure and trends (figure 12d). The electron channel is dominant throughout the pedestal. Our gyrokinetic simulations reveal that the electron heat flux transitions in scale. At the pedestal top/shoulder it is driven by ion-scale TEM/MTM turbulence while at the pedestal centre and foot it is driven by small-scale ETG turbulence. While power balance considerations suggest a roughly constant electron heat flux across the pedestal, our gyrokinetic simulations find a reduction towards the pedestal centre. The discrepancy might, for example, be due to $T_i$![]() and $T_e$
and $T_e$![]() profile uncertainties influencing simulations as well as the implicit uncertainties of the interpreted power balance results.
profile uncertainties influencing simulations as well as the implicit uncertainties of the interpreted power balance results.
The region around $\rho _{\rm tor}=0.92$![]() where the total gyrokinetic electron heat flux reaches a minimum likely indicates a limitation of our separate scale ansatz. At this location heat flux is likely driven by scales that are resolved neither in our global simulations nor in the electron-scale simulations (cf. figure 4) and would require multi-scale simulations to be properly resolved. The ion channel contributes substantially to the total heat flux at the pedestal top/shoulder and reduces to neoclassic values towards the pedestal centre. At the pedestal foot our gyrokinetic simulations do not show the increase of ion heat flux suggested by power balance. The differences in the grey-shaded region are possibly due to increased measurement uncertainties in the ion profile that affect both power balance (see Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020) and gyrokinetic simulations.
where the total gyrokinetic electron heat flux reaches a minimum likely indicates a limitation of our separate scale ansatz. At this location heat flux is likely driven by scales that are resolved neither in our global simulations nor in the electron-scale simulations (cf. figure 4) and would require multi-scale simulations to be properly resolved. The ion channel contributes substantially to the total heat flux at the pedestal top/shoulder and reduces to neoclassic values towards the pedestal centre. At the pedestal foot our gyrokinetic simulations do not show the increase of ion heat flux suggested by power balance. The differences in the grey-shaded region are possibly due to increased measurement uncertainties in the ion profile that affect both power balance (see Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020) and gyrokinetic simulations.
For the power balance comparison, the turbulent ion heat flux component was estimated by subtracting neoclassic heat flux calculated with NEOART from the ASTRA result (both from Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020). The total ion heat flux due to power balance is constant (Viezzer et al. Reference Viezzer, Cavedon, Cano-Megias, Fable, Wolfrum, Cruz-Zabala, David, Dux, Fischer, Harrer, Laggner, McDermott, Plank, Pütterich and Willensdorfer2020) and the minimum in the turbulent heat flux is compensated by an increased neoclassic heat flux, which has a roughly constant diffusivity across the pedestal so that its heat flux follows the increasing ITG.
The following picture emerges for the investigated scenario. Turbulent heat flux at the pedestal top is dominated by electrostatic TEMs with electromagnetic MTM contributions. The interplay of low magnetic shear and increasing pressure gradient stabilises modes locally before the steep gradient region ($\rho _{\rm tor}\approx 0.94$![]() ) and reduces turbulent heat flux. The $E\times B$
) and reduces turbulent heat flux. The $E\times B$![]() shear suppresses turbulent heat flux strongly in all channels and widens the region of vanishing turbulent ion-scale heat flux. Turbulent electron heat flux changes scale across the pedestal and turbulent ion heat flux strongly reduces towards the pedestal centre.
shear suppresses turbulent heat flux strongly in all channels and widens the region of vanishing turbulent ion-scale heat flux. Turbulent electron heat flux changes scale across the pedestal and turbulent ion heat flux strongly reduces towards the pedestal centre.
6 Discussion and conclusions
We have presented a gyrokinetic analysis of an AUG ELMy H-mode pedestal. The most unstable micro-instabilities from just inside the pedestal top to foot were characterised with extensive linear, local scans. At the pedestal top/shoulder MTMs, TEMs and ETGs were found. In the intermediate region before the pedestal centre, modes on ion scales are stabilised by the interplay of magnetic shear and pressure gradient, while on intermediate electron scales additional ETG modes become unstable. In the pedestal centre ITG modes close to the threshold to KBMs were observed and at the pedestal foot modes with TEM/ETG character that are destabilised with increasing collision frequency are present. With nonlinear, global, electromagnetic ion-scale simulations and nonlinear, local ETG simulations we have analysed the heat flux in the pedestal – resolved in radius and scale. The ion-scale simulations are enabled by an upgrade of the GENE code (see § 2). We find TEM-driven turbulence with electromagnetic components due to MTMs to be dominant at the pedestal top/shoulder. A combination of linear stabilisation and $E\times B$![]() shear suppresses ion-scale turbulence towards the steep gradient region. While the turbulent electron heat flux is picked up by small-scale ETG modes, the ion channel reduces to neoclassic heat flux levels.
shear suppresses ion-scale turbulence towards the steep gradient region. While the turbulent electron heat flux is picked up by small-scale ETG modes, the ion channel reduces to neoclassic heat flux levels.
The global electromagnetic simulations presented in this study are among the most realistic pedestal turbulence simulations performed to date. Together with dedicated local ETG simulations and the extensive linear instability characterisation, they help to confirm the important role of $E\times B$![]() shear stabilisation for pedestal turbulence and demonstrate the transition in scale of electron turbulence from ion scales at pedestal top to electron scales in the steep gradient region. This well-resolved characterisation of turbulence across a pedestal supports the development of reduced models for edge turbulence and the understanding of the L-mode to H-mode transition.
shear stabilisation for pedestal turbulence and demonstrate the transition in scale of electron turbulence from ion scales at pedestal top to electron scales in the steep gradient region. This well-resolved characterisation of turbulence across a pedestal supports the development of reduced models for edge turbulence and the understanding of the L-mode to H-mode transition.
Two limitations of our current approach should be addressed in future work. First, the separation of ion- and electron-scale simulations prohibits any mutual scale interaction and excludes a range of wavenumbers in our set-up. Several effects have been observed in simulations that include cross-scale interactions. In JET pedestal conditions ion-scale ETGs were found to decrease ETG transport (Parisi et al. Reference Parisi, Parra, Roach, Hardman, Schekochihin, Abel, Aiba, Ball, Barnes, Chapman-Oplopoiou, Dickinson, Dorland, Giroud, Hatch, Hillesheim, Ruiz Ruiz, Saarelma and St-Onge2022) and in DIII-D pedestal top-like conditions an increase of ion-scale and decrease of electron-scale transport were reported (Belli, Candy & Sfiligoi Reference Belli, Candy and Sfiligoi2023). In core conditions a suppression of MTMs by ETG turbulence (Maeyama, Watanabe & Ishizawa Reference Maeyama, Watanabe and Ishizawa2017), a suppression of electron-scale turbulence by ion-scale turbulence and an enhancement of ITGs by electron-scale transport have been found (Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015). Furthermore, an overall increase of turbulent heat fluxes in multi-scale simulations was reported (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016, Reference Howard, Holland, White, Greenwald, Rodriguez-Fernandez, Candy and Creely2018). Overall, these studies suggest that cross-scale interactions may decrease the ETG heat flux we observe by a few 10 %. The second limitation is the use of field-aligned coordinates, which strictly restricts our simulation domain to the region of closed flux surfaces. Approaches that can cross the separatrix would be well suited to expand the study of pedestal foot turbulence.
Acknowledgements
The authors thank E. Viezzer, F. Wilms, S. Makarov, T. Luda di Cortemiglia and B. Chapman-Oplopoiou for fruitful discussions and suggestions. Simulations for this work have been performed on the HPC systems Cobra and Raven at the Max Planck Computing and Data Facility (MPCDF) as well as Marconi at CINECA. Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (grant agreement no. 101052200-EUROfusion).
Declaration of interest
The authors report no conflict of interest.
Data availability
GENE is an open-source code that is freely available via genecode.org upon request. Data and parameter files are available from the corresponding author upon reasonable request.
Appendix A
A.1 Profile variation
Modified profiles were constructed to test the sensitivity of the ETG heat flux on the electron temperature and density profiles. To achieve this, mtanh fit parameters were carefully adjusted to create profiles that remain within experimental uncertainties, but exhibit different gradients. With this approach ETG heat fluxes at multiple locations can be calculated from one consistent profile – an advantage compared to modifying gradients at each radial position separately.
A.2 Simulation parameters
A.2.1 Linear, local simulations
• Two species, experimental $\beta$
 , realistic electron to ion mass ratio $m_e/m_D=1/3670$
, realistic electron to ion mass ratio $m_e/m_D=1/3670$ , Landau collision operator. The $E\times B$
, Landau collision operator. The $E\times B$ shear was not used to avoid Floquet modes.
shear was not used to avoid Floquet modes.• Resolution: $n_x=18$
 , $n_{ky}=1$
, $n_{ky}=1$ , $n_z=36$
, $n_z=36$ , $n_v=32$
, $n_v=32$ , $n_w=16$
, $n_w=16$ .
.• Box size: $lv=3.1$
 , $lw=11$
, $lw=11$ .
.• Convergence tests with increased parallel resolution ($n_z=144$
 ) and increased velocity space resolution ($n_v=128$
) and increased velocity space resolution ($n_v=128$ , $n_w=32$
, $n_w=32$ ) were performed.
) were performed.
A.2.2 Nonlinear, local ETG simulations
• One kinetic species (electrons), adiabatic ions, experimental $\beta$
 , Landau collision operator, no $E\times B$
, Landau collision operator, no $E\times B$ shear.
shear.• Resolution: $n_x=512$
 , $n_{ky}=64$
, $n_{ky}=64$ , $n_z=288$
, $n_z=288$ , $n_v=32$
, $n_v=32$ , $n_w=16$
, $n_w=16$ .
.• Box size: $lv=3$
 , $lw=9$
, $lw=9$ , $lx=3.5$
, $lx=3.5$ .
.• Convergence tests for radial resolution, radial box size and parallel resolution (up to $nz=576$
 ) were performed for the position $rho_{\rm tor}=0.97$
) were performed for the position $rho_{\rm tor}=0.97$ .
.
A.2.3 Nonlinear, global, ion-scale simulations
• Two species, experimental $\beta$
 , realistic electron to ion mass ratio $m_e/m_D=1/3670$
, realistic electron to ion mass ratio $m_e/m_D=1/3670$ , Landau collision operator. With $E\times B$
, Landau collision operator. With $E\times B$ shear when indicated.
shear when indicated.• Resolution: $n_x=512$
 , $n_{ky}=32$
, $n_{ky}=32$ , $n_z=48$
, $n_z=48$ , $n_v=32$
, $n_v=32$ , $n_w=16$
, $n_w=16$ .
.• Box size: $lv=3.45$
 , $lw=14.23$
, $lw=14.23$ , $lx=72$
, $lx=72$ .
.• Boundary conditions: Dirichlet with radial buffer zones (5 % of domain at both boundaries), in which the distribution function is damped by fourth-order Krook operators.
• Performed with block-structured velocity grids (Jarema et al. Reference Jarema, Bungartz, Görler, Jenko, Neckel and Told2017) with 4 blocks.
• Performed in single-precision floating-point format.
A.2.4 Definitions
• $lv$
 is the extension of the simulation box in the $v_{||}$
is the extension of the simulation box in the $v_{||}$ direction, in units of the thermal velocity $v_T = (2T_0/m)^{1/2}$
direction, in units of the thermal velocity $v_T = (2T_0/m)^{1/2}$ .
.• $lw$
 is the extension of the simulation box in the $\mu$
is the extension of the simulation box in the $\mu$ direction, in units of $T_0/B_{\rm ref}$
direction, in units of $T_0/B_{\rm ref}$ .
.• $lx$
 is the extension of the simulations box in the radial direction in units of the gyroradius.
is the extension of the simulations box in the radial direction in units of the gyroradius.