Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T13:24:55.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Collisionless distribution functions for force-free current sheets: using a pressure transformation to lower the plasma beta

Published online by Cambridge University Press:  14 June 2018

F. Wilson Open the ORCID record for F. Wilson [Opens in a new window] ,
T. Neukirch Open the ORCID record for T. Neukirch [Opens in a new window]  and
O. Allanson Open the ORCID record for O. Allanson [Opens in a new window]
F. Wilson*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
T. Neukirch
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
O. Allanson
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK Space and Atmospheric Electricity Group, Department of Meteorology, University of Reading, Reading RG6 6BB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

So far, only one distribution function giving rise to a collisionless nonlinear force-free current sheet equilibrium allowing for a plasma beta less than one is known (Allanson et al., Phys. Plasmas, vol. 22 (10), 2015, 102116; Allanson et al., J. Plasma Phys., vol. 82 (3), 2016a, 905820306). This distribution function can only be expressed as an infinite series of Hermite functions with very slow convergence and this makes its practical use cumbersome. It is the purpose of this paper to present a general method that allows us to find distribution functions consisting of a finite number of terms (therefore easier to use in practice), but which still allow for current sheet equilibria that can, in principle, have an arbitrarily low plasma beta. The method involves using known solutions and transforming them into new solutions using transformations based on taking integer powers ($N$) of one component of the pressure tensor. The plasma beta of the current sheet corresponding to the transformed distribution functions can then, in principle, have values as low as 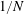$1/N$. We present the general form of the distribution functions for arbitrary $N$ and then, as a specific example, discuss the case for $N=2$ in detail.

Keywords

astrophysical plasmasspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 3 , June 2018 , 905840309
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham-Shrauner, B. 2013 Force-free Jacobian equilibria for Vlasov–Maxwell plasmas. Phys. Plasmas 20 (10), 102117.CrossRefGoogle Scholar
Akcay, C., Daughton, W., Lukin, V. S. & Liu, Y.-H. 2016 A two-fluid study of oblique tearing modes in a force-free current sheet. Phys. Plasmas 23 (1), 012112.Google Scholar
Allanson, O.2017 Theory of one-dimensional Vlasov–Maxwell equilibria: with applications to collisionless current sheets and flux tubes. PhD Thesis, University of St Andrews. arXiv:1710.01348.Google Scholar
Allanson, O., Neukirch, T., Troscheit, S. & Wilson, F. 2016a From one-dimensional fields to Vlasov equilibria: theory and application of Hermite polynomials. J. Plasma Phys. 82 (3), 905820306.CrossRefGoogle Scholar
Allanson, O., Neukirch, T., Wilson, F. & Troscheit, S. 2015 An exact collisionless equilibrium for the force-free Harris sheet with low plasma beta. Phys. Plasmas 22 (10), 102116.Google Scholar
Allanson, O., Troscheit, S. & Neukirch, T. 2018 On the inverse problem for Channell collisionless plasma equilibria. IMA J. Appl. Math. 00, 1–25.Google Scholar
Allanson, O., Wilson, F. & Neukirch, T. 2016b Neutral and non-neutral collisionless plasma equilibria for twisted flux tubes: the gold-hoyle model in a background field. Phys. Plasmas 23 (9), 092106.Google Scholar
Alpers, W. 1969 Steady state charge neutral models of the magnetopause. Astrophys. Space Sci. 5, 425–437.CrossRefGoogle Scholar
Artemyev, A. V. 2011 A model of one-dimensional current sheet with parallel currents and normal component of magnetic field. Phys. Plasmas 18 (2), 022104.Google Scholar
Artemyev, A. V., Angelopoulos, V., Halekas, J. S., Runov, A., Zelenyi, L. M. & McFadden, J. P. 2017a Mars’s magnetotail: nature’s current sheet laboratory. J. Geophys. Res. pp. n/a–n/a, 2017JA024078.Google Scholar
Artemyev, A. V., Angelopoulos, V., Liu, J. & Runov, A. 2017b Electron currents supporting the near-earth magnetotail during current sheet thinning. Geophys. Res. Lett. 44, 5–11.CrossRefGoogle Scholar
Artemyev, A. V., Vasko, I. Y. & Kasahara, S. 2014 Thin current sheets in the Jovian magnetotail. Planet. Space Sci. 96, 133–145.Google Scholar
Attico, N. & Pegoraro, F. 1999 Periodic equilibria of the Vlasov–Maxwell system. Phys. Plasmas 6, 767–770.Google Scholar
Bobrova, N. A., Bulanov, S. V., Sakai, J. I. & Sugiyama, D. 2001 Force-free equilibria and reconnection of the magnetic field lines in collisionless plasma configurations. Phys. Plasmas 8, 759–768.Google Scholar
Bobrova, N. A., Bulanov, S. V., Vekstein, G. E., Sakai, J.-I., Machida, K. & Haruki, T. 2003 Tearing instability of a force-free magnetic configuration in a collisionless plasma. Plasma Phys. Rep. 29, 449–458.Google Scholar
Bobrova, N. A. & Syrovatskiǐ, S. I. 1979 Violent instability of one-dimensional forceless magnetic field in a rarefied plasma. Sov. J. Exp. Theor. Phys. Lett. 30, 535.Google Scholar
Borissov, A., Kontar, E. P., Threlfall, J. & Neukirch, T. 2017 Particle acceleration with anomalous pitch angle scattering in 2d magnetohydrodynamic reconnection simulations. Astron. Astrophys. 605, A73.Google Scholar
Bowers, K. & Li, H. 2007 Spectral energy transfer and dissipation of magnetic energy from fluid to kinetic scales. Phys. Rev. Lett. 98 (3), 035002.CrossRefGoogle ScholarPubMed
Burgess, D., Gingell, P. W. & Matteini, L. 2016 Multiple current sheet systems in the outer heliosphere: energy release and turbulence. Astrophys. J. 822, 38.Google Scholar
Channell, P. J. 1976 Exact Vlasov–Maxwell equilibria with sheared magnetic fields. Phys. Fluids 19, 1541–1545.CrossRefGoogle Scholar
Correa-Restrepo, D. & Pfirsch, D. 1993 Negative-energy waves in an inhomogeneous force-free Vlasov plasma with sheared magnetic field. Phys. Rev. E 47, 545–563.Google Scholar
Dorville, N., Belmont, G., Aunai, N., Dargent, J. & Rezeau, L. 2015 Asymmetric kinetic equilibria: generalization of the bas model for rotating magnetic profile and non-zero electric field. Phys. Plasmas 22 (9), 092904.Google Scholar
Fan, F., Huang, C., Lu, Q., Xie, J. & Wang, S. 2016 The structures of magnetic islands formed during collisionless magnetic reconnections in a force-free current sheet. Phys. Plasmas 23 (11), 112106.Google Scholar
Gingell, I., Sorriso-Valvo, L., Burgess, D., de Vita, G. & Matteini, L. 2017 Three-dimensional simulations of sheared current sheets: transition to turbulence? J. Plasma Phys. 83 (1), 705830104.Google Scholar
Guo, F., Li, H., Daughton, W., Li, X. & Liu, Y.-H. 2016b Particle acceleration during magnetic reconnection in a low-beta pair plasma. Phys. Plasmas 23 (5), 055708.CrossRefGoogle Scholar
Guo, F., Li, H., Daughton, W. & Liu, Y.-H. 2014 Formation of hard power laws in the energetic particle spectra resulting from relativistic magnetic reconnection. Phys. Rev. Lett. 113, 155005.Google Scholar
Guo, F., Li, X., Li, H., Daughton, W., Zhang, B., Lloyd-Ronning, N., Liu, Y.-H., Zhang, H. & Deng, W. 2016a Efficient production of high-energy nonthermal particles during magnetic reconnection in a magnetically dominated ion-electron plasma. Astrophys. J. Lett. 818, L9.CrossRefGoogle Scholar
Guo, F., Liu, Y.-H., Daughton, W. & Li, H. 2015 Particle acceleration and plasma dynamics during magnetic reconnection in the magnetically dominated regime. Astrophys. J. 806, 167.CrossRefGoogle Scholar
Harrison, M. G. & Neukirch, T. 2009a One-dimensional Vlasov–Maxwell equilibrium for the force-free Harris sheet. Phys. Rev. Lett. 102 (13), 135003.Google Scholar
Harrison, M. G. & Neukirch, T. 2009b Some remarks on one-dimensional force-free Vlasov–Maxwell equilibria. Phys. Plasmas 16 (2), 022106.CrossRefGoogle Scholar
Hesse, M., Kuznetsova, M., Schindler, K. & Birn, J. 2005 Three-dimensional modeling of electron quasiviscous dissipation in guide-field magnetic reconnection. Phys. Plasmas 12 (10), 100704.Google Scholar
Huang, F., Xu, J., Yan, F., Zhang, M. & Yu, M. Y. 2017 Instabilities of current-sheet with a nonuniform guide field. Phys. Plasmas 24 (9), 092104.Google Scholar
Kivelson, M. G. & Khurana, K. K. 1995 Models of flux ropes embedded in a Harris neutral sheet: force-free solutions in low and high beta plasmas. J. Geophys. Res. 100, 23637–23646.Google Scholar
Kolotkov, D. Y., Vasko, I. Y. & Nakariakov, V. M. 2015 Kinetic model of force-free current sheets with non-uniform temperature. Phys. Plasmas 22 (11), 112902.Google Scholar
Krall, N. A. & Trivelpiece, A. W. 1973 Principles of Plasma Physics, International Student Edition – International Series in Pure and Applied Physics. McGraw-Hill Kogakusha.Google Scholar
Liu, Y.-H., Daughton, W., Karimabadi, H., Li, H. & Roytershteyn, V. 2013 Bifurcated structure of the electron diffusion region in three-dimensional magnetic reconnection. Phys. Rev. Lett. 110, 265004.CrossRefGoogle ScholarPubMed
Lukin, A., Vasko, I., Artemyev, A. & Yushkov, E. 2018 Two-dimensional self-similar plasma equilibria. Phys. Plasmas 25 (1), 012906.CrossRefGoogle Scholar
Marsh, G. 1996 Force-Free Magnetic Fields: Solutions, Topology and Applications. World Scientific.CrossRefGoogle Scholar
Moratz, E. & Richter, E. W. 1966 Elektronen-Geschwindigkeitsverteilungsfunktionen für kraftfreie bzw. teilweise kraftfreie Magnetfelder. Z. Naturforsch. A 21, 1963.CrossRefGoogle Scholar
Neukirch, T., Wilson, F. & Allanson, O. 2018 Collisionless current sheet equilibria. Plasma Phys. Control. Fusion 60 (1), 014008.CrossRefGoogle Scholar
Neukirch, T., Wilson, F. & Harrison, M. G. 2009 A detailed investigation of the properties of a Vlasov–Maxwell equilibrium for the force-free Harris sheet. Phys. Plasmas 16 (12), 122102.CrossRefGoogle Scholar
Nishimura, K., Gary, S. P., Li, H. & Colgate, S. A. 2003 Magnetic reconnection in a force-free plasma: simulations of micro- and macroinstabilities. Phys. Plasmas 10, 347–356.Google Scholar
Panov, E. V., Artemyev, A. V., Nakamura, R. & Baumjohann, W. 2011 Two types of tangential magnetopause current sheets: cluster observations and theory. J. Geophys. Res. (Space Phys.) 116, A12204.Google Scholar
Priest, E. 2014 Magnetohydrodynamics of the Sun. Cambridge University Press.Google Scholar
Pritchett, P. L. & Coroniti, F. V. 2004 Three-dimensional collisionless magnetic reconnection in the presence of a guide field. J. Geophys. Res. (Space Phys.) 109, 1220.Google Scholar
Schindler, K. 2007 Physics of Space Plasma Activity. Cambridge University Press.Google Scholar
Sestero, A. 1967 Self-consistent description of a warm stationary plasma in a uniformly sheared magnetic field. Phys. Fluids 10, 193–197.Google Scholar
Stark, C. R. & Neukirch, T. 2012 Collisionless distribution function for the relativistic force-free Harris sheet. Phys. Plasmas 19 (1), 012115.Google Scholar
Tassi, E., Pegoraro, F. & Cicogna, G. 2008 Solutions and symmetries of force-free magnetic fields. Phys. Plasmas 15 (9), 092113.CrossRefGoogle Scholar
Vasko, I. Y., Artemyev, A. V., Petrukovich, A. A. & Malova, H. V. 2014 Thin current sheets with strong bell-shape guide field: cluster observations and models with beams. Ann. Geophys. 32, 1349–1360.Google Scholar
Vekstein, G. E., Bobrova, N. A. & Bulanov, S. V. 2002 On the motion of charged particles in a sheared force-free magnetic field. J. Plasma Phys. 67, 215–221.Google Scholar
Vinogradov, A. A., Vasko, I. Y., Artemyev, A. V., Yushkov, E. V., Petrukovich, A. A. & Zelenyi, L. M. 2016 Kinetic models of magnetic flux ropes observed in the earth magnetosphere. Phys. Plasmas 23 (7), 072901.Google Scholar
Wiegelmann, T. & Sakurai, T. 2012 Solar force-free magnetic fields. Living Rev. Solar Phys. 9 (1), 5.CrossRefGoogle Scholar
Wilson, F.2012 Equilibrium and stability properties of collisionless current sheet models. PhD thesis, School of Mathematics and Statistics, University of St. Andrews, North Haugh, St Andrews KY16 9SS.Google Scholar
Wilson, F. & Neukirch, T. 2011 A family of one-dimensional Vlasov–Maxwell equilibria for the force-free Harris sheet. Phys. Plasmas 18, 082108.Google Scholar
Wilson, F., Neukirch, T. & Allanson, O. 2017 Force-free collisionless current sheet models with non-uniform temperature and density profiles. Phys. Plasmas 24 (9), 092105.Google Scholar
Wilson, F., Neukirch, T., Hesse, M., Harrison, M. G. & Stark, C. R. 2016 Particle-in-cell simulations of collisionless magnetic reconnection with a non-uniform guide field. Phys. Plasmas 23 (3), 032302.Google Scholar
Wolf, K. B. 1977 On self-reciprocal functions under a class of integral transforms. J. Math. Phys. 18 (5), 1046–1051.CrossRefGoogle Scholar
Zelenyi, L. M., Frank, A. G., Artemyev, A. V., Petrukovich, A. A. & Nakamura, R. 2016 Formation of sub-ion scale filamentary force-free structures in the vicinity of reconnection region. Plasma Phys. Control. Fusion 58 (5), 054002.CrossRefGoogle Scholar
Zhou, F., Huang, C., Lu, Q., Xie, J. & Wang, S. 2015 The evolution of the ion diffusion region during collisionless magnetic reconnection in a force-free current sheet. Phys. Plasmas 22 (9), 092110.Google Scholar