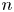1. Introduction
The stability properties of ideal and resistive modes are strongly influenced by kinetic effects (diamagnetic effects, viscosity, etc.). However, these effects are not included in the widely used simplified ideal or resistive fluid moment equations. Expressing the kinetic effects in terms of low-order fluid moments and including them in the fluid moment equations, the resulting extended equations describe both fluid and kinetic features (Chang & Callen Reference Chang and Callen1992). Depending on the plasma properties, various sets of fluid equations (Mikhailovskii Reference Mikhailovskii1998; Huysmans et al. Reference Huysmans, Sharapov, Mikhailovskii and Kerner2001; Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006; Aiba Reference Aiba2016) and approximations of viscous stress tensor $\boldsymbol {\nabla } \boldsymbol {\cdot} {\varPi }$![]() and heat flux $\boldsymbol {q}$
and heat flux $\boldsymbol {q}$![]() (Chang & Callen Reference Chang and Callen1992) have been established within the framework of magnetohydrodynamics (MHD). Drift MHD equations are used in linear (e.g. MISHKA-D (Huysmans et al. Reference Huysmans, Sharapov, Mikhailovskii and Kerner2001), MISHKA-F (Chapman et al. Reference Chapman, Sharapov, Huysmans and Mikhailovskii2006), MINERVA-DI (Aiba Reference Aiba2016)) and nonlinear (e.g. JOREK (Hoelzl et al. Reference Hoelzl, Huijsmans, Pamela, Bécoulet, Nardon, Artola, Nkonga, Atanasiu, Bandaru and Bhole2021), XTOR-2F (Lütjens & Luciani Reference Lütjens and Luciani2010)) codes to investigate diamagnetic drift effects. These codes differ in the applied numerical methods and in the detailed form of the extended MHD equations.
(Chang & Callen Reference Chang and Callen1992) have been established within the framework of magnetohydrodynamics (MHD). Drift MHD equations are used in linear (e.g. MISHKA-D (Huysmans et al. Reference Huysmans, Sharapov, Mikhailovskii and Kerner2001), MISHKA-F (Chapman et al. Reference Chapman, Sharapov, Huysmans and Mikhailovskii2006), MINERVA-DI (Aiba Reference Aiba2016)) and nonlinear (e.g. JOREK (Hoelzl et al. Reference Hoelzl, Huijsmans, Pamela, Bécoulet, Nardon, Artola, Nkonga, Atanasiu, Bandaru and Bhole2021), XTOR-2F (Lütjens & Luciani Reference Lütjens and Luciani2010)) codes to investigate diamagnetic drift effects. These codes differ in the applied numerical methods and in the detailed form of the extended MHD equations.
We upgrade the three-dimensional (3-D) linear resistive stability CASTOR3D code (Strumberger & Günter Reference Strumberger and Günter2017, Reference Strumberger and Günter2019) by taking into account gyro-viscosity in the momentum equation, as well as pressure and Hall terms in Ohm's law. Including additional physical effects in linear MHD equations may lead to so-called ‘parasitic’ solutions which make it difficult to find and identify physically meaningful solutions. Besides a high numerical accuracy (high-quality equilibrium input, radial resolution, etc.) the analytical reduction of the model offers a possibility to reduce the occurrence of ‘parasitic’ modes (Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006). We therefore make use of the drift approximation and implement the resulting simplified version of Ohm's law. This reduces the numerical problems and eliminates the Whistler waves.
The ion and electron diamagnetic drift effects caused by the newly implemented terms are investigated for ideal and resistive, low- and medium-$n$![]() internal modes of two-dimensional (2-D) and 3-D high-$\beta$
internal modes of two-dimensional (2-D) and 3-D high-$\beta$![]() and 2-D low-$\beta$
and 2-D low-$\beta$![]() test equilibria. The types of these modes are specified more precisely by analysing the corresponding ideal or resistive energy functional that is determined from the solution of the eigenvalue problem without diamagnetic drift effects (Puchmayr, Dunne & Strumberger Reference Puchmayr, Dunne and Strumberger2022). The diamagnetic drift effects are studied for ideal modes of the axisymmetric high-$\beta$
test equilibria. The types of these modes are specified more precisely by analysing the corresponding ideal or resistive energy functional that is determined from the solution of the eigenvalue problem without diamagnetic drift effects (Puchmayr, Dunne & Strumberger Reference Puchmayr, Dunne and Strumberger2022). The diamagnetic drift effects are studied for ideal modes of the axisymmetric high-$\beta$![]() equilibrium and resistive modes of the corresponding low-$\beta$
equilibrium and resistive modes of the corresponding low-$\beta$![]() equilibrium. The obtained results confirm the previous finding that diamagnetic drift effects may damp or even stabilise the modes (e.g. Aiba Reference Aiba2016). Moreover, we investigate the diamagnetic drift effects depending on various ratios of ion and electron pressures. The results indicate that the often used assumptions $p_i=p_e$
equilibrium. The obtained results confirm the previous finding that diamagnetic drift effects may damp or even stabilise the modes (e.g. Aiba Reference Aiba2016). Moreover, we investigate the diamagnetic drift effects depending on various ratios of ion and electron pressures. The results indicate that the often used assumptions $p_i=p_e$![]() (equal pressures) or $p=p_e, p_i=0$
(equal pressures) or $p=p_e, p_i=0$![]() (cold ions) (e.g. Lütjens & Luciani Reference Lütjens and Luciani2010; Aiba Reference Aiba2016; Pamela et al. Reference Pamela, Bhole, Huijsmans, Nkonga, Hoelzl, Krebs and Strumberger2020) may not always be a good approximation.
(cold ions) (e.g. Lütjens & Luciani Reference Lütjens and Luciani2010; Aiba Reference Aiba2016; Pamela et al. Reference Pamela, Bhole, Huijsmans, Nkonga, Hoelzl, Krebs and Strumberger2020) may not always be a good approximation.
Usually, 3-D linear stability codes (e.g. CAS3D (Nührenberg Reference Nührenberg1996), TERPSICHORE (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990), etc.) are restricted to purely ideal stability studies. The CASTOR3D code, however, is a 3-D linear stability code which takes into account important physical effects just as 2-D linear stability codes (e.g. MARS (Chu et al. Reference Chu, Greene, Jensen, Miller, Bondeson, Johnson and Mauel1995), MISHKA-D (Huysmans et al. Reference Huysmans, Sharapov, Mikhailovskii and Kerner2001), MISHKA-F (Chapman et al. Reference Chapman, Sharapov, Huysmans and Mikhailovskii2006), MINERVA-DI (Aiba Reference Aiba2016), etc.). Considering a 3-D high-$\beta$![]() test equilibrium with helical core, we investigate the ion diamagnetic drift effect on low-$n^*$
test equilibrium with helical core, we investigate the ion diamagnetic drift effect on low-$n^*$![]() internal modes, with $n^*$
internal modes, with $n^*$![]() indicating the global mode structure. In many cases $n^*$
indicating the global mode structure. In many cases $n^*$![]() corresponds to the dominant toroidal Fourier harmonic contributing to the mode (Strumberger & Günter Reference Strumberger and Günter2019). The results are compared with those obtained for the corresponding axisymmetric equilibrium.
corresponds to the dominant toroidal Fourier harmonic contributing to the mode (Strumberger & Günter Reference Strumberger and Günter2019). The results are compared with those obtained for the corresponding axisymmetric equilibrium.
In § 2 we present the extended MHD equations (§ 2.1) and their linearised forms which have been implemented in the CASTOR3D code (§ 2.2). The diamagnetic drift effects of these additional terms are investigated for ideal internal modes (§ 3.1) and resistive internal modes (§ 3.2) of the corresponding axisymmetric equilibria. Stability studies for the ideal internal modes of the 3-D equilibrium are the subject of § 3.3. In § 4 a summary of the results and an outlook on further studies are given. Finally, a simplified computation of the drift frequencyand a discussion of the numerical accuracy of the CASTOR3D results are presented in Appendices A and B, respectively.
2. Theory
2.1. Extended MHD equations
The upgraded version of the linear stability CASTOR3D code, which is used for the presented computations, is based on the extended MHD equations (Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006):
They correspond to the generally used single-fluid equations (e.g. Huysmans, Goedbloed & Kerner Reference Huysmans, Goedbloed and Kerner1993) plus additional two-fluid terms. These equations are derived from the two-fluid MHD equations (Braginskii Reference Braginskii1965) making several assumptions and approximations, e.g. assuming quasi-neutrality $n=n_i=n_e$![]() ($n_i$
($n_i$![]() is ion density, $n_e$
is ion density, $n_e$![]() is electron density), neglecting the electron mass ($m_i > > m_e$
is electron density), neglecting the electron mass ($m_i > > m_e$![]() , mass density $\rho = m_i n + m_e n \approx m_i n$
, mass density $\rho = m_i n + m_e n \approx m_i n$![]() ), using pressure $p=p_i+p_e=n(T_i+T_e)=nT$
), using pressure $p=p_i+p_e=n(T_i+T_e)=nT$![]() ($T_i$
($T_i$![]() is ion temperature, $T_e$
is ion temperature, $T_e$![]() is electron temperature, $T=T_i+T_e$
is electron temperature, $T=T_i+T_e$![]() ) and making the velocity approximation ${\boldsymbol V}={m_i {\boldsymbol V}_i + m_e {\boldsymbol V}_e}/{m_i+m_e}\approx {\boldsymbol V}_i$
) and making the velocity approximation ${\boldsymbol V}={m_i {\boldsymbol V}_i + m_e {\boldsymbol V}_e}/{m_i+m_e}\approx {\boldsymbol V}_i$![]() , with ${\boldsymbol V}_i$
, with ${\boldsymbol V}_i$![]() being the ion velocity. The set of equations is closed with the Maxwell equations
being the ion velocity. The set of equations is closed with the Maxwell equations
(${\boldsymbol E}$![]() is electric field, ${\boldsymbol B}$
is electric field, ${\boldsymbol B}$![]() is magnetic field, ${\boldsymbol j}$
is magnetic field, ${\boldsymbol j}$![]() is current density), where $\mu _0 \epsilon _0 ({\partial {\boldsymbol E}}/{\partial t})$
is current density), where $\mu _0 \epsilon _0 ({\partial {\boldsymbol E}}/{\partial t})$![]() is neglected. The ion velocity ${\boldsymbol V}_i$
is neglected. The ion velocity ${\boldsymbol V}_i$![]() is given by
is given by

There, ${\boldsymbol V}_{{\rm MHD}} = {\boldsymbol V}_E + {\boldsymbol V}_{||}$![]() is the so-called MHD velocity, ${\boldsymbol V}_i^*$
is the so-called MHD velocity, ${\boldsymbol V}_i^*$![]() is the ion diamagnetic drift velocity and $\alpha ={m_i}/{e}$
is the ion diamagnetic drift velocity and $\alpha ={m_i}/{e}$![]() , with $e$
, with $e$![]() being the elementary charge. Additionally to the ideal MHD equations, the extended MHD equations take into account the viscous force density $-{\boldsymbol {\nabla }} \boldsymbol {\cdot } { \varPi }$
being the elementary charge. Additionally to the ideal MHD equations, the extended MHD equations take into account the viscous force density $-{\boldsymbol {\nabla }} \boldsymbol {\cdot } { \varPi }$![]() in the momentum equation (2.2), as well as the electron pressure-gradient term $({m_i}/{e\rho }) {\boldsymbol {\nabla }} p_e$
in the momentum equation (2.2), as well as the electron pressure-gradient term $({m_i}/{e\rho }) {\boldsymbol {\nabla }} p_e$![]() , the Hall term $({m_i}/{e\rho }) {\bf j} \times {\boldsymbol B}$
, the Hall term $({m_i}/{e\rho }) {\bf j} \times {\boldsymbol B}$![]() and the plasma resistivity term $\eta {\boldsymbol j}$
and the plasma resistivity term $\eta {\boldsymbol j}$![]() in the extended Ohm's law (2.4). The viscous stress tensor $\varPi$
in the extended Ohm's law (2.4). The viscous stress tensor $\varPi$![]() splits into ${ \varPi } = { \varPi }_{||} + { \varPi }_{\wedge } + { \varPi }_{\perp }$
splits into ${ \varPi } = { \varPi }_{||} + { \varPi }_{\wedge } + { \varPi }_{\perp }$![]() , with parallel ${ \varPi }_{||}$
, with parallel ${ \varPi }_{||}$![]() , cross (gyro-viscous) ${ \varPi }_{\wedge }$
, cross (gyro-viscous) ${ \varPi }_{\wedge }$![]() , and perpendicular ${ \varPi }_{\perp }$
, and perpendicular ${ \varPi }_{\perp }$![]() parts. We already introduced the approximation
parts. We already introduced the approximation
in the previous CASTOR3D version (Strumberger & Günter Reference Strumberger and Günter2019), while the perpendicular viscosity is not implemented in the code. The parallel viscosity coefficient $\mu _{||}$![]() is an input parameter. However, in this work we neglect the parallel viscosity ($\mu _{||}=0$
is an input parameter. However, in this work we neglect the parallel viscosity ($\mu _{||}=0$![]() ), and concentrate our studies on the diamagnetic drift effects. The gyro-viscous force is approximated by (Chang & Callen Reference Chang and Callen1992)
), and concentrate our studies on the diamagnetic drift effects. The gyro-viscous force is approximated by (Chang & Callen Reference Chang and Callen1992)
This expression is generally known as gyro-viscous cancellation. Using (2.7) and (2.8), the momentum equation (2.2) reduces to
The extended Ohm's law (2.4) is simplified by using the drift approximation of the Hall term (Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006):
which leads to
and eliminates the Whistler waves.
As already mentioned, single-fluid codes that include two-fluid effects often use the assumption $p_i=p_e=0.5p$![]() , that is, $T_i=T_e$
, that is, $T_i=T_e$![]() . However, measured ion and electron temperatures may be different. Therefore, we use the ansatz
. However, measured ion and electron temperatures may be different. Therefore, we use the ansatz
with $0\le \alpha _T \le 1$![]() . The parameter $\alpha _T$
. The parameter $\alpha _T$![]() provides an additional degree of freedom that allows one to choose a more realistic ratio of ion and electron pressures with respect to the measured temperatures, that is, a more realistic treatment of ion and electron diamagnetic drift effects. Application of (2.12a,b) to the ion drift velocity (2.6) and the pressure terms of (2.11) yields
provides an additional degree of freedom that allows one to choose a more realistic ratio of ion and electron pressures with respect to the measured temperatures, that is, a more realistic treatment of ion and electron diamagnetic drift effects. Application of (2.12a,b) to the ion drift velocity (2.6) and the pressure terms of (2.11) yields
and the simplified Ohm's law
with ${\boldsymbol {\nabla }}_{||}p =({1}/{B^2}){\boldsymbol B} ({\boldsymbol B} \boldsymbol {\cdot } {\boldsymbol {\nabla }} p)$![]() .
.
Equations (2.1), (2.9), (2.3) and (2.14) of the standard drift model are only valid in the drift ordering, that is, $\epsilon \thicksim \delta ^2$![]() and $\xi \thicksim \delta$
and $\xi \thicksim \delta$![]() with $\epsilon =\omega /\varOmega _i$
with $\epsilon =\omega /\varOmega _i$![]() ($\omega$
($\omega$![]() is characteristic frequency, $\varOmega _i$
is characteristic frequency, $\varOmega _i$![]() is ion gyro-frequency), $\xi =V_0/V_{thi}$
is ion gyro-frequency), $\xi =V_0/V_{thi}$![]() ($V_0$
($V_0$![]() is characteristic flow velocity, $V_{thi}$
is characteristic flow velocity, $V_{thi}$![]() is ion thermal speed) and $\delta =\rho _i/L$
is ion thermal speed) and $\delta =\rho _i/L$![]() ($\rho _i$
($\rho _i$![]() is ion Larmor radius, $L$
is ion Larmor radius, $L$![]() is macroscopic scale length) (Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006).
is macroscopic scale length) (Schnack et al. Reference Schnack, Barnes, Brennan, Hegna, Held, Kim, Kruger, Pankin and Sovinec2006).
2.2. Linearisation of the extended MHD equations
In order to fulfil ${\boldsymbol {\nabla }} \boldsymbol {\cdot } {\boldsymbol B}=0$![]() , we use ${\boldsymbol B}= {\boldsymbol {\nabla }} \times {\boldsymbol A}$
, we use ${\boldsymbol B}= {\boldsymbol {\nabla }} \times {\boldsymbol A}$![]() ($\boldsymbol A$
($\boldsymbol A$![]() is magnetic vector potential), while the Weyl gauge (electric scalar potential $\varPhi _E =0$
is magnetic vector potential), while the Weyl gauge (electric scalar potential $\varPhi _E =0$![]() ) yields ${\boldsymbol E} = - ({\partial {\boldsymbol A}}/{\partial t})$
) yields ${\boldsymbol E} = - ({\partial {\boldsymbol A}}/{\partial t})$![]() . The time dependence of the perturbed quantities is assumed to be ${\sim }{\rm e}^{\lambda t}$
. The time dependence of the perturbed quantities is assumed to be ${\sim }{\rm e}^{\lambda t}$![]() with $\lambda =\gamma + {\rm i}\omega$
with $\lambda =\gamma + {\rm i}\omega$![]() ($\gamma$
($\gamma$![]() is growth rate, $\omega$
is growth rate, $\omega$![]() is oscillation frequency of the mode). Using the ansatz $f({\boldsymbol r},t)=f_0({\boldsymbol r})+ {\rm e}^{\lambda t}f_1({\boldsymbol r})$
is oscillation frequency of the mode). Using the ansatz $f({\boldsymbol r},t)=f_0({\boldsymbol r})+ {\rm e}^{\lambda t}f_1({\boldsymbol r})$![]() for $\rho,T,{\boldsymbol V}$
for $\rho,T,{\boldsymbol V}$![]() and ${\boldsymbol A}$
and ${\boldsymbol A}$![]() , the linearised forms of the extended fluid equations (2.1), (2.9), (2.3) and (2.14) read
, the linearised forms of the extended fluid equations (2.1), (2.9), (2.3) and (2.14) read


Here $\rho _0,{\boldsymbol V}_0, T_0$![]() and ${\boldsymbol A}_0$
and ${\boldsymbol A}_0$![]() are the equilibrium quantities of density, ion velocity (2.6), temperature ($T_0=T_{0e}+T_{0i}$
are the equilibrium quantities of density, ion velocity (2.6), temperature ($T_0=T_{0e}+T_{0i}$![]() ) and magnetic vector potential, while $\rho _1,{\boldsymbol V}_1, T_1$
) and magnetic vector potential, while $\rho _1,{\boldsymbol V}_1, T_1$![]() and ${\boldsymbol A}_1$
and ${\boldsymbol A}_1$![]() are their perturbations. The perturbation of the ion diamagnetic drift velocity reads
are their perturbations. The perturbation of the ion diamagnetic drift velocity reads

The corresponding boundary conditions and boundary terms of the linearised MHD equations are not affected by the newly implemented terms. They are described in detail in previous works (e.g. Huysmans et al. Reference Huysmans, Goedbloed and Kerner1993; Strumberger & Günter Reference Strumberger and Günter2017, Reference Strumberger and Günter2019).
3. Stability studies
The linearised, extended MHD equations (2.15)–(2.18) are implemented in the CASTOR3D code in general 3-D formulation. This general formulation allows one to use various flux coordinate types (Strumberger & Günter Reference Strumberger and Günter2017) (see also Appendix B). The parameter $\alpha ={m_i}/{e}$![]() is implemented in the form $\alpha =\alpha _s ({m_i}/{e})$
is implemented in the form $\alpha =\alpha _s ({m_i}/{e})$![]() , with $0\le \alpha _s \le 1$
, with $0\le \alpha _s \le 1$![]() being a scaling parameter. The latter allows the modification of the strength of the diamagnetic drift effects. This parameter is mainly necessary for computational reasons. Increasing $\alpha _s$
being a scaling parameter. The latter allows the modification of the strength of the diamagnetic drift effects. This parameter is mainly necessary for computational reasons. Increasing $\alpha _s$![]() step by step may lead from a growth rate without diamagnetic drift effects to a growth rate that is strongly reduced by these effects, or even to a stable solution. Certainly, only $\alpha _s=0$
step by step may lead from a growth rate without diamagnetic drift effects to a growth rate that is strongly reduced by these effects, or even to a stable solution. Certainly, only $\alpha _s=0$![]() and $\alpha _s=1$
and $\alpha _s=1$![]() yield physically relevant solutions.
yield physically relevant solutions.
Stability studies are performed for test equilibria assuming the following conditions: circular cross-section, minor radius $a=1$![]() m, aspect ratio $A=1.6$
m, aspect ratio $A=1.6$![]() , flat rotational transform profile (axis value $\iota _a=1.01$
, flat rotational transform profile (axis value $\iota _a=1.01$![]() , boundary value $\iota _b=0.63$
, boundary value $\iota _b=0.63$![]() ) and pressure profile defined by an analytical function $p(s)=p_a(1-2s^2+s^4)$
) and pressure profile defined by an analytical function $p(s)=p_a(1-2s^2+s^4)$![]() , with radial coordinate $s$
, with radial coordinate $s$![]() being the square root of the normalised toroidal flux. In figure 1(a) we show the rotational transform profile $\iota$
being the square root of the normalised toroidal flux. In figure 1(a) we show the rotational transform profile $\iota$![]() , the normalised pressure profile $p_N$
, the normalised pressure profile $p_N$![]() and the chosen normalised profiles of ion density $n_N$
and the chosen normalised profiles of ion density $n_N$![]() (deuterons) and temperature $T_N$
(deuterons) and temperature $T_N$![]() . We study the diamagnetic drift effects for an axisymmetric high-$\beta$
. We study the diamagnetic drift effects for an axisymmetric high-$\beta$![]() (volume-averaged plasma $\beta$
(volume-averaged plasma $\beta$![]() : $\langle \beta \rangle =2.97\,\%$
: $\langle \beta \rangle =2.97\,\%$![]() ) equilibrium and a low-$\beta$
) equilibrium and a low-$\beta$![]() ($\langle \beta \rangle =0.97\,\%$
($\langle \beta \rangle =0.97\,\%$![]() ) equilibrium, and a 3-D high-$\beta$
) equilibrium, and a 3-D high-$\beta$![]() ($\langle \beta \rangle =2.97\,\%$
($\langle \beta \rangle =2.97\,\%$![]() ) equilibrium with an $n=1$
) equilibrium with an $n=1$![]() helical core (see figure 1b). The latter is the result of a 3-D fixed-boundary equilibrium calculation with axisymmetric plasma boundary (Strumberger & Günter Reference Strumberger and Günter2017). All equilibria are computed with the 3-D NEMEC code (Hirshman & Whitson Reference Hirshman and Whitson1983; Hirshman, van Rij & Merkel Reference Hirshman, van Rij and Merkel1986). Ion and electron diamagnetic drift effects are investigated for various ratios of ion and electron pressures. We choose these simple test equilibria, because they are ideal and resistive unstable with respect to low- and medium-$n$
helical core (see figure 1b). The latter is the result of a 3-D fixed-boundary equilibrium calculation with axisymmetric plasma boundary (Strumberger & Günter Reference Strumberger and Günter2017). All equilibria are computed with the 3-D NEMEC code (Hirshman & Whitson Reference Hirshman and Whitson1983; Hirshman, van Rij & Merkel Reference Hirshman, van Rij and Merkel1986). Ion and electron diamagnetic drift effects are investigated for various ratios of ion and electron pressures. We choose these simple test equilibria, because they are ideal and resistive unstable with respect to low- and medium-$n$![]() internal modes, and they are numerically easy to handle. Due to their simple geometry and very flat $q$
internal modes, and they are numerically easy to handle. Due to their simple geometry and very flat $q$![]() -profile ($q=1/\iota$
-profile ($q=1/\iota$![]() ) only few poloidal and toroidal (3-D case) harmonics couple together. The resulting eigenvalue problems are, therefore, fast to solve, and allow detailed physical and numerical parameter studies.
) only few poloidal and toroidal (3-D case) harmonics couple together. The resulting eigenvalue problems are, therefore, fast to solve, and allow detailed physical and numerical parameter studies.

Figure 1. (a) Rotational transform profile $\iota$![]() and normalised profiles of pressure $p_N$
and normalised profiles of pressure $p_N$![]() , ion density $n_N$
, ion density $n_N$![]() and temperature $T_N$
and temperature $T_N$![]() as functions of the square root of the normalised toroidal flux $s$
as functions of the square root of the normalised toroidal flux $s$![]() . The dotted vertical line marks the position of the $\iota =1$
. The dotted vertical line marks the position of the $\iota =1$![]() rational flux surface. (b) Helical core of the 3-D equilibrium: $\iota =1$
rational flux surface. (b) Helical core of the 3-D equilibrium: $\iota =1$![]() flux surface and position of the magnetic axis (crosses) at the toroidal cross-sections $\varphi =0^{\circ }$
flux surface and position of the magnetic axis (crosses) at the toroidal cross-sections $\varphi =0^{\circ }$![]() , 90$^{\circ }$
, 90$^{\circ }$![]() , 180$^{\circ }$
, 180$^{\circ }$![]() and 270$^{\circ }$
and 270$^{\circ }$![]() .
.
3.1. Ideal stability studies (2-D equilibrium)
We study the stability of an axisymmetric high-$\beta$![]() equilibrium (pressure $p_a=33.75$
equilibrium (pressure $p_a=33.75$![]() kPa, deuteron ion density $n_a=0.7\times 10^{20}\,{\rm m}^{-3}$
kPa, deuteron ion density $n_a=0.7\times 10^{20}\,{\rm m}^{-3}$![]() and temperature $T_a=3009$
and temperature $T_a=3009$![]() eV at the magnetic axis) with equilibrium ion velocity ${\boldsymbol V_{i0}}=0$
eV at the magnetic axis) with equilibrium ion velocity ${\boldsymbol V_{i0}}=0$![]() , that is, we assume that the contributions to the ion velocity (2.6) are either zero or cancel. This equilibrium is unstable with respect to ideal modes localised at the $\iota =1$
, that is, we assume that the contributions to the ion velocity (2.6) are either zero or cancel. This equilibrium is unstable with respect to ideal modes localised at the $\iota =1$![]() rational flux surface. Using 2-D straight field line coordinates, the characteristic Fourier spectra of the real part of the radial velocity perturbation are shown for the $n=1$
rational flux surface. Using 2-D straight field line coordinates, the characteristic Fourier spectra of the real part of the radial velocity perturbation are shown for the $n=1$![]() and $n=10$
and $n=10$![]() modes in figures 2(a) and 2(b).
modes in figures 2(a) and 2(b).

Figure 2. Fourier spectra of the real part of the radial velocity perturbation for (a) an $n=1$![]() and (b) an $n=10$
and (b) an $n=10$![]() mode. The dotted vertical line indicates the position of the $\iota =1$
mode. The dotted vertical line indicates the position of the $\iota =1$![]() flux surface.
flux surface.
Recently, the diagnostic part of the CASTOR3D code has been extended by implementing the calculation of the resistive energy functional from the solution of the eigenvalue problem (Puchmayr et al. Reference Puchmayr, Dunne and Strumberger2022). This energy functional provides information on the different energetic drives of ideal and resistive modes. The energy of the perturbations is decomposed into stabilising contributions $\delta W_\text {STA}$![]() , the pressure-gradient drive $\delta W_\text {DP}$
, the pressure-gradient drive $\delta W_\text {DP}$![]() and the parallel current-density drive $\delta W_\text {CUR}$
and the parallel current-density drive $\delta W_\text {CUR}$![]() . For easy comparison of the energy across different perturbations, the energy values are normalised as described in Puchmayr et al. (Reference Puchmayr, Dunne and Strumberger2022), and we define the relative current-density drive as $\delta W_\text {CUR}/(\delta W_\text {CUR}+\delta W_\text {DP})$
. For easy comparison of the energy across different perturbations, the energy values are normalised as described in Puchmayr et al. (Reference Puchmayr, Dunne and Strumberger2022), and we define the relative current-density drive as $\delta W_\text {CUR}/(\delta W_\text {CUR}+\delta W_\text {DP})$![]() . The analysis of the ideal internal modes of the considered high-$\beta$
. The analysis of the ideal internal modes of the considered high-$\beta$![]() equilibrium shows that these modes are mainly pressure-gradient-driven. With increasing toroidal mode number, the perturbations get increasingly localised at the $q=1$
equilibrium shows that these modes are mainly pressure-gradient-driven. With increasing toroidal mode number, the perturbations get increasingly localised at the $q=1$![]() surface, where the equilibrium pressure gradient is high compared with that of the near-axis region, and become more pressure-gradient-driven. The $n=1$
surface, where the equilibrium pressure gradient is high compared with that of the near-axis region, and become more pressure-gradient-driven. The $n=1$![]() mode is the only mode that has a destabilising current density contribution at the magnetic axis, while the $n=2$
mode is the only mode that has a destabilising current density contribution at the magnetic axis, while the $n=2$![]() mode has a stabilising one (see figure 3b). There, the finite contributions result from the $m=1$
mode has a stabilising one (see figure 3b). There, the finite contributions result from the $m=1$![]() components of these two modes, while for the higher-$n$
components of these two modes, while for the higher-$n$![]() modes the $m=1$
modes the $m=1$![]() components are negligibly small at the magnetic axis. Furthermore, the integrated pressure-gradient drive $\delta W_\text {DP}$
components are negligibly small at the magnetic axis. Furthermore, the integrated pressure-gradient drive $\delta W_\text {DP}$![]() strongly increases with increasing toroidal mode number similarly to the resistive case shown in figure 7(c), while the integrated current-density drive $\delta W_\text {CUR}$
strongly increases with increasing toroidal mode number similarly to the resistive case shown in figure 7(c), while the integrated current-density drive $\delta W_\text {CUR}$![]() remains small due to the cancellation of stabilising and destabilising radial regions. So, these modes are most probably ideal internal kink and interchange modes.
remains small due to the cancellation of stabilising and destabilising radial regions. So, these modes are most probably ideal internal kink and interchange modes.

Figure 3. Energetic decomposition of the ideal internal perturbations of the considered high-$\beta$![]() equilibrium. (a) Relative current-density drive as a function of the toroidal mode number and (b) normalised energy density corresponding to the current-density drive as a function of the square root of the normalised toroidal flux.
equilibrium. (a) Relative current-density drive as a function of the toroidal mode number and (b) normalised energy density corresponding to the current-density drive as a function of the square root of the normalised toroidal flux.
We now investigate the effects of ion and electron magnetic drift on those ideal modes depending on the toroidal mode number $n$![]() . We determine the dominant effect by executing these computations for various ratios of the ion and electron pressures: (i) $p_i=p_e$
. We determine the dominant effect by executing these computations for various ratios of the ion and electron pressures: (i) $p_i=p_e$![]() , (ii) $p_i=\alpha _T p$
, (ii) $p_i=\alpha _T p$![]() , $p_e=(1-\alpha _T)p$
, $p_e=(1-\alpha _T)p$![]() with $\alpha _T=0.4$
with $\alpha _T=0.4$![]() and (iii) $p_i=0$
and (iii) $p_i=0$![]() , $p_e=p$
, $p_e=p$![]() (cold ions). A large stabilising effect is observed for $p_i=p_e$
(cold ions). A large stabilising effect is observed for $p_i=p_e$![]() and $p_i=0.4 p$
and $p_i=0.4 p$![]() . The growth rates are reducedand the modes oscillate with negative frequencies. The modes are stabilised when the absolute value of the oscillation frequency $|\omega |$
. The growth rates are reducedand the modes oscillate with negative frequencies. The modes are stabilised when the absolute value of the oscillation frequency $|\omega |$![]() of the mode exceeds the ideal growth rate, $|\omega | \gtrapprox \gamma _{{\rm ideal}}$
of the mode exceeds the ideal growth rate, $|\omega | \gtrapprox \gamma _{{\rm ideal}}$![]() . Therefore, the considered modes are stable for $p_i=0.5 p, n > 6$
. Therefore, the considered modes are stable for $p_i=0.5 p, n > 6$![]() and $p_i=0.4 p, n > 8$
and $p_i=0.4 p, n > 8$![]() , as shown in figures 4(a) and 4(b) and verified in figures 4(c) and 4(d). Growth rates and oscillation frequencies are plotted as functions of the scaling parameter $\alpha _s$
, as shown in figures 4(a) and 4(b) and verified in figures 4(c) and 4(d). Growth rates and oscillation frequencies are plotted as functions of the scaling parameter $\alpha _s$![]() in the latter two figures. There, the $n=7$
in the latter two figures. There, the $n=7$![]() and $n=9$
and $n=9$![]() modes stabilise for $p_i=0.5p$
modes stabilise for $p_i=0.5p$![]() , $\alpha _s\ge 0.9705$
, $\alpha _s\ge 0.9705$![]() and $p_i=0.4p$
and $p_i=0.4p$![]() , $\alpha _s\ge 0.9574$
, $\alpha _s\ge 0.9574$![]() , respectively. The oscillation frequencies scale in good agreement with the toroidal mode number $n$
, respectively. The oscillation frequencies scale in good agreement with the toroidal mode number $n$![]() (figure 4a,b) and the scaling parameter $\alpha _s$
(figure 4a,b) and the scaling parameter $\alpha _s$![]() (figure 4c,d). A small deviation from the linear increase of $\omega$
(figure 4c,d). A small deviation from the linear increase of $\omega$![]() as function of $\alpha _s$
as function of $\alpha _s$![]() only appears close to stabilising $\alpha _s$
only appears close to stabilising $\alpha _s$![]() value when $|\omega |$
value when $|\omega |$![]() exceeds $\gamma _{{\rm ideal}}$
exceeds $\gamma _{{\rm ideal}}$![]() . Although the two considered pressure ratios do not differ much, there are significant differences in growth rates, oscillation frequencies and the lowest $n$
. Although the two considered pressure ratios do not differ much, there are significant differences in growth rates, oscillation frequencies and the lowest $n$![]() values of the stable modes.
values of the stable modes.

Figure 4. Assuming (a,c) $p_i=p_e=0.5 p$![]() and (b,d) $p_i=0.4 p$
and (b,d) $p_i=0.4 p$![]() , $p_e=0.6 p$
, $p_e=0.6 p$![]() , growth rate $\gamma$
, growth rate $\gamma$![]() and absolute value of the oscillation frequency $|\omega |$
and absolute value of the oscillation frequency $|\omega |$![]() are plotted (a,b) as functions of the toroidal mode number $n$
are plotted (a,b) as functions of the toroidal mode number $n$![]() and (c,d) as functions of the scaling parameter $\alpha _s$
and (c,d) as functions of the scaling parameter $\alpha _s$![]() for (c) the $n$
for (c) the $n$![]() =7 and (d) the $n$
=7 and (d) the $n$![]() =9 modes. (a,b) The blue stars represent the absolute value of half of the ion diamagnetic drift frequency ${|\omega _i^*|}/{2}$
=9 modes. (a,b) The blue stars represent the absolute value of half of the ion diamagnetic drift frequency ${|\omega _i^*|}/{2}$![]() (A2). The black dashed lines mark the growth rates $\gamma _{{\rm ideal}}$
(A2). The black dashed lines mark the growth rates $\gamma _{{\rm ideal}}$![]() obtained without taking diamagnetic drift effects into account.
obtained without taking diamagnetic drift effects into account.
The obtained results are in good agreement with the results and the dispersion relation

presented in Aiba (Reference Aiba2016), that is, the modes are marginally stable for $\gamma _{{\rm ideal}}= \omega _i^*/2$![]() . A simplified analytical expression of $\omega _i^*$
. A simplified analytical expression of $\omega _i^*$![]() is presented in Appendix A. The resulting ion drift frequencies are $|\omega _i^*|=5841$
is presented in Appendix A. The resulting ion drift frequencies are $|\omega _i^*|=5841$![]() rad s$^{-1}$
rad s$^{-1}$![]() ($p_i=0.5p$
($p_i=0.5p$![]() ) and 4673 rad s$^{-1}$
) and 4673 rad s$^{-1}$![]() ($p_i=0.4p$
($p_i=0.4p$![]() ) for a 1/1 mode at the $\iota =1$
) for a 1/1 mode at the $\iota =1$![]() flux surface. The calculated drift frequencies $|\omega _i^*|/2$
flux surface. The calculated drift frequencies $|\omega _i^*|/2$![]() are compared with the oscillation frequencies of the modes in figures 4(a) and 4(b). They agree very well as stated by (3.1). Comparing the numerical results shown in figures 4(c) and 4(d) with the calculated drift frequencies, we obtain $\gamma _{{\rm ideal}}(n=7) = 19\,556\,{\rm rad}\,{\rm s}^{-1} \approx |\omega |= 19\,805\,{\rm rad}\,{\rm s}^{-1}\approx \alpha _s |\omega _i^*|/2 = 19\,840\,{\rm rad}\,{\rm s}^{-1}$
are compared with the oscillation frequencies of the modes in figures 4(a) and 4(b). They agree very well as stated by (3.1). Comparing the numerical results shown in figures 4(c) and 4(d) with the calculated drift frequencies, we obtain $\gamma _{{\rm ideal}}(n=7) = 19\,556\,{\rm rad}\,{\rm s}^{-1} \approx |\omega |= 19\,805\,{\rm rad}\,{\rm s}^{-1}\approx \alpha _s |\omega _i^*|/2 = 19\,840\,{\rm rad}\,{\rm s}^{-1}$![]() and $\gamma _{{\rm ideal}}(n=9) = 19\,804\,{\rm rad}\,{\rm s}^{-1} \approx |\omega |= 20\,082\,{\rm rad}\,{\rm s}^{-1}\approx \alpha _s |\omega _i^*|/2 = 20\,132\,{\rm rad}\,{\rm s}^{-1}$
and $\gamma _{{\rm ideal}}(n=9) = 19\,804\,{\rm rad}\,{\rm s}^{-1} \approx |\omega |= 20\,082\,{\rm rad}\,{\rm s}^{-1}\approx \alpha _s |\omega _i^*|/2 = 20\,132\,{\rm rad}\,{\rm s}^{-1}$![]() , respectively. Here the used expression (A2) is a good approximation for $\omega _i^*$
, respectively. Here the used expression (A2) is a good approximation for $\omega _i^*$![]() , because the Fourier spectra of the considered modes are dominated by only one poloidal harmonic (see figure 2). Besides, the ion diamagnetic drift is the dominant effect for these ideal modes, while the electron diamagnetic drift effect is negligible, as shown in figure 5. There, growth rate and oscillation frequency (marked by red crosses) are presented as functions of the toroidal mode number $n$
, because the Fourier spectra of the considered modes are dominated by only one poloidal harmonic (see figure 2). Besides, the ion diamagnetic drift is the dominant effect for these ideal modes, while the electron diamagnetic drift effect is negligible, as shown in figure 5. There, growth rate and oscillation frequency (marked by red crosses) are presented as functions of the toroidal mode number $n$![]() for a plasma with cold ions ($p_i=0$
for a plasma with cold ions ($p_i=0$![]() ). That is, there is no ion, but only an electron diamagnetic drift represented by the parallel electron pressure-gradient term in (2.11) (Yu, Günter & Scott Reference Yu, Günter and Scott2003). Here, however, the latter has no stabilising effect, but an insignificant destabilising effect. It causes mode oscillations with frequencies increasing linearly with $n$
). That is, there is no ion, but only an electron diamagnetic drift represented by the parallel electron pressure-gradient term in (2.11) (Yu, Günter & Scott Reference Yu, Günter and Scott2003). Here, however, the latter has no stabilising effect, but an insignificant destabilising effect. It causes mode oscillations with frequencies increasing linearly with $n$![]() , but which are negligibly small in comparison with the mode frequencies induced by the ion diamagnetic drift effect.
, but which are negligibly small in comparison with the mode frequencies induced by the ion diamagnetic drift effect.

Figure 5. (a) Growth rate and (b) absolute value of the oscillation frequency ($\omega < 0$![]() ) as functions of the toroidal mode number $n$
) as functions of the toroidal mode number $n$![]() assuming cold ions ($\alpha _T=0)$
assuming cold ions ($\alpha _T=0)$![]() (red crosses). In (a) the black solid line marks the growth rate $\gamma _{{\rm ideal}}$
(red crosses). In (a) the black solid line marks the growth rate $\gamma _{{\rm ideal}}$![]() obtained without taking diamagnetic drift effects into account.
obtained without taking diamagnetic drift effects into account.
3.2. Resistive stability studies (2-D equilibrium)
We consider the same plasma configuration as for the ideal modes, but with a much lower plasma $\beta$![]() of $\langle \beta \rangle =0.97\,\%$
of $\langle \beta \rangle =0.97\,\%$![]() (pressure $p_a=11.25$
(pressure $p_a=11.25$![]() kPa, deuteron ion density $n_a=0.7\times 10^{20}\,{\rm m}^{-3}$
kPa, deuteron ion density $n_a=0.7\times 10^{20}\,{\rm m}^{-3}$![]() and temperature $T_a=1004$
and temperature $T_a=1004$![]() eV at the magnetic axis). Again, we assume that all contributions to the equilibrium ion velocity are either zero or cancel ($\boldsymbol {V}_{i0}=0$
eV at the magnetic axis). Again, we assume that all contributions to the equilibrium ion velocity are either zero or cancel ($\boldsymbol {V}_{i0}=0$![]() ). This low-$\beta$
). This low-$\beta$![]() equilibrium is also unstable with respect to internal modes located at the $\iota =1$
equilibrium is also unstable with respect to internal modes located at the $\iota =1$![]() flux surface. These modes show an analogous mode structure as the ideal modes considered in the previous section (compare figures 2a,b and 6c,d). However, they are only unstable for finite plasma resistivity $\eta$
flux surface. These modes show an analogous mode structure as the ideal modes considered in the previous section (compare figures 2a,b and 6c,d). However, they are only unstable for finite plasma resistivity $\eta$![]() , and their slow growth rates approximately scale with $\eta ^{1/3}$
, and their slow growth rates approximately scale with $\eta ^{1/3}$![]() as shown in figure 6(b) (we assume $\eta = {\rm constant}$
as shown in figure 6(b) (we assume $\eta = {\rm constant}$![]() ). This scaling is typical for resistive kink and interchange modes.
). This scaling is typical for resistive kink and interchange modes.

Figure 6. (a) Growth rates as functions of the toroidal mode number $n$![]() for $\eta =10^{-6}$
for $\eta =10^{-6}$![]() and $\eta =10^{-7}\,\Omega \,{\rm m}$
and $\eta =10^{-7}\,\Omega \,{\rm m}$![]() . (b) Growth rates as functions of $\eta$
. (b) Growth rates as functions of $\eta$![]() for $n=1$
for $n=1$![]() , 4 and 20. The red dashed line indicates the $\eta ^{1/3}$
, 4 and 20. The red dashed line indicates the $\eta ^{1/3}$![]() scaling. Fourier spectra of the real part of the radial velocity perturbation are shown for (c) an $n=1$
scaling. Fourier spectra of the real part of the radial velocity perturbation are shown for (c) an $n=1$![]() and (d) an $n=10$
and (d) an $n=10$![]() mode. The blue dotted vertical lines indicate the position of the $\iota =1$
mode. The blue dotted vertical lines indicate the position of the $\iota =1$![]() rational flux surface.
rational flux surface.
Analysing the resistive energy functional of these modes highlights their pressure-gradient-driven character. Compared with the ideal modes of the high-$\beta$![]() equilibrium, the resistive modes of the low-$\beta$
equilibrium, the resistive modes of the low-$\beta$![]() equilibrium are overall more pressure- gradient-driven (compare figures 3a and 7a). Similarly to the ideal modes, the relative current-density drive strongly decreases with increasing toroidal mode number. Although the relative current-density drive is nearly independent of the resistivity, one can see that the perturbation and the corresponding energy densities are broadened with increasing resistivity (see figure 7b,d). We remark that the precise calculation of the energetic decomposition for the $n=1$
equilibrium are overall more pressure- gradient-driven (compare figures 3a and 7a). Similarly to the ideal modes, the relative current-density drive strongly decreases with increasing toroidal mode number. Although the relative current-density drive is nearly independent of the resistivity, one can see that the perturbation and the corresponding energy densities are broadened with increasing resistivity (see figure 7b,d). We remark that the precise calculation of the energetic decomposition for the $n=1$![]() mode is numerically challenging as the perturbation is finite at the magnetic axis, where the coordinate system is singular. For larger toroidal mode numbers, the resistive modes become increasingly localised at the $\iota =1$
mode is numerically challenging as the perturbation is finite at the magnetic axis, where the coordinate system is singular. For larger toroidal mode numbers, the resistive modes become increasingly localised at the $\iota =1$![]() flux surface (see figure 7d). The pressure-gradient drive $\delta W_\text {DP}$
flux surface (see figure 7d). The pressure-gradient drive $\delta W_\text {DP}$![]() strongly increases with increasing toroidal mode number, whereas the integrated current-density drive $\delta W_\text {CUR}$
strongly increases with increasing toroidal mode number, whereas the integrated current-density drive $\delta W_\text {CUR}$![]() remains small because of the cancellation of stabilising and destabilising contributions in different radial regions of the plasma (see figure 7c,d).
remains small because of the cancellation of stabilising and destabilising contributions in different radial regions of the plasma (see figure 7c,d).

Figure 7. Energetic decomposition of the resistive internal perturbations of the considered low-beta equilibrium: (a) Relative current-density drive as a function of the toroidal mode number for resistivities of $\eta =10^{-7}\,\Omega \,{\rm m}$![]() (blue) and $\eta =10^{-6}\,\Omega \,{\rm m}$
(blue) and $\eta =10^{-6}\,\Omega \,{\rm m}$![]() (orange). Normalised energy densities corresponding to (b,d) the current-density and (c) the pressure-gradient drives as a function of the square root of the normalised toroidal flux for resistivities of (b) $\eta =10^{-7}\,\Omega \,{\rm m}$
(orange). Normalised energy densities corresponding to (b,d) the current-density and (c) the pressure-gradient drives as a function of the square root of the normalised toroidal flux for resistivities of (b) $\eta =10^{-7}\,\Omega \,{\rm m}$![]() and (c,d) $\eta =10^{-6}\,\Omega \,{\rm m}$
and (c,d) $\eta =10^{-6}\,\Omega \,{\rm m}$![]() .
.
Figures 8 and 9 show growth rates and oscillation frequencies as functions of the parameter $\alpha _T$![]() and the toroidal mode number $n$
and the toroidal mode number $n$![]() , respectively. They include the limiting cases of cold ions ($\alpha _T=0$
, respectively. They include the limiting cases of cold ions ($\alpha _T=0$![]() ) and cold electrons ($\alpha _T=1$
) and cold electrons ($\alpha _T=1$![]() ). In the case of cold ions, only the electron diamagnetic drift remains that is described by the parallel electron pressure-gradient term in the extended Ohm's law (2.11). In the case of cold electrons, only the ion diamagnetic drift influences the stability via the gyro-viscosity term in the momentum equation (2.9) and the perpendicular ion pressure-gradient term in (2.11). The comparison of the growth rates without (figure 6a) and with (figure 8a,c) diamagnetic drift effects shows a large stabilising effect for all combinations of ion and electron pressures. However, resistivity and electron temperature are coupled by the Spitzer resistivity in a real plasma. Using a rough estimate of the Spitzer resistivity, namely $\eta =2.8\times 10^{-8}/ T_e^{3/2}\,\Omega \,{\rm m}$
). In the case of cold ions, only the electron diamagnetic drift remains that is described by the parallel electron pressure-gradient term in the extended Ohm's law (2.11). In the case of cold electrons, only the ion diamagnetic drift influences the stability via the gyro-viscosity term in the momentum equation (2.9) and the perpendicular ion pressure-gradient term in (2.11). The comparison of the growth rates without (figure 6a) and with (figure 8a,c) diamagnetic drift effects shows a large stabilising effect for all combinations of ion and electron pressures. However, resistivity and electron temperature are coupled by the Spitzer resistivity in a real plasma. Using a rough estimate of the Spitzer resistivity, namely $\eta =2.8\times 10^{-8}/ T_e^{3/2}\,\Omega \,{\rm m}$![]() ($T_e$
($T_e$![]() in keV, Coulomb logarithm $\ln \varLambda =17$
in keV, Coulomb logarithm $\ln \varLambda =17$![]() ) (Wesson Reference Wesson1997), we obtain $T_e=0.09$
) (Wesson Reference Wesson1997), we obtain $T_e=0.09$![]() and $T_e=0.43$
and $T_e=0.43$![]() keV for $\eta =10^{-6}$
keV for $\eta =10^{-6}$![]() and $\eta =10^{-7}\,\Omega$
and $\eta =10^{-7}\,\Omega$![]() m, respectively. The corresponding $\alpha _T$
m, respectively. The corresponding $\alpha _T$![]() parameters are marked by the dotted vertical lines in figure 8. Cold ions ($\alpha _T=0$
parameters are marked by the dotted vertical lines in figure 8. Cold ions ($\alpha _T=0$![]() ) would correspond to an electron temperature of $T_e=1$
) would correspond to an electron temperature of $T_e=1$![]() keV and a small resistivity of $\eta =2.8\times 10^{-8}\,\Omega$
keV and a small resistivity of $\eta =2.8\times 10^{-8}\,\Omega$![]() m. Extrapolating the results presented in figures 8(a,c) and 9(a,c), we expect that, at least, all modes with $n>1$
m. Extrapolating the results presented in figures 8(a,c) and 9(a,c), we expect that, at least, all modes with $n>1$![]() are stabilised by the electron diamagnetic drift effect. However, CASTOR3D computations show that also the $n=1$
are stabilised by the electron diamagnetic drift effect. However, CASTOR3D computations show that also the $n=1$![]() mode is stabilised for $\eta =2.8\times 10^{-8}\,\Omega$
mode is stabilised for $\eta =2.8\times 10^{-8}\,\Omega$![]() m and $\alpha _T=0$
m and $\alpha _T=0$![]() .
.

Figure 8. (a,c) Growth rates and (b,d) oscillation frequencies as functions of parameter $\alpha _T$![]() for various $n$
for various $n$![]() . The dotted vertical lines mark the $\alpha _T$
. The dotted vertical lines mark the $\alpha _T$![]() values for which the considered resistivity value corresponds to the approximated Spitzer resistivity. The stars denote $\omega _i^*$
values for which the considered resistivity value corresponds to the approximated Spitzer resistivity. The stars denote $\omega _i^*$![]() .
.

Figure 9. (a,c) Growth rates and (b,d) oscillation frequencies as functions of the toroidal mode number $n$![]() for various $\alpha _T$
for various $\alpha _T$![]() values: $\alpha _T=0$
values: $\alpha _T=0$![]() (red solid line with squares), $\alpha _T=0.05$
(red solid line with squares), $\alpha _T=0.05$![]() (blue solid line with circles), $\alpha _T=0.1$
(blue solid line with circles), $\alpha _T=0.1$![]() (magenta solid line with plus symbols), $\alpha _T=0.5$
(magenta solid line with plus symbols), $\alpha _T=0.5$![]() (green solid line) and $\alpha _T=1$
(green solid line) and $\alpha _T=1$![]() (resistive modes without zero crossing: black crosses; resistive modes with one zero crossing: black diamonds). The orange circle marks the change of the mode type.
(resistive modes without zero crossing: black crosses; resistive modes with one zero crossing: black diamonds). The orange circle marks the change of the mode type.
The oscillation frequencies of the modes scale linearly with $\alpha _T$![]() (figure 8b,d) and $n$
(figure 8b,d) and $n$![]() (figure 9b,d), at least for $\alpha _T > 0.2$
(figure 9b,d), at least for $\alpha _T > 0.2$![]() . The deviation from the linear scaling is negligibly small and, therefore, would only be visible in an enlargement of the figures. The stars mark the ion diamagnetic drift frequencies for the corresponding toroidal mode numbers. These frequencies agree very well with the oscillation frequencies of the modes, that is, $\omega \approx \omega _i^*$
. The deviation from the linear scaling is negligibly small and, therefore, would only be visible in an enlargement of the figures. The stars mark the ion diamagnetic drift frequencies for the corresponding toroidal mode numbers. These frequencies agree very well with the oscillation frequencies of the modes, that is, $\omega \approx \omega _i^*$![]() , while $\omega \approx \omega _i^*/2$
, while $\omega \approx \omega _i^*/2$![]() holds for the ideal modes (see § 3.1). Diamagnetic drift effects not only cause modes to oscillate in time, reduce growth rates or even stabilise modes, but may also make a less unstable mode to the most unstable one. The considered low-$\beta$
holds for the ideal modes (see § 3.1). Diamagnetic drift effects not only cause modes to oscillate in time, reduce growth rates or even stabilise modes, but may also make a less unstable mode to the most unstable one. The considered low-$\beta$![]() equilibrium is unstable with respect to resistive kink and interchange modes (figures 8c,d and 10a,c), whose radial velocity perturbation (which is equivalent to the radial displacement) does not change its sign (no zero crossing). However, the equilibrium is also unstable to resistive modes whose radial velocity perturbation changes once its sign changes (one zero crossing) (figure 10b,d). The resistive energy functionals of the latter show a pressure-gradient drive of almost 100 %, that is, the considered equilibrium is unstable with respect to a so-called Sturmian sequence of modes (Goedbloed & Sakanaka Reference Goedbloed and Sakanaka1974). The considered modes with one zero crossing are mostly less unstable than the modes without zero crossing. However, in the case of cold electrons the resistive $n=2$
equilibrium is unstable with respect to resistive kink and interchange modes (figures 8c,d and 10a,c), whose radial velocity perturbation (which is equivalent to the radial displacement) does not change its sign (no zero crossing). However, the equilibrium is also unstable to resistive modes whose radial velocity perturbation changes once its sign changes (one zero crossing) (figure 10b,d). The resistive energy functionals of the latter show a pressure-gradient drive of almost 100 %, that is, the considered equilibrium is unstable with respect to a so-called Sturmian sequence of modes (Goedbloed & Sakanaka Reference Goedbloed and Sakanaka1974). The considered modes with one zero crossing are mostly less unstable than the modes without zero crossing. However, in the case of cold electrons the resistive $n=2$![]() mode with one zero crossing remains unstable, while the corresponding mode without zero crossing is stabilised by the ion diamagnetic drift effect as shown in figure 9(a,c). There, the growth rates of both mode types are presented for $\alpha _T=1$
mode with one zero crossing remains unstable, while the corresponding mode without zero crossing is stabilised by the ion diamagnetic drift effect as shown in figure 9(a,c). There, the growth rates of both mode types are presented for $\alpha _T=1$![]() . In figure 10 the Fourier spectra of the real part of the radial velocity perturbation are presented for both $n=3$
. In figure 10 the Fourier spectra of the real part of the radial velocity perturbation are presented for both $n=3$![]() mode types without and with diamagnetic drift effects taken into account. Since the $n=2$
mode types without and with diamagnetic drift effects taken into account. Since the $n=2$![]() mode without zero crossing is stable for $\alpha _T=1$
mode without zero crossing is stable for $\alpha _T=1$![]() , the Fourier spectra are presented for the $n=3$
, the Fourier spectra are presented for the $n=3$![]() modes which have analogous structures.
modes which have analogous structures.

Figure 10. Fourier spectra of the real part of the radial velocity perturbations for (a,c) the resistive $n=3$![]() mode without zero crossing and (b,d) the resistive $n=3$
mode without zero crossing and (b,d) the resistive $n=3$![]() mode with one zero crossing (a,b) without and (c,d) with taking ion diamagnetic drift effects into account.
mode with one zero crossing (a,b) without and (c,d) with taking ion diamagnetic drift effects into account.
3.3. Ideal stability studies (3-D equilibrium)
The 3-D, stellarator-symmetric, high-$\beta$![]() equilibrium differs from the previous considered up–down symmetric, axisymmetric equilibrium by an $n=1$
equilibrium differs from the previous considered up–down symmetric, axisymmetric equilibrium by an $n=1$![]() helical core. Analogous to the axisymmetric one, this 3-D equilibrium is unstable with respect to ideal kink and interchange modes. Again, the ion diamagnetic drift effect taken into account by the gyro-viscosity term in the momentum equation (2.9) is the dominant effect, while the contributions of the pressure terms in Ohm's law (2.14) are negligibly small (see also Appendix B). However, particularly in 3-D geometry these drift terms cause additional numerical problems. That is, they increase the occurrence of non-physical ‘parasitic’ solutions, and lead to non-physical oscillations of the eigenfunctions. We therefore have neglected these terms in the following computations. Certainly, the pressure terms can only be neglected in Ohm's law in the case of highly unstable ideal modes (see § 3.1), but they play an essential role in the case of resistive modes as shown in § 3.2. The eigenvalue problem in general 3-D formulation yields two orthogonal solutions for an instability. The corresponding growth rates (real parts of the eigenvalues) are always equal (degenerate) for axisymmetric configurations, but they may be different (non-degenerate) in the case of 3-D configurations. Finite oscillation frequencies (imaginary parts of the eigenvalues) always have the same absolute values, but opposite signs ($\omega _1=-\omega _2$
helical core. Analogous to the axisymmetric one, this 3-D equilibrium is unstable with respect to ideal kink and interchange modes. Again, the ion diamagnetic drift effect taken into account by the gyro-viscosity term in the momentum equation (2.9) is the dominant effect, while the contributions of the pressure terms in Ohm's law (2.14) are negligibly small (see also Appendix B). However, particularly in 3-D geometry these drift terms cause additional numerical problems. That is, they increase the occurrence of non-physical ‘parasitic’ solutions, and lead to non-physical oscillations of the eigenfunctions. We therefore have neglected these terms in the following computations. Certainly, the pressure terms can only be neglected in Ohm's law in the case of highly unstable ideal modes (see § 3.1), but they play an essential role in the case of resistive modes as shown in § 3.2. The eigenvalue problem in general 3-D formulation yields two orthogonal solutions for an instability. The corresponding growth rates (real parts of the eigenvalues) are always equal (degenerate) for axisymmetric configurations, but they may be different (non-degenerate) in the case of 3-D configurations. Finite oscillation frequencies (imaginary parts of the eigenvalues) always have the same absolute values, but opposite signs ($\omega _1=-\omega _2$![]() ). However, those opposite signs do not mean that the corresponding modes rotate or oscillate contrarily. In fact, they rotate in the same direction as an illustration of the rotation in real space would show. In figure 11 the two growth rates of the instabilities are marked by dots and diamonds for the considered 3-D equilibrium. Here only the growth rates of the $n^*=1$
). However, those opposite signs do not mean that the corresponding modes rotate or oscillate contrarily. In fact, they rotate in the same direction as an illustration of the rotation in real space would show. In figure 11 the two growth rates of the instabilities are marked by dots and diamonds for the considered 3-D equilibrium. Here only the growth rates of the $n^*=1$![]() internal kink mode without diamagnetic drift effects are slightly non-degenerate. We characterise the modes as $n^*$
internal kink mode without diamagnetic drift effects are slightly non-degenerate. We characterise the modes as $n^*$![]() , because in 3-D geometry several $n$
, because in 3-D geometry several $n$![]() harmonics couple together and contribute to the Fourier spectrum of a mode, that is, $n^*$
harmonics couple together and contribute to the Fourier spectrum of a mode, that is, $n^*$![]() indicates the toroidal mode number of the global mode structure. As already mentioned in the introduction, in many cases $n^*$
indicates the toroidal mode number of the global mode structure. As already mentioned in the introduction, in many cases $n^*$![]() corresponds to the dominant toroidal Fourier harmonic contributing to the mode. In figure 13(a,b) the structures of the two solutions obtained without diamagnetic drift effects are shown for an $n^*=1$
corresponds to the dominant toroidal Fourier harmonic contributing to the mode. In figure 13(a,b) the structures of the two solutions obtained without diamagnetic drift effects are shown for an $n^*=1$![]() mode. They are orthogonal to each other, and they correspond to pure cosine (figure 13a) and sine (figure 13b) functions, because of the stellarator-symmetric equilibrium. In the case of an axisymmetric configuration the two structures would be equivalent, that is, one structure could be transformed into the other by multiplying the eigenfunctions with ${\rm e}^{{\rm i}\phi }$
mode. They are orthogonal to each other, and they correspond to pure cosine (figure 13a) and sine (figure 13b) functions, because of the stellarator-symmetric equilibrium. In the case of an axisymmetric configuration the two structures would be equivalent, that is, one structure could be transformed into the other by multiplying the eigenfunctions with ${\rm e}^{{\rm i}\phi }$![]() (toroidal angle $\phi =\pm 90^{\circ }$
(toroidal angle $\phi =\pm 90^{\circ }$![]() ). Such a transformation is not possible in 3-D geometry. While, for the given example, the radial velocity perturbation (which in linear MHD is equivalent to the displacement of the mode) is perpendicular to the displacement of the helical core in figure 13(a), it is parallel in figure 13(b). These different locations result in the slightly unequal growth rates given in 13(a,b). (This small difference of the growth rates would only be well visible in an enlargement of figure 11.) The perturbation perpendicular to the helical core grows faster than the perturbation parallel to it. For a more detailed discussion of fast- and slow-growing solutions in 3-D tokamak configurations we refer the reader to Puchmayr et al. (Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). For completeness, it should also be mentioned that the complex linear eigenvalue problem, which is solved by the CASTOR3D code, can be multiplied with any complex number ($\ne 0$
). Such a transformation is not possible in 3-D geometry. While, for the given example, the radial velocity perturbation (which in linear MHD is equivalent to the displacement of the mode) is perpendicular to the displacement of the helical core in figure 13(a), it is parallel in figure 13(b). These different locations result in the slightly unequal growth rates given in 13(a,b). (This small difference of the growth rates would only be well visible in an enlargement of figure 11.) The perturbation perpendicular to the helical core grows faster than the perturbation parallel to it. For a more detailed discussion of fast- and slow-growing solutions in 3-D tokamak configurations we refer the reader to Puchmayr et al. (Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). For completeness, it should also be mentioned that the complex linear eigenvalue problem, which is solved by the CASTOR3D code, can be multiplied with any complex number ($\ne 0$![]() ). That is, amplitudes and signs of the eigenfunctions are not determined.
). That is, amplitudes and signs of the eigenfunctions are not determined.

Figure 11. Growth rates $\gamma$![]() and absolute values of the oscillation frequency $|\omega |$
and absolute values of the oscillation frequency $|\omega |$![]() as functions of $n^*$
as functions of $n^*$![]() for the axisymmetric equilibrium (solid lines) and the 3-D equilibrium (dots and diamonds) with (red) and without (black) taking diamagnetic drift effects into account. The blue stars represent the absolute value of half of the ion diamagnetic drift frequency $|\omega _i^*|/2$
for the axisymmetric equilibrium (solid lines) and the 3-D equilibrium (dots and diamonds) with (red) and without (black) taking diamagnetic drift effects into account. The blue stars represent the absolute value of half of the ion diamagnetic drift frequency $|\omega _i^*|/2$![]() .
.
In figure 11 the eigenvalues of the low-$n^*$![]() modes are shown as a function of $n^*$
modes are shown as a function of $n^*$![]() with and without taking the ion diamagnetic drift effect into account, and assuming $\alpha _T=0.5$
with and without taking the ion diamagnetic drift effect into account, and assuming $\alpha _T=0.5$![]() . While without diamagnetic drift effects the $n^*=1$
. While without diamagnetic drift effects the $n^*=1$![]() growth rates are appreciably non-degenerate (see also figure 12a), they become degenerate when taking those effects into account. As expected, the induced oscillation frequencies have opposite signs and equal absolute values. The latter agree to a good approximation with the high-$\beta$
growth rates are appreciably non-degenerate (see also figure 12a), they become degenerate when taking those effects into account. As expected, the induced oscillation frequencies have opposite signs and equal absolute values. The latter agree to a good approximation with the high-$\beta$![]() axisymmetric results and half the value of the ion diamagnetic drift frequency, $|\omega _i^*|/2$
axisymmetric results and half the value of the ion diamagnetic drift frequency, $|\omega _i^*|/2$![]() . Although the eigenvalues of the modes are very similar for the 3-D and the axisymmetric equilibria, there are two noteworthy differences between the two cases which we discuss in the following.
. Although the eigenvalues of the modes are very similar for the 3-D and the axisymmetric equilibria, there are two noteworthy differences between the two cases which we discuss in the following.

Figure 12. (a) Growth rates and (b) oscillation frequencies of the two possible $n^*=1$![]() modes as functions of the scaling parameter $\alpha _s$
modes as functions of the scaling parameter $\alpha _s$![]() (enlargement of the interesting region). The green dotted lines ($\alpha _s=0.01875$
(enlargement of the interesting region). The green dotted lines ($\alpha _s=0.01875$![]() ) mark the limit when the growth rates become degenerate and the modes start to oscillate.
) mark the limit when the growth rates become degenerate and the modes start to oscillate.
(a) If the growth rates of the two orthogonal solutions are different (non-degenerate) in the case without diamagnetic drift, a minimum strength of the diamagnetic drift effect (which corresponds to a minimum drift frequency) is necessary to equalise the growth rates and to start the mode oscillation. In figure 12 the growth rates and oscillation frequencies of the two possible $n^*=1$![]() modes are shown as functions of the scaling parameter $\alpha _s$
modes are shown as functions of the scaling parameter $\alpha _s$![]() . The initially non-degenerate growth rates converge until they become equal, while the modes start to oscillate ($\omega _1=-\omega _2$
. The initially non-degenerate growth rates converge until they become equal, while the modes start to oscillate ($\omega _1=-\omega _2$![]() ). The opposite signs of the oscillation frequencies result in the same oscillation cycle, but are phase-shifted in time. An analogous behaviour has been observed with respect to plasma rotation in the case of external kink modes of a quasi-axisymmetric stellarator equilibrium (Strumberger & Günter Reference Strumberger and Günter2019) and edge-localised modes in 3-D tokamak equilibria (Puchmayr et al. Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). There, a minimum plasma rotation frequency is required for modes with non-degenerate growth rates to start oscillation. In figure 13 the vectors characterise the radial velocity perturbation in the $R$
). The opposite signs of the oscillation frequencies result in the same oscillation cycle, but are phase-shifted in time. An analogous behaviour has been observed with respect to plasma rotation in the case of external kink modes of a quasi-axisymmetric stellarator equilibrium (Strumberger & Günter Reference Strumberger and Günter2019) and edge-localised modes in 3-D tokamak equilibria (Puchmayr et al. Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). There, a minimum plasma rotation frequency is required for modes with non-degenerate growth rates to start oscillation. In figure 13 the vectors characterise the radial velocity perturbation in the $R$![]() –$Z$
–$Z$![]() plane at toroidal angle $\varphi =0^{\circ }$
plane at toroidal angle $\varphi =0^{\circ }$![]() and time $t=0$
and time $t=0$![]() ($t=0$
($t=0$![]() refers to the mode structure at the beginning of an oscillation cycle). Taking the ion diamagnetic drift effect into account, the structures are slightly rotated with respect to the location of the helical core.
refers to the mode structure at the beginning of an oscillation cycle). Taking the ion diamagnetic drift effect into account, the structures are slightly rotated with respect to the location of the helical core.

Figure 13. Structures of $n^*=1$![]() mode for the two orthogonal solutions (a,b) without and (c,d) with taking the ion diamagnetic drift effect into account. The vectors characterise the velocity perturbation in the $R$
mode for the two orthogonal solutions (a,b) without and (c,d) with taking the ion diamagnetic drift effect into account. The vectors characterise the velocity perturbation in the $R$![]() –$Z$
–$Z$![]() plane at toroidal angle $\varphi =0^{\circ }$
plane at toroidal angle $\varphi =0^{\circ }$![]() and time $t=0$
and time $t=0$![]() .
.
(b) Diamagnetic drift effects change the Fourier composition of the eigenfunctions, as is illustrated for the $n^*=6$![]() mode in figure 14. There, we only show the radial velocity perturbation of the cosine-type function (Fourier coefficients of the complex and complex conjugate eigenfunctions have the same sign and size), because the sine-type function (Fourier coefficients of the complex and complex conjugate eigenfunctions have opposite signs) yields no new information. (This also holds for the imaginary part of the Fourier coefficients.) Without diamagnetic drift effects the complex and complex conjugate components of the Fourier spectrum are equal (see figure 14a). However, with diamagnetic drift effects the complex or complex conjugate components strongly dominate the Fourier spectrum (figure 14b). It is not only the diamagnetic drift effects that cause such a decoupling of the complex and complex conjugate parts of the eigenfunctions. This decoupling has also been observed in the case of toroidal plasma rotation as described in Puchmayr et al. (Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). Besides, figure 14(a) illustrates the coupling of many toroidal harmonics. There, the dominant $n$
mode in figure 14. There, we only show the radial velocity perturbation of the cosine-type function (Fourier coefficients of the complex and complex conjugate eigenfunctions have the same sign and size), because the sine-type function (Fourier coefficients of the complex and complex conjugate eigenfunctions have opposite signs) yields no new information. (This also holds for the imaginary part of the Fourier coefficients.) Without diamagnetic drift effects the complex and complex conjugate components of the Fourier spectrum are equal (see figure 14a). However, with diamagnetic drift effects the complex or complex conjugate components strongly dominate the Fourier spectrum (figure 14b). It is not only the diamagnetic drift effects that cause such a decoupling of the complex and complex conjugate parts of the eigenfunctions. This decoupling has also been observed in the case of toroidal plasma rotation as described in Puchmayr et al. (Reference Puchmayr, Dunne, Strumberger, Willensdorfer, Zohm and Hindenlang2023). Besides, figure 14(a) illustrates the coupling of many toroidal harmonics. There, the dominant $n$![]() cannot be identified. However, considering the perturbation in real space (see figure 14c), the $n^*=6$
cannot be identified. However, considering the perturbation in real space (see figure 14c), the $n^*=6$![]() character of the mode appears. Taking diamagnetic drift effects into account, the toroidal coupling is reduced. The $m/n=6/6$
character of the mode appears. Taking diamagnetic drift effects into account, the toroidal coupling is reduced. The $m/n=6/6$![]() harmonic yields the largest contribution to the Fourier spectrum of the perturbation shown in figure 14(b), while the contributions of the other $n$
harmonic yields the largest contribution to the Fourier spectrum of the perturbation shown in figure 14(b), while the contributions of the other $n$![]() harmonics are reduced. This reduction leads to a more uniformly distributed mode structure in the poloidal direction (see figure 14d). The coupling of the poloidal harmonics plays only a minor role for the mode structure, because of the very flat $q$
harmonics are reduced. This reduction leads to a more uniformly distributed mode structure in the poloidal direction (see figure 14d). The coupling of the poloidal harmonics plays only a minor role for the mode structure, because of the very flat $q$![]() -profile.
-profile.

Figure 14. (a,b) Fourier spectra of the real part of the radial velocity perturbation and (c,d) mode structures of the $n^*=6$![]() mode (a,c) without and (b,d) with ion diamagnetic drift effect. In (a,b) the solid and dashed lines denote the contributions of the complex and complex conjugate eigenfunctions, respectively. The largest contributions are marked by their poloidal and toroidal harmonics, $m/n$
mode (a,c) without and (b,d) with ion diamagnetic drift effect. In (a,b) the solid and dashed lines denote the contributions of the complex and complex conjugate eigenfunctions, respectively. The largest contributions are marked by their poloidal and toroidal harmonics, $m/n$![]() . In (c,d) the vectors characterise the velocity perturbation in the $R$
. In (c,d) the vectors characterise the velocity perturbation in the $R$![]() –$Z$
–$Z$![]() plane at toroidal angle $\varphi =0^{\circ }$
plane at toroidal angle $\varphi =0^{\circ }$![]() and time $t=0$
and time $t=0$![]() .
.
4. Summary and outlook
The 3-D linear resistive CASTOR3D code has been upgraded with respect to diamagnetic drift effects. The numerical results have been verified by comparing growth rates and oscillation frequencies computed with various coordinate types (see Appendix B). Furthermore, the presented results confirm previous findings (see e.g. Aiba Reference Aiba2016): (i) an ideal mode becomes stable when the absolute value of its oscillation frequency exceeds the corresponding ideal growth rate (the growth rate obtained without diamagnetic drift effects) and (ii) the oscillation frequency of an ideal mode agrees to a good approximation with half of the absolute value of the corresponding ion diamagnetic drift frequency, that is, $\omega \approx \omega _i^*/2$![]() .
.
Besides the standard approximations of equal pressures $p_i=p_e=0.5p$![]() or cold ions $p_i=0$
or cold ions $p_i=0$![]() , $p_e=p$
, $p_e=p$![]() , the CASTOR3D code allows any constant ratio of ion and electron pressures. The results show a strong dependence on this ratio. For ideal modes the stabilising diamagnetic drift effect decreases when the ion pressure is reduced, and is negligible for cold ions, because the ion diamagnetic drift effect is the major effect. In the case of resistive modes, however, both ion and electron diamagnetic drift effects are important. Their stabilising effects strongly depend on the ion/electron pressure ratio and the plasma resistivity. The oscillation frequencies of these modes agree very well with the corresponding ion diamagnetic drift frequencies, that is, $\omega \approx \omega _i^*$
, the CASTOR3D code allows any constant ratio of ion and electron pressures. The results show a strong dependence on this ratio. For ideal modes the stabilising diamagnetic drift effect decreases when the ion pressure is reduced, and is negligible for cold ions, because the ion diamagnetic drift effect is the major effect. In the case of resistive modes, however, both ion and electron diamagnetic drift effects are important. Their stabilising effects strongly depend on the ion/electron pressure ratio and the plasma resistivity. The oscillation frequencies of these modes agree very well with the corresponding ion diamagnetic drift frequencies, that is, $\omega \approx \omega _i^*$![]() . Eventually, the type of the most unstable mode may change when diamagnetic drift effects are taken into account. The types of the modes have been specified by analysing the corresponding ideal or resistive energy functional that has been determined from the solution of the eigenvalue problem without diamagnetic drift effects.
. Eventually, the type of the most unstable mode may change when diamagnetic drift effects are taken into account. The types of the modes have been specified by analysing the corresponding ideal or resistive energy functional that has been determined from the solution of the eigenvalue problem without diamagnetic drift effects.
Finally, the CASTOR3D code has been applied to a 3-D equilibrium, that is, a high-$\beta$![]() equilibrium with helical core. These first results obtained for ideal kink and interchange modes confirm: (i) the growing stabilising diamagnetic drift effect with increasing toroidal mode number (which is the dominant toroidal harmonic $n^*$
equilibrium with helical core. These first results obtained for ideal kink and interchange modes confirm: (i) the growing stabilising diamagnetic drift effect with increasing toroidal mode number (which is the dominant toroidal harmonic $n^*$![]() ) and (ii) the oscillation frequencies of the modes correspond to a good approximation to $\omega _i^*/2$
) and (ii) the oscillation frequencies of the modes correspond to a good approximation to $\omega _i^*/2$![]() . Besides these similarities with the high-$\beta$
. Besides these similarities with the high-$\beta$![]() axisymmetric equilibrium, additional effects have been found, namely: (i) sufficiently strong diamagnetic drift effects lead to a degeneration of otherwise non-degenerate growth rates, (ii) only modes with degenerate growth rates are able to oscillate and (iii) the diamagnetic drift effects change the composition of the eigenfunctions, that is, either the complex or the complex conjugate parts dominate the Fourier spectrum of the mode, and also the coupling of the toroidal harmonics is reduced leading to an alteration of the mode structure.
axisymmetric equilibrium, additional effects have been found, namely: (i) sufficiently strong diamagnetic drift effects lead to a degeneration of otherwise non-degenerate growth rates, (ii) only modes with degenerate growth rates are able to oscillate and (iii) the diamagnetic drift effects change the composition of the eigenfunctions, that is, either the complex or the complex conjugate parts dominate the Fourier spectrum of the mode, and also the coupling of the toroidal harmonics is reduced leading to an alteration of the mode structure.
While here simple test equilibria have been investigated to demonstrate the reliability of the CASTOR3D code, the code will be applied to realistic tokamak and stellarator equilibria next. Diamagnetic drift effects are, for example, of particular importance for MHD instabilities located in the pedestal region of H-mode plasmas (ELM stability). For this reason, an important application of the extended CASTOR3D code will be an investigation of how 3-D magnetic fields produced by magnetic perturbation coils, which are used for ELM control, change the linear MHD stability limits.
Acknowledgements
Editor Paolo Ricci thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (grant agreement no. 101052200-EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Ion diamagnetic drift frequency
The ion diamagnetic drift frequency $\omega _i^*={\boldsymbol V}_i^* \boldsymbol {\cdot } {\boldsymbol k}$![]() ($\boldsymbol k$
($\boldsymbol k$![]() is wavenumber vector) is a useful quantity for the discussion of diamagnetic drift effects. In Boozer coordinates ($s,v,u$
is wavenumber vector) is a useful quantity for the discussion of diamagnetic drift effects. In Boozer coordinates ($s,v,u$![]() ) the contravariant toroidal $V_i^{*v}$
) the contravariant toroidal $V_i^{*v}$![]() and poloidal $V_i^{*u}$
and poloidal $V_i^{*u}$![]() components of the ion drift velocity
components of the ion drift velocity

are constant on flux surfaces, because ion pressure $p_i$![]() , mass density $\rho$
, mass density $\rho$![]() , poloidal current $J$
, poloidal current $J$![]() , toroidal current $I$
, toroidal current $I$![]() and the derivatives of poloidal flux $\varPsi '$
and the derivatives of poloidal flux $\varPsi '$![]() and toroidal flux $\varPhi '$
and toroidal flux $\varPhi '$![]() depend only on the radial flux coordinate $s$
depend only on the radial flux coordinate $s$![]() . We approximate ${\boldsymbol k}$
. We approximate ${\boldsymbol k}$![]() by ${\boldsymbol k} = -{\rm i}({{\boldsymbol {\nabla }} f}/{f})$
by ${\boldsymbol k} = -{\rm i}({{\boldsymbol {\nabla }} f}/{f})$![]() , with function $f=f_0(s)\, \exp (2{\rm \pi} {\rm i}(mu-nv))$
, with function $f=f_0(s)\, \exp (2{\rm \pi} {\rm i}(mu-nv))$![]() . The latter describes the perturbation by the leading $m,n$
. The latter describes the perturbation by the leading $m,n$![]() Fourier harmonics. Then, we obtain for the ion diamagnetic drift frequency
Fourier harmonics. Then, we obtain for the ion diamagnetic drift frequency
Applying (A2) to the 1/1 modes of the high- and low-$\beta$![]() test equilibria, we get the ion diamagnetic drift frequencies shown in figure 15. There, we assumed $p_i=p_e$
test equilibria, we get the ion diamagnetic drift frequencies shown in figure 15. There, we assumed $p_i=p_e$![]() , that is, $\alpha _T=0.5$
, that is, $\alpha _T=0.5$![]() . The resulting absolute values of the ion diamagnetic drift frequencies amount to $|\omega _i^*|=5841$
. The resulting absolute values of the ion diamagnetic drift frequencies amount to $|\omega _i^*|=5841$![]() rad s$^{-1}$
rad s$^{-1}$![]() (high-$\beta$
(high-$\beta$![]() case) and $|\omega _i^*|=1947$
case) and $|\omega _i^*|=1947$![]() rad s$^{-1}$
rad s$^{-1}$![]() (low-$\beta$
(low-$\beta$![]() case) at the $\iota =1$
case) at the $\iota =1$![]() flux surface. There is no visible difference between the drift frequencies of the 2-D and 3-D high-$\beta$
flux surface. There is no visible difference between the drift frequencies of the 2-D and 3-D high-$\beta$![]() equilibria, because of the identical profiles and the small deviations between 2-D and 3-D flux surfaces. (Here the ion diamagnetic drift frequency is negative because of the used orientation of the magnetic field.)
equilibria, because of the identical profiles and the small deviations between 2-D and 3-D flux surfaces. (Here the ion diamagnetic drift frequency is negative because of the used orientation of the magnetic field.)

Figure 15. Ion diamagnetic drift frequency as a function of the square root of the normalised toroidal flux $s$![]() for a 1/1 mode and two volume-averaged $\beta$
for a 1/1 mode and two volume-averaged $\beta$![]() -values: $\langle \beta \rangle =2.96$
-values: $\langle \beta \rangle =2.96$![]() % (black solid line: 2-D equilibrium; red dashed line: 3-D equilibrium) and $\langle \beta \rangle =0.97$
% (black solid line: 2-D equilibrium; red dashed line: 3-D equilibrium) and $\langle \beta \rangle =0.97$![]() % (black solid line). The dotted vertical line marks the position of the $\iota =1$
% (black solid line). The dotted vertical line marks the position of the $\iota =1$![]() flux surface.
flux surface.
Appendix B. Numerical accuracy
The CASTOR3D code uses nested, non-orthogonal 3-D flux coordinates (Strumberger & Günter Reference Strumberger and Günter2017). Its general formulation allows the use of various coordinate types (e.g. NEMEC coordinates (Hirshman & Whitson Reference Hirshman and Whitson1983), Boozer coordinates (Boozer Reference Boozer1982) and 2-D straight field line coordinates (Huysmans et al. Reference Huysmans, Goedbloed and Kerner1993)). The latter are limited to axisymmetric equilibria. Using different coordinate types, errors in the formulation and/or implementation of the matrix elements, as well as a non-sufficient radial resolution or an unsuitable Fourier spectrum will lead to differing results. We therefore performed convergence studies with respect to Fourier spectra and radial grid resolutions for these three coordinate types and compared the results, in order to find the most appropriate ones.
Figures 16 and 17 show the almost perfect agreement of growth rates and oscillation frequencies obtained for ideal and resistive modes. Of course, only NEMEC and Boozer coordinates have been used in the case of the 3-D equilibrium (figure 16b). Concerning memory and computational time, 3-D calculations are much more expensive than 2-D calculations because of the toroidal mode coupling. Furthermore, they are more sensitive to numerical inaccuracies, so that non-physical ‘parasitic’ solutions and non-physical oscillations of the eigenfunctions increase with every physical effect that is additionally taken into account. Therefore, the computations presented in § 3.3 are restricted to the ion diamagnetic drift effect taken into account by the gyro-viscosity. Using NEMEC coordinates, however, we have been able to find several solutions taking ion and electron diamagnetic drift effects into account simultaneously. These results are additionally shown in figure 16(b). They confirm that neglecting the pressure terms in Ohm's law (2.14) is justified for the considered high-$\beta$![]() equilibrium.
equilibrium.

Figure 16. Growth rate $\gamma$![]() and absolute value of the oscillation frequency $|\omega |$
and absolute value of the oscillation frequency $|\omega |$![]() of the ideal modes as functions of the toroidal mode number $n$
of the ideal modes as functions of the toroidal mode number $n$![]() for (a) 2-D equilibrium, $\alpha _T=0.4$
for (a) 2-D equilibrium, $\alpha _T=0.4$![]() , and (b) 3-D equilibrium, $\alpha _T=0.5$
, and (b) 3-D equilibrium, $\alpha _T=0.5$![]() (NEMEC flux coordinates: black solid lines; Boozer coordinates: green crosses; 2-D straight field line coordinates: red circles). Here $\gamma _{{\rm ideal}}$
(NEMEC flux coordinates: black solid lines; Boozer coordinates: green crosses; 2-D straight field line coordinates: red circles). Here $\gamma _{{\rm ideal}}$![]() is the growth rate without taking diamagnetic drift effects into account. (a) Growth rate $\gamma$
is the growth rate without taking diamagnetic drift effects into account. (a) Growth rate $\gamma$![]() and $|\omega |$
and $|\omega |$![]() with ion and electron diamagnetic drift effects and (b) $\gamma$
with ion and electron diamagnetic drift effects and (b) $\gamma$![]() and $|\omega |$
and $|\omega |$![]() only with ion diamagnetic drift effect (black solid lines, green crosses) and with both effects (NEMEC coordinates: blue diamonds).
only with ion diamagnetic drift effect (black solid lines, green crosses) and with both effects (NEMEC coordinates: blue diamonds).

Figure 17. (a) Growth rate and (b) oscillation frequency as functions of the toroidal mode number (NEMEC flux coordinates: black solid line; straight field line coordinates: red circles; Boozer coordinates: green crosses) of the resistive modes with ion and electron diamagnetic drift effects.
There are several criteria to distinguish between non-physical and physical solutions. (a) Viewing the Fourier spectra of all perturbed quantities. In the case of non-physical solutions all Fourier spectra oscillate irregularly. (b) Making a scan over physical parameters (e.g. resistivity, toroidal mode number, etc.). The eigenvalues of non-physical solutions usually yield no smooth curves. (c) Making a scan over numerical parameters (e.g. number of radial grid points, number of Fourier harmonics, etc.). The eigenvalues of ‘parasitic’ solutions do not in general converge. They strongly depend on numerical parameters. (d) Using different coordinate types. Sometimes, a coordinate type produces more non-physical solutions than another one. While, ideally, physical solutions have almost identical eigenvalues in different coordinate systems (see figures 16 and 17), the ‘parasitic’ eigenvalues can usually not be reproduced with other coordinates. Together, these criteria allow one to identify the ‘parasitic’ solutions in most cases.