Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-04T19:41:59.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic solution for field-line reconnexion. Compressible case of Petschek's model†

Published online by Cambridge University Press:  13 March 2009

V. S. Semenov ,
I. V. Kubyshkin  and
M. F. Heyn
V. S. Semenov
Affiliation:
Institute of Physics, State University, Leningrad 198 904, USSR
I. V. Kubyshkin
Affiliation:
Institute of Physics, State University, Leningrad 198 904, USSR
M. F. Heyn
Affiliation:
Space Research Institute of the Austrian Academy of Sciences, c/oTechnical University Graz, Inffeldgasse 12, A-8010 Graz, Austria
Get access Rights & Permissions [Opens in a new window]

Abstract

For the solution of Petschek's problem of field-line reconnexion, a new method is elaborated which is based on the introduction of a special co-ordinate system in which the streamlines and the magnetic lines of force become co-ordinates simultaneously. We have constructed the zero-order and the first-order approximation (for small Alfvén Mach numbers) for the solution of Petschek's problem in the steady-state, compressible, two-dimensional symmetric case. It is shown that the density across the slow shock wave increases by a factor

and the pressure by

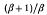
(β = 8πρ0/B20, γ being the adiabatic exponent), and the plasma accelerates up to the Alfvén velocity. On the bases of the results obtained and of the analysis of numerical experiments on the reconnexion problem we draw the conclusion that during the initial phase of the process there develops a current sheet as described by Syrovatskii and that simultaneously there is a development of the tearing mode instability whose nonlinear phase creates the condition for the reconnexion process in the sense of Petschek.

Type
Research Article
Information
Journal of Plasma Physics , Volume 30 , Issue 2 , October 1983 , pp. 303 - 320
Copyright
Copyright © Cambridge University Press 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Birn, J. 1980 J. Geophys. Res. 85, 1214.CrossRefGoogle Scholar
Brushlinskii, K. V., Zaborov, A. M. & Syrovatskii, S. I. 1980 Fiz. Plasmy, 6, 297.Google Scholar
Misner, O. W., Thorne, K. S. & Wheeler, J. A. 1973 Gravitation. Freemaan.Google Scholar
Petschek, H. E. 1964 Proceedings of AAS-NASA Symposium on the Physics of Solar Flares (ed. W. N. Hess). NASA SP-50, p. 425.Google Scholar
Pudovkin, M. I. & Semenov, V. S. 1977 Ann. Geophys. 33, 429.Google Scholar
Pushkar, E. A. 1976 Fluid Dynamics, 5, 755.Google Scholar
Sato, T. & Hayashi, T. 1979 Phys. Fluids, 22, 1189.CrossRefGoogle Scholar
Semenov, V. S. 1979 Geomagnitnaya Issledovantya, 24, 32.Google Scholar
Sonnerup, B. U. Ö. 1970 J. Plasma Phys. 4, 161.CrossRefGoogle Scholar
Sonnerup, B. U. Ö. 1979 Solar System Plasma Physics III (ed. Lanzerotti, L. J.Kennel, C. F. and Parker, E. N.), p. 45. North-Holland.Google Scholar
Sotov, B. V. & Syrovatskii, S. I. 1974 Trudy FIAN, 74, 14.Google Scholar
Soward, A. M. & Priest, E. R. 1977 Phil. Trans. Roy. Soc. A 284, 369.Google Scholar
Soward, A. M. & Priest, E. R. 1982 J. Plasma Phys. 28, 335.CrossRefGoogle Scholar
Tsuda, T. & Ugai, M. 1977 J. Plasma Phys. 18, 451.CrossRefGoogle Scholar
Vasyliunas, V. M. 1975 Rev. Geophys. Space Phys. 13, 303.CrossRefGoogle Scholar