1 Introduction
The nonlinear Compton scattering of high-intensity laser pulses off high-energy electrons is one of the fundamental processes in strong-field QED. Its theoretical description goes back to the 1960s where many strong-field QED processes had been studied in a series of seminal papers (Brown & Kibble Reference Brown and Kibble1964; Goldman Reference Goldman1964; Nikishov & Ritus Reference Nikishov and Ritus1964a
,Reference Nikishov and Ritus
b
, Reference Nikishov and Ritus1965). For instance, these authors predicted the emission of high harmonics and a nonlinear intensity-dependent redshift of the emitted radiation, which is proportional to
![]() $a_{0}^{2}$
, where
$a_{0}^{2}$
, where
![]() $a_{0}$
is the dimensionless normalized laser amplitude that is related to the laser intensity (
$a_{0}$
is the dimensionless normalized laser amplitude that is related to the laser intensity (
![]() $I$
) and wavelength (
$I$
) and wavelength (
![]() ${\it\lambda}$
) via
${\it\lambda}$
) via
![]() $a_{0}^{2}=0.73\times I~(10^{18}~\text{W}~\text{cm}^{-2})~{\it\lambda}^{2}~({\rm\mu}\text{m})$
. In a classical picture, the generation of high harmonics and the nonlinear redshift of the emitted radiation can be understood as the influence of the laser’s magnetic field due to the
$a_{0}^{2}=0.73\times I~(10^{18}~\text{W}~\text{cm}^{-2})~{\it\lambda}^{2}~({\rm\mu}\text{m})$
. In a classical picture, the generation of high harmonics and the nonlinear redshift of the emitted radiation can be understood as the influence of the laser’s magnetic field due to the
![]() $\boldsymbol{v}\times \boldsymbol{B}$
term in the classical Lorentz force equation.
$\boldsymbol{v}\times \boldsymbol{B}$
term in the classical Lorentz force equation.
However, while most contemporary high-intensity laser facilities generate laser pulses of femtosecond duration (Mourou, Tajima & Bulanov Reference Mourou, Tajima and Bulanov2006; Korzhimanov et al. Reference Korzhimanov, Gonoskov, Khazanov and Sergeev2011; Di Piazza et al. Reference Di Piazza, Müller, Hatsagortsyan and Keitel2012), most of the early papers on nonlinear Compton scattering did not consider the effect of the finite duration of the intense laser pulse. For a realistic laser pulse with a finite duration, the laser intensity gradually increases from zero to its maximum value. Consequently, the nonlinear redshift is not constant during the course of the laser pulse and the harmonic lines of the emitted radiation are considerably broadened, with a large number of spectral lines for each harmonic (Hartemann & Kerman Reference Hartemann and Kerman1996; Hartemann et al. Reference Hartemann, Troha, Luhmann and Toffano1996, Reference Hartemann, Albert, Craig and Barty2010; Narozhnyi & Fofanov Reference Narozhnyi and Fofanov1996; Boca & Florescu Reference Boca and Florescu2009; Mackenroth & Di Piazza Reference Mackenroth and Di Piazza2011; Seipt & Kämpfer Reference Seipt and Kämpfer2011; Dinu Reference Dinu2013). In the classical picture this broadening is caused by a gradual slowdown of the longitudinal electron motion as the laser intensity ramps up (Seipt et al. Reference Seipt, Rykovanov, Surzhykov and Fritzsche2015). The occurrence of the additional line structure can be interpreted as interference of the radiation that is emitted during different times (Seipt & Kämpfer Reference Seipt and Kämpfer2013b ). The broadening of the spectral lines is especially important with regard to the application of nonlinear Compton scattering as an X- and gamma-ray radiation source (Jochmann et al. Reference Jochmann, Irman, Bussmann, Couperus, Cowan, Debus, Kuntzsch, Ledingham, Lehnert and Sauerbrey2013; Rykovanov et al. Reference Rykovanov, Geddes, Vay, Schroeder, Esarey and Leemans2014; Sarri et al. Reference Sarri, Corvan, Schumaker, Cole, Di Piazza, Ahmed, Harvey, Keitel, Krushelnick and Mangles2014; Khrennikov et al. Reference Khrennikov, Wenz, Buck, Xu, Heigoldt, Veisz and Karsch2015; Seipt et al. Reference Seipt, Rykovanov, Surzhykov and Fritzsche2015).
For ultra-high laser intensities
![]() $a_{0}\gg 1$
the formation time of the emitted photon is much shorter than the laser period and the interference of radiation that is emitted at different times during the course of the pulse is suppressed (Dinu et al.
Reference Dinu, Harvey, Ilderton, Marklund and Torgrimsson2015). In this regime, where the Compton emission becomes vital for the formation of QED cascades, the spectrum can be effectively simulated using the photon emission probabilities in a constant crossed field (Ritus Reference Ritus1985; Fedotov et al.
Reference Fedotov, Narozhny, Mourou and Korn2010; King, Elkina & Ruhl Reference King, Elkina and Ruhl2013; Harvey, Ilderton & King Reference Harvey, Ilderton and King2015; Narozhny & Fedotov Reference Narozhny and Fedotov2015). We therefore focus in this paper on the intermediate-intensity region
$a_{0}\gg 1$
the formation time of the emitted photon is much shorter than the laser period and the interference of radiation that is emitted at different times during the course of the pulse is suppressed (Dinu et al.
Reference Dinu, Harvey, Ilderton, Marklund and Torgrimsson2015). In this regime, where the Compton emission becomes vital for the formation of QED cascades, the spectrum can be effectively simulated using the photon emission probabilities in a constant crossed field (Ritus Reference Ritus1985; Fedotov et al.
Reference Fedotov, Narozhny, Mourou and Korn2010; King, Elkina & Ruhl Reference King, Elkina and Ruhl2013; Harvey, Ilderton & King Reference Harvey, Ilderton and King2015; Narozhny & Fedotov Reference Narozhny and Fedotov2015). We therefore focus in this paper on the intermediate-intensity region
![]() $a_{0}\sim 1$
, where the interference matters and a general relation between the shape and duration of the laser pulse and the shape of the spectrum of the backscattered light is very complicated and highly nonlinear. The shape of the harmonic lines is determined by an interplay between the laser pulse duration, (i) spectral composition of the pulse and (ii) the nonlinear ponderomotive broadening which depends on the laser intensity ramps.
$a_{0}\sim 1$
, where the interference matters and a general relation between the shape and duration of the laser pulse and the shape of the spectrum of the backscattered light is very complicated and highly nonlinear. The shape of the harmonic lines is determined by an interplay between the laser pulse duration, (i) spectral composition of the pulse and (ii) the nonlinear ponderomotive broadening which depends on the laser intensity ramps.
In this paper we analytically analyse the nonlinear Compton scattering process in a short intense plane wave laser pulse of circular polarization. Our analysis is based on the framework of strong-field QED, where the electrons are described as Volkov states, and we employ the slowly varying envelope approximation. For convenience, the analysis is performed in the incident electron frame of reference. In particular, we investigate how the duration and the shape of the short intense laser pulse affect the spectrum of the emitted radiation. We derive a scale-invariant master integral that contains all dependencies on the shape of the laser pulse, and we give explicit analytical expressions for several specific laser pulse shapes. Our paper is organized as follows: in § 2 we briefly outline the calculation of the transition amplitude and the energy and angular-differential emission probability for nonlinear Compton scattering using Volkov states in a pulsed laser field. The transition amplitude is analysed further in § 3 where we extract the dependence on the duration and shape of the laser pulse in the form of a master integral. Explicit analytic expressions for the master integrals for different pulse shapes are given in § 3.4. Throughout the paper we use units with
![]() $\hslash =c=1$
. Scalar products between four-vectors are denoted by
$\hslash =c=1$
. Scalar products between four-vectors are denoted by
![]() $a\cdot b\equiv a^{{\it\mu}}b_{{\it\mu}}=a^{0}b^{0}-\boldsymbol{a}\boldsymbol{b}$
, and the Feynman slash notation is used for scalar products between four-vectors and the Dirac matrices:
$a\cdot b\equiv a^{{\it\mu}}b_{{\it\mu}}=a^{0}b^{0}-\boldsymbol{a}\boldsymbol{b}$
, and the Feynman slash notation is used for scalar products between four-vectors and the Dirac matrices:
![]() $\cancel{a}\equiv {\it\gamma}\cdot a$
.
$\cancel{a}\equiv {\it\gamma}\cdot a$
.
2 Theoretical background
The nonlinear Compton scattering process, i.e. the emission of a photon by an electron under the action of an intense laser field, is conveniently described theoretically in the Furry picture. The interaction of the electrons with the laser pulse is treated non-perturbatively by using Volkov electron states
![]() ${\it\Psi}$
as solutions of the Dirac equation
${\it\Psi}$
as solutions of the Dirac equation
![]() $(\text{i}\cancel{\partial }-e\cancel{A}-m){\it\Psi}=0$
in the plane wave background laser field
$(\text{i}\cancel{\partial }-e\cancel{A}-m){\it\Psi}=0$
in the plane wave background laser field
![]() $A$
. Here
$A$
. Here
![]() $m$
and
$m$
and
![]() $e=-|e|$
denote the mass and charge of the electron, respectively. By employing these Volkov states, the strong-field
$e=-|e|$
denote the mass and charge of the electron, respectively. By employing these Volkov states, the strong-field
![]() $\unicode[STIX]{x1D64E}$
matrix in the Furry picture can be represented by the Feynman diagram in figure 1. It is given by the expression
$\unicode[STIX]{x1D64E}$
matrix in the Furry picture can be represented by the Feynman diagram in figure 1. It is given by the expression
where
![]() ${\mathcal{A}}_{k^{\prime }}^{{\it\mu}}(x)=({\it\varepsilon}^{\prime \ast })^{{\it\mu}}\text{e}^{\text{i}k^{\prime }\cdot x}$
is the amplitude for the emission of a (non-laser) photon with four-momentum
${\mathcal{A}}_{k^{\prime }}^{{\it\mu}}(x)=({\it\varepsilon}^{\prime \ast })^{{\it\mu}}\text{e}^{\text{i}k^{\prime }\cdot x}$
is the amplitude for the emission of a (non-laser) photon with four-momentum
![]() $k^{\prime }$
and polarization
$k^{\prime }$
and polarization
![]() ${\it\varepsilon}^{\prime }$
, while
${\it\varepsilon}^{\prime }$
, while
![]() $p$
and
$p$
and
![]() $p^{\prime }$
are the asymptotic four-momenta of the electron before and after the photon emission.
$p^{\prime }$
are the asymptotic four-momenta of the electron before and after the photon emission.

Figure 1. Feynman diagram for the emission of a photon with four-momentum
![]() $k^{\prime }$
(wiggly line) by a laser-dressed Volkov electron with asymptotic four-momentum
$k^{\prime }$
(wiggly line) by a laser-dressed Volkov electron with asymptotic four-momentum
![]() $p$
(double-line). After the photon emission the electron has the asymptotic four-momentum
$p$
(double-line). After the photon emission the electron has the asymptotic four-momentum
![]() $p^{\prime }$
. The double-lines indicate the non-perturbative interaction of the electron with the intense short laser pulse.
$p^{\prime }$
. The double-lines indicate the non-perturbative interaction of the electron with the intense short laser pulse.
In the following, we shall restrict our discussion to the case of a circularly polarized laser pulse with the four-vector potential in the axial gauge (
![]() $k\cdot A=0$
)
$k\cdot A=0$
)
It depends only on the phase variable
![]() ${\it\phi}=k\cdot x$
with the laser photon four-momentum
${\it\phi}=k\cdot x$
with the laser photon four-momentum
![]() $k=({\it\omega},0,0,-{\it\omega})$
, and with the normalized polarization four-vector
$k=({\it\omega},0,0,-{\it\omega})$
, and with the normalized polarization four-vector
![]() ${\it\epsilon}_{\pm }^{{\it\mu}}=(0,1,\pm \text{i},0)/\sqrt{2}$
, with
${\it\epsilon}_{\pm }^{{\it\mu}}=(0,1,\pm \text{i},0)/\sqrt{2}$
, with
![]() ${\it\epsilon}_{+}\cdot {\it\epsilon}_{-}=-1$
. The dimensionless normalized laser amplitude is given by
${\it\epsilon}_{+}\cdot {\it\epsilon}_{-}=-1$
. The dimensionless normalized laser amplitude is given by
![]() $a_{0}=|e|A_{0}/m$
. The shape of the laser pulse is described by an envelope function
$a_{0}=|e|A_{0}/m$
. The shape of the laser pulse is described by an envelope function
![]() $g({\it\phi})$
, that depends on
$g({\it\phi})$
, that depends on
![]() ${\it\phi}$
only via the ratio
${\it\phi}$
only via the ratio
![]() ${\it\phi}/{\rm\Delta}{\it\phi}$
with the pulse duration
${\it\phi}/{\rm\Delta}{\it\phi}$
with the pulse duration
![]() ${\rm\Delta}{\it\phi}$
. Moreover, we use symmetric pulse envelopes with
${\rm\Delta}{\it\phi}$
. Moreover, we use symmetric pulse envelopes with
![]() $g({\it\phi})=g(-{\it\phi})$
,
$g({\it\phi})=g(-{\it\phi})$
,
![]() $g(0)=1$
and
$g(0)=1$
and
![]() $g(\pm \infty )=0$
. For the following we shall assume that the laser pulse consists of several optical cycles such that
$g(\pm \infty )=0$
. For the following we shall assume that the laser pulse consists of several optical cycles such that
![]() ${\rm\Delta}{\it\phi}\gg 1$
and we may employ the slowly varying envelope approximation.
${\rm\Delta}{\it\phi}\gg 1$
and we may employ the slowly varying envelope approximation.
One can perform the spatial integrations in the
![]() $\unicode[STIX]{x1D64E}$
matrix most conveniently in light-front coordinates, defined as
$\unicode[STIX]{x1D64E}$
matrix most conveniently in light-front coordinates, defined as
![]() $x^{\pm }=x^{0}\pm x^{3}$
and
$x^{\pm }=x^{0}\pm x^{3}$
and
![]() $\boldsymbol{x}^{\bot }=(x^{1},x^{2})$
, such that the laser phase is proportional to
$\boldsymbol{x}^{\bot }=(x^{1},x^{2})$
, such that the laser phase is proportional to
![]() ${\it\phi}={\it\omega}x^{+}$
, and
${\it\phi}={\it\omega}x^{+}$
, and
![]() $\text{d}^{4}x=(2{\it\omega})^{-1}\,\text{d}{\it\phi}\,\text{d}x^{-}\text{d}^{2}\boldsymbol{x}^{\bot }$
. After integrating over three light-front coordinates, the
$\text{d}^{4}x=(2{\it\omega})^{-1}\,\text{d}{\it\phi}\,\text{d}x^{-}\text{d}^{2}\boldsymbol{x}^{\bot }$
. After integrating over three light-front coordinates, the
![]() $\unicode[STIX]{x1D64E}$
matrix can be represented in a form (Seipt & Kämpfer Reference Seipt and Kämpfer2013a
)
$\unicode[STIX]{x1D64E}$
matrix can be represented in a form (Seipt & Kämpfer Reference Seipt and Kämpfer2013a
)
with the light-front delta function
![]() ${\it\delta}_{l.f.}(p-p^{\prime }-k^{\prime })=(1/{\it\omega}){\it\delta}^{2}(\boldsymbol{p}_{\bot }-\boldsymbol{p}_{\bot }^{\prime }-\boldsymbol{k}_{\bot }^{\prime }){\it\delta}(p^{+}-p^{\prime +}-k^{\prime +})$
, enforcing the conservation of three momentum components, and the transition amplitude
${\it\delta}_{l.f.}(p-p^{\prime }-k^{\prime })=(1/{\it\omega}){\it\delta}^{2}(\boldsymbol{p}_{\bot }-\boldsymbol{p}_{\bot }^{\prime }-\boldsymbol{k}_{\bot }^{\prime }){\it\delta}(p^{+}-p^{\prime +}-k^{\prime +})$
, enforcing the conservation of three momentum components, and the transition amplitude
Here, the quantities
![]() $\mathscr{T}_{j}$
denote the transition operators
$\mathscr{T}_{j}$
denote the transition operators
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{T}_{0}=\bar{u}_{p^{\prime }}\cancel{{\it\varepsilon}}^{\prime \ast }u_{p},\\ \displaystyle \mathscr{T}_{\pm }=\frac{ma_{0}}{4}\bar{u}_{p^{\prime }}\left(\frac{\cancel{{\it\varepsilon}}_{\pm }\cancel{k}\cancel{{\it\varepsilon}}^{\prime \ast }}{(k\cdot p^{\prime })}+\frac{\cancel{{\it\varepsilon}}^{\prime \ast }\cancel{k}\cancel{{\it\varepsilon}}_{\pm }}{(k\cdot p)}\right)u_{p},\\ \displaystyle \mathscr{T}_{2}=\frac{m^{2}a_{0}^{2}({\it\varepsilon}^{\prime \ast }\cdot k)}{4(k\cdot p)(k\cdot p^{\prime })}\bar{u}_{p^{\prime }}\cancel{k}u_{p},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{T}_{0}=\bar{u}_{p^{\prime }}\cancel{{\it\varepsilon}}^{\prime \ast }u_{p},\\ \displaystyle \mathscr{T}_{\pm }=\frac{ma_{0}}{4}\bar{u}_{p^{\prime }}\left(\frac{\cancel{{\it\varepsilon}}_{\pm }\cancel{k}\cancel{{\it\varepsilon}}^{\prime \ast }}{(k\cdot p^{\prime })}+\frac{\cancel{{\it\varepsilon}}^{\prime \ast }\cancel{k}\cancel{{\it\varepsilon}}_{\pm }}{(k\cdot p)}\right)u_{p},\\ \displaystyle \mathscr{T}_{2}=\frac{m^{2}a_{0}^{2}({\it\varepsilon}^{\prime \ast }\cdot k)}{4(k\cdot p)(k\cdot p^{\prime })}\bar{u}_{p^{\prime }}\cancel{k}u_{p},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
which are sensitive to the spin of the incident and final electrons (via the spinors
![]() $u_{p}$
and
$u_{p}$
and
![]() $\bar{u}_{p^{\prime }}$
) and the polarization of the emitted photon. However, they are only weakly dependent on the energy and momentum of the emitted photon. The dependence on the dynamics of the scattering process is mainly contained in the so-called dynamic integrals over the laser phase
$\bar{u}_{p^{\prime }}$
) and the polarization of the emitted photon. However, they are only weakly dependent on the energy and momentum of the emitted photon. The dependence on the dynamics of the scattering process is mainly contained in the so-called dynamic integrals over the laser phase
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{C}_{\pm 1}=\int _{-\infty }^{\infty }\text{d}{\it\phi}g({\it\phi})\text{e}^{\mp \text{i}{\it\phi}}\exp \left\{\text{i}\ell \left[{\it\phi}+{\it\alpha}g({\it\phi})\sin ({\it\phi}+{\it\varphi})+{\it\beta}\int _{0}^{{\it\phi}}\text{d}{\it\phi}^{\prime }g^{2}({\it\phi}^{\prime })\right]\right\},\\ \displaystyle \mathscr{C}_{2}=\int _{-\infty }^{\infty }\text{d}{\it\phi}g^{2}({\it\phi})\exp \left\{\text{i}\ell \left[{\it\phi}+{\it\alpha}g({\it\phi})\sin ({\it\phi}+{\it\varphi})+{\it\beta}\int _{0}^{{\it\phi}}\,\text{d}{\it\phi}^{\prime }g^{2}({\it\phi}^{\prime })\right]\right\}.\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{C}_{\pm 1}=\int _{-\infty }^{\infty }\text{d}{\it\phi}g({\it\phi})\text{e}^{\mp \text{i}{\it\phi}}\exp \left\{\text{i}\ell \left[{\it\phi}+{\it\alpha}g({\it\phi})\sin ({\it\phi}+{\it\varphi})+{\it\beta}\int _{0}^{{\it\phi}}\text{d}{\it\phi}^{\prime }g^{2}({\it\phi}^{\prime })\right]\right\},\\ \displaystyle \mathscr{C}_{2}=\int _{-\infty }^{\infty }\text{d}{\it\phi}g^{2}({\it\phi})\exp \left\{\text{i}\ell \left[{\it\phi}+{\it\alpha}g({\it\phi})\sin ({\it\phi}+{\it\varphi})+{\it\beta}\int _{0}^{{\it\phi}}\,\text{d}{\it\phi}^{\prime }g^{2}({\it\phi}^{\prime })\right]\right\}.\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
Here we employ the slowly varying envelope approximation for the laser pulse and we use the definition
![]() ${\it\varphi}=\arctan k_{y}^{\prime }/k_{x}^{\prime }$
. The fourth dynamic integral
${\it\varphi}=\arctan k_{y}^{\prime }/k_{x}^{\prime }$
. The fourth dynamic integral
![]() $\mathscr{C}_{0}$
is represented as a combination of the other three integrals, defined in (2.6), as
$\mathscr{C}_{0}$
is represented as a combination of the other three integrals, defined in (2.6), as
by the requirement of the gauge invariance of the
![]() $\unicode[STIX]{x1D64E}$
matrix (Ilderton Reference Ilderton2011; Seipt Reference Seipt2012).
$\unicode[STIX]{x1D64E}$
matrix (Ilderton Reference Ilderton2011; Seipt Reference Seipt2012).
Here we have defined
![]() $\ell$
as the amount of four-momentum that is absorbed from the laser field
$\ell$
as the amount of four-momentum that is absorbed from the laser field
and provides a Lorentz-invariant way to parametrise the frequency of the emitted photon
For convenience, we move to the rest frame of the incident electron, where
![]() $p=(m,0,0,0)$
. Moreover, we defined the coefficients
$p=(m,0,0,0)$
. Moreover, we defined the coefficients
Using the the transition amplitude (2.4), the angular- and energy-differential photon emission probability is given by (Seipt & Kämpfer Reference Seipt and Kämpfer2011; Seipt Reference Seipt2012)
In order to study how the differential emission probability depends on the laser pulse parameters – the laser strength
![]() $a_{0}$
, pulse duration
$a_{0}$
, pulse duration
![]() ${\rm\Delta}{\it\phi}$
or the shape of the pulse envelope
${\rm\Delta}{\it\phi}$
or the shape of the pulse envelope
![]() $g$
– it is required to evaluate the dynamic integrals
$g$
– it is required to evaluate the dynamic integrals
![]() $\mathscr{C}_{j}$
.
$\mathscr{C}_{j}$
.
For many purposes it is sufficient to perform the integrations over the laser phase numerically, as was done for instance in Mackenroth & Di Piazza (Reference Mackenroth and Di Piazza2011), Seipt & Kämpfer (Reference Seipt and Kämpfer2011), Krajewska & Kamiński (Reference Krajewska and Kamiński2012) and Twardy, Krajewska & Kamiński (Reference Twardy, Krajewska and Kamiński2014). Another approach to calculate the spectrum (2.12) relies on a saddle point analysis of the highly oscillating phase integrals in (2.6) (Narozhnyi & Fofanov Reference Narozhnyi and Fofanov1996; Mackenroth, Di Piazza & Keitel Reference Mackenroth, Di Piazza and Keitel2010; Seipt & Kämpfer Reference Seipt and Kämpfer2013b ; Seipt et al. Reference Seipt, Rykovanov, Surzhykov and Fritzsche2015, Reference Seipt, Surzhykov, Fritzsche and Kämpfer2016). A third possibility to evaluate the dynamic integrals would be an attempt to find analytic solutions. Such a completely analytical evaluation has been done for instance in (Hartemann et al. Reference Hartemann, Troha, Luhmann and Toffano1996) for the on-axis radiation spectrum using classical electrodynamics. This approach will be pursued in this paper for arbitrary emission angles and general pulse shapes. In the following we will present a completely analytical evaluation of the dynamic integrals to gain more insight into the dependence of the spectrum of the backscattered light on the laser pulse duration and envelope shape.
3 Analytic evaluation of the dynamic integrals
In this section we further analyse the properties of the spectrum of the emitted radiation. We apply a detailed mathematical analysis to the transition amplitude
![]() $\mathscr{M}$
, and in particular the dynamic integrals
$\mathscr{M}$
, and in particular the dynamic integrals
![]() $\mathscr{C}_{j}$
, from the previous section in order to extract how they depend on the laser pulse duration and pulse shape. Here, we aim to provide explicit analytic expressions for the dynamic integrals (2.6).
$\mathscr{C}_{j}$
, from the previous section in order to extract how they depend on the laser pulse duration and pulse shape. Here, we aim to provide explicit analytic expressions for the dynamic integrals (2.6).
It is known from previous studies (Narozhnyi & Fofanov Reference Narozhnyi and Fofanov1996; Seipt & Kämpfer Reference Seipt and Kämpfer2013b
; Seipt et al.
Reference Seipt, Rykovanov, Surzhykov and Fritzsche2015) that the oscillating term (
![]() $\propto {\it\alpha}$
) in the exponent of the dynamic integrals, (2.6), is responsible for the emission of high harmonics. The term containing the integral over the squared pulse envelope (
$\propto {\it\alpha}$
) in the exponent of the dynamic integrals, (2.6), is responsible for the emission of high harmonics. The term containing the integral over the squared pulse envelope (
![]() $\propto {\it\beta}$
) changes only slowly as a function of
$\propto {\it\beta}$
) changes only slowly as a function of
![]() ${\it\phi}$
. This so-called ponderomotive term is responsible for the broadening of the harmonic lines and the spectral structures seen within each harmonic. In the following, we first disentangle these two effects (§ 3.1) and later analyse the ponderomotive broadening for each harmonic line (§§ 3.2 et seq.)
${\it\phi}$
. This so-called ponderomotive term is responsible for the broadening of the harmonic lines and the spectral structures seen within each harmonic. In the following, we first disentangle these two effects (§ 3.1) and later analyse the ponderomotive broadening for each harmonic line (§§ 3.2 et seq.)
3.1 Expansion into harmonics
Let us first expand the dynamic integrals into a sum of partial terms which can be interpreted as the emission of higher harmonics in analogy to the case of infinite plane waves. Following Narozhnyi & Fofanov (Reference Narozhnyi and Fofanov1996) and Seipt & Kämpfer (Reference Seipt and Kämpfer2013b
), we define a generalized floating window Fourier series for a non-periodic function
![]() $f({\it\phi})$
$f({\it\phi})$
with Fourier coefficients
![]() $c_{n}({\it\phi})$
that depend on the location of the window centre. Applying this floating window Fourier series to the integrand of the dynamic integrals, and using the slowly varying envelope approximation (Narozhnyi & Fofanov Reference Narozhnyi and Fofanov1996), yields a generalized Jacobi–Anger type expansion
$c_{n}({\it\phi})$
that depend on the location of the window centre. Applying this floating window Fourier series to the integrand of the dynamic integrals, and using the slowly varying envelope approximation (Narozhnyi & Fofanov Reference Narozhnyi and Fofanov1996), yields a generalized Jacobi–Anger type expansion
with the Bessel function of the first kind
![]() $\text{J}_{n}(z)$
(Watson Reference Watson1922). This expansion strongly resembles the expansion into harmonics known from the well-studied case of infinite plane waves (Berestetzki, Lifschitz & Pitajewski Reference Berestetzki, Lifschitz and Pitajewski1980), where
$\text{J}_{n}(z)$
(Watson Reference Watson1922). This expansion strongly resembles the expansion into harmonics known from the well-studied case of infinite plane waves (Berestetzki, Lifschitz & Pitajewski Reference Berestetzki, Lifschitz and Pitajewski1980), where
![]() $g=1$
. Note, however, that here the argument of the Bessel functions depends on the laser phase
$g=1$
. Note, however, that here the argument of the Bessel functions depends on the laser phase
![]() ${\it\phi}$
via laser pulse envelope
${\it\phi}$
via laser pulse envelope
![]() $g({\it\phi})$
.
$g({\it\phi})$
.
Employing the above expansion we can cast the dynamic integrals into a form
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{C}_{2}(\ell )=\mathop{\sum }_{n}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}C_{2}^{(n)}(\ell ),\\ \displaystyle \mathscr{C}_{\pm }(\ell )=\mathop{\sum }_{n}(-1)^{n}\text{e}^{-\text{i}(n\mp 1){\it\varphi}}C_{\pm }^{(n)}(\ell ),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathscr{C}_{2}(\ell )=\mathop{\sum }_{n}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}C_{2}^{(n)}(\ell ),\\ \displaystyle \mathscr{C}_{\pm }(\ell )=\mathop{\sum }_{n}(-1)^{n}\text{e}^{-\text{i}(n\mp 1){\it\varphi}}C_{\pm }^{(n)}(\ell ),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle C_{2}^{(n)}(\ell )=\int _{-\infty }^{\infty }\text{d}{\it\phi}g^{2}({\it\phi})\text{J}_{n}(\ell {\it\alpha}g)\text{e}^{\text{i}(\ell -n){\it\phi}+\text{i}\ell {\it\beta}\int \,\text{d}{\it\phi}g^{2}},\\ \displaystyle C_{\pm }^{(n)}(\ell )=\int _{-\infty }^{\infty }\text{d}{\it\phi}g({\it\phi})\text{J}_{n\mp 1}(\ell {\it\alpha}g)\text{e}^{\text{i}(\ell -n){\it\phi}+\text{i}\ell {\it\beta}\int \text{d}{\it\phi}g^{2}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle C_{2}^{(n)}(\ell )=\int _{-\infty }^{\infty }\text{d}{\it\phi}g^{2}({\it\phi})\text{J}_{n}(\ell {\it\alpha}g)\text{e}^{\text{i}(\ell -n){\it\phi}+\text{i}\ell {\it\beta}\int \,\text{d}{\it\phi}g^{2}},\\ \displaystyle C_{\pm }^{(n)}(\ell )=\int _{-\infty }^{\infty }\text{d}{\it\phi}g({\it\phi})\text{J}_{n\mp 1}(\ell {\it\alpha}g)\text{e}^{\text{i}(\ell -n){\it\phi}+\text{i}\ell {\it\beta}\int \text{d}{\it\phi}g^{2}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Note that for symmetric laser pulse envelopes, as we use in this paper, all the coefficients
![]() $C_{j}^{(n)}(\ell )$
are purely real valued. Making use of the expansions (3.3), the transition amplitude
$C_{j}^{(n)}(\ell )$
are purely real valued. Making use of the expansions (3.3), the transition amplitude
![]() $\mathscr{M}$
can be written as a sum of partial amplitudes
$\mathscr{M}$
can be written as a sum of partial amplitudes
![]() $\mathscr{M}^{(n)}$
via
$\mathscr{M}^{(n)}$
via
![]() $\mathscr{M}=\sum _{n=1}^{\infty }\mathscr{M}^{(n)}$
, representing the emission of the
$\mathscr{M}=\sum _{n=1}^{\infty }\mathscr{M}^{(n)}$
, representing the emission of the
![]() $n$
th harmonic. The shape of each of the harmonic lines is determined by the integrals
$n$
th harmonic. The shape of each of the harmonic lines is determined by the integrals
![]() $C_{j}^{(n)}(\ell )$
, which might be called the partial dynamic integrals for the
$C_{j}^{(n)}(\ell )$
, which might be called the partial dynamic integrals for the
![]() $n$
th harmonic. Unfortunately, in these integrals, the pulse envelope
$n$
th harmonic. Unfortunately, in these integrals, the pulse envelope
![]() $g$
appears as the argument of the Bessel function, preventing their immediate analytic evaluation.
$g$
appears as the argument of the Bessel function, preventing their immediate analytic evaluation.
The parameter
![]() ${\it\alpha}$
that appears in the argument of the Bessel functions goes to zero for on-axis radiation,
${\it\alpha}$
that appears in the argument of the Bessel functions goes to zero for on-axis radiation,
![]() ${\it\vartheta}=0$
. Since the Bessel functions behave as
${\it\vartheta}=0$
. Since the Bessel functions behave as
![]() $\text{J}_{n}(z)\approx z^{n}/2^{n}n!$
for small argument
$\text{J}_{n}(z)\approx z^{n}/2^{n}n!$
for small argument
![]() $z$
this means that only the first harmonic
$z$
this means that only the first harmonic
![]() $n=1$
is emitted on axis for a circularly polarized laser pulse, with the only contribution coming from
$n=1$
is emitted on axis for a circularly polarized laser pulse, with the only contribution coming from
![]() $C_{+}^{(1)}$
. The result that no higher harmonics occur on axis is known from the case of infinitely long plane waves as a ‘blind spot’ or ‘dead cone’ in the literature (see e.g. Harvey, Heinzl & Ilderton (Reference Harvey, Heinzl and Ilderton2009) and references therein).
$C_{+}^{(1)}$
. The result that no higher harmonics occur on axis is known from the case of infinitely long plane waves as a ‘blind spot’ or ‘dead cone’ in the literature (see e.g. Harvey, Heinzl & Ilderton (Reference Harvey, Heinzl and Ilderton2009) and references therein).
3.2 Reduction to a master integral
The next important step is to extract the pulse shape function
![]() $g$
from the argument of the Bessel functions in the definition of the integrals
$g$
from the argument of the Bessel functions in the definition of the integrals
![]() $C_{j}^{(n)}$
. This will eventually allow us to define a master integral that contains all of the dependences on the laser pulse envelope. Such an extraction is achieved by applying the multiple argument expansion for the Bessel functions (Watson Reference Watson1922)
$C_{j}^{(n)}$
. This will eventually allow us to define a master integral that contains all of the dependences on the laser pulse envelope. Such an extraction is achieved by applying the multiple argument expansion for the Bessel functions (Watson Reference Watson1922)
Thus, instead of having to deal with the pulse envelope
![]() $g$
as an argument of the
$g$
as an argument of the
![]() $n$
th Bessel function we now get a power series in
$n$
th Bessel function we now get a power series in
![]() $(1-g^{2})$
, with the coefficients containing higher-order Bessel functions. We should note that the overlap of the functions
$(1-g^{2})$
, with the coefficients containing higher-order Bessel functions. We should note that the overlap of the functions
![]() $g^{n}$
and some power of
$g^{n}$
and some power of
![]() $(1-g^{2})^{k}$
rapidly becomes small for increasing
$(1-g^{2})^{k}$
rapidly becomes small for increasing
![]() $n$
and
$n$
and
![]() $k$
. The powers of
$k$
. The powers of
![]() $g^{n}$
are localized at the origin
$g^{n}$
are localized at the origin
![]() ${\it\phi}=0$
more strongly for larger values of
${\it\phi}=0$
more strongly for larger values of
![]() $n$
, while the powers of
$n$
, while the powers of
![]() $(1-g^{2})$
vanish at the origin. Their product in the expansion (3.5) samples the edges of the laser pulse.
$(1-g^{2})$
vanish at the origin. Their product in the expansion (3.5) samples the edges of the laser pulse.
Employing the above expansions we obtain for the partial dynamic integrals for the
![]() $n$
th harmonic the series
$n$
th harmonic the series
They contain all dependences on the laser pulse shape and pulse duration and its influence on the longitudinal electron motion and spectral broadening.
Before evaluating these ponderomotive integrals further, let us first discuss the limit of infinite plane waves,
![]() $g\rightarrow 1$
, where the laser intensity is switched on adiabatically at past infinity and then stays constant. As a consequence there is no ponderomotive broadening for infinite plane waves. Because of
$g\rightarrow 1$
, where the laser intensity is switched on adiabatically at past infinity and then stays constant. As a consequence there is no ponderomotive broadening for infinite plane waves. Because of
![]() $1-g^{2}=0$
we find
$1-g^{2}=0$
we find
The delta function here restricts the generally continuous variable
![]() $\ell$
to discrete values
$\ell$
to discrete values
![]() $\ell _{n}=n/(1+{\it\beta})$
. Thus, the frequency of the emitted photon, (2.9), becomes discrete as well:
$\ell _{n}=n/(1+{\it\beta})$
. Thus, the frequency of the emitted photon, (2.9), becomes discrete as well:
 $$\begin{eqnarray}\displaystyle {\it\omega}_{n}^{\prime }\equiv {\it\omega}^{\prime }(\ell _{n})=\frac{n{\it\omega}}{1+{\it\beta}+\displaystyle \frac{n{\it\omega}}{m}(1+\cos {\it\vartheta})}=\frac{n{\it\omega}}{1+\displaystyle \left(\frac{n{\it\omega}}{m}+\frac{a_{0}^{2}}{4}\right)(1+\cos {\it\vartheta})}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\omega}_{n}^{\prime }\equiv {\it\omega}^{\prime }(\ell _{n})=\frac{n{\it\omega}}{1+{\it\beta}+\displaystyle \frac{n{\it\omega}}{m}(1+\cos {\it\vartheta})}=\frac{n{\it\omega}}{1+\displaystyle \left(\frac{n{\it\omega}}{m}+\frac{a_{0}^{2}}{4}\right)(1+\cos {\it\vartheta})}, & & \displaystyle\end{eqnarray}$$
with the well-known nonlinear intensity dependent redshift (Berestetzki et al.
Reference Berestetzki, Lifschitz and Pitajewski1980), but no spectral broadening. Equation (3.10) is usually interpreted as the absorption of
![]() $n$
laser photons and the emission of high harmonics. Moreover, in the expansion (3.5), all terms with
$n$
laser photons and the emission of high harmonics. Moreover, in the expansion (3.5), all terms with
![]() $k>0$
vanish and we again obtain the well-known result that the partial matrix element of the
$k>0$
vanish and we again obtain the well-known result that the partial matrix element of the
![]() $n$
th harmonic contains the Bessel functions
$n$
th harmonic contains the Bessel functions
![]() $\text{J}_{n}$
and
$\text{J}_{n}$
and
![]() $\text{J}_{n\pm 1}$
(Berestetzki et al.
Reference Berestetzki, Lifschitz and Pitajewski1980; Ritus Reference Ritus1985).
$\text{J}_{n\pm 1}$
(Berestetzki et al.
Reference Berestetzki, Lifschitz and Pitajewski1980; Ritus Reference Ritus1985).
It is possible to find a recurrence relation for the ponderomotive integrals:
Subsequent application of this relation helps to reduce the order of the upper index to zero:
Thus, we have to calculate only those ponderomotive integrals with upper index
![]() $k=0$
. Let us now rescale the integration variable in (3.8) as
$k=0$
. Let us now rescale the integration variable in (3.8) as
![]() ${\it\phi}\rightarrow t={\it\phi}/{\rm\Delta}{\it\phi}$
, in order to define the three-parameter master integrals as
${\it\phi}\rightarrow t={\it\phi}/{\rm\Delta}{\it\phi}$
, in order to define the three-parameter master integrals as
as a function of the rescaled variables
It only depends on the shape of the laser pulse and is completely independent of the pulse duration. Note that the master integrals are real valued functions for all symmetric laser pulse shapes.
From stationary phase arguments one can deduce that the master integrals are essentially different from zero only in the regions bounded by the
![]() ${\it\eta}$
-axis and the line
${\it\eta}$
-axis and the line
![]() ${\it\eta}=-{\it\xi}$
. In this region the master integrals are oscillating function for all values of
${\it\eta}=-{\it\xi}$
. In this region the master integrals are oscillating function for all values of
![]() $r$
. This region is visualized as a grey shaded area in figure 2. Outside of this region it rapidly approaches zero.
$r$
. This region is visualized as a grey shaded area in figure 2. Outside of this region it rapidly approaches zero.
Before we continue our discussion of the properties of the master integrals and their pulse shape dependence, let us first represent the partial transition amplitudes
![]() $\mathscr{M}^{(n)}$
in terms of the
$\mathscr{M}^{(n)}$
in terms of the
![]() ${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
by putting together all the expansions:
${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
by putting together all the expansions:
 $$\begin{eqnarray}\displaystyle \mathscr{M}^{(n)} & = & \displaystyle {\rm\Delta}{\it\phi}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}\mathop{\sum }_{k=0}^{\infty }\mathop{\sum }_{{\it\nu}=0}^{k}\frac{(-1)^{{\it\nu}}}{k!}\binom{k}{{\it\nu}}\left(\frac{\ell {\it\alpha}}{2}\right)^{k}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+k-1}(\ell {\it\alpha})\left[\mathscr{T}_{+}-\frac{{\it\alpha}\text{e}^{-\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]{\mathcal{B}}_{n+2{\it\nu}}({\it\xi},{\it\eta})\right.\nonumber\\ \displaystyle & & \displaystyle +\,\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+k+1}(\ell {\it\alpha})\left[\mathscr{T}_{-}-\frac{{\it\alpha}\text{e}^{+\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]{\mathcal{B}}_{n+2+2{\it\nu}}({\it\xi},{\it\eta})\nonumber\\ \displaystyle & & \displaystyle +\left.\,\text{J}_{n+k}(\ell {\it\alpha})[\mathscr{T}_{2}-{\it\beta}\mathscr{T}_{0}]{\mathcal{B}}_{n+2+2{\it\nu}}({\it\xi},{\it\eta})\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{M}^{(n)} & = & \displaystyle {\rm\Delta}{\it\phi}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}\mathop{\sum }_{k=0}^{\infty }\mathop{\sum }_{{\it\nu}=0}^{k}\frac{(-1)^{{\it\nu}}}{k!}\binom{k}{{\it\nu}}\left(\frac{\ell {\it\alpha}}{2}\right)^{k}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+k-1}(\ell {\it\alpha})\left[\mathscr{T}_{+}-\frac{{\it\alpha}\text{e}^{-\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]{\mathcal{B}}_{n+2{\it\nu}}({\it\xi},{\it\eta})\right.\nonumber\\ \displaystyle & & \displaystyle +\,\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+k+1}(\ell {\it\alpha})\left[\mathscr{T}_{-}-\frac{{\it\alpha}\text{e}^{+\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]{\mathcal{B}}_{n+2+2{\it\nu}}({\it\xi},{\it\eta})\nonumber\\ \displaystyle & & \displaystyle +\left.\,\text{J}_{n+k}(\ell {\it\alpha})[\mathscr{T}_{2}-{\it\beta}\mathscr{T}_{0}]{\mathcal{B}}_{n+2+2{\it\nu}}({\it\xi},{\it\eta})\right\}.\end{eqnarray}$$
To obtain the spectrum of nonlinear Compton scattering we have to plug this transition amplitude into (2.12).
For the sake of completeness let us now briefly discuss the partial transition amplitudes in the limit of infinite plane wave laser fields,
![]() $g=1$
. In this case the master integrals turn into
$g=1$
. In this case the master integrals turn into
![]() ${\mathcal{B}}_{r}({\it\xi},{\it\eta})\rightarrow 2{\rm\pi}{\it\delta}({\it\xi}+{\it\eta})$
, i.e. they are localized along the diagonal
${\mathcal{B}}_{r}({\it\xi},{\it\eta})\rightarrow 2{\rm\pi}{\it\delta}({\it\xi}+{\it\eta})$
, i.e. they are localized along the diagonal
![]() ${\it\eta}=-{\it\xi}$
. Moreover, the summation over
${\it\eta}=-{\it\xi}$
. Moreover, the summation over
![]() ${\it\nu}$
yields just a Kronecker delta
${\it\nu}$
yields just a Kronecker delta
![]() ${\it\delta}_{k0}$
such that only the
${\it\delta}_{k0}$
such that only the
![]() $k=0$
term survives in the sum over
$k=0$
term survives in the sum over
![]() $k$
. Therefore we obtain for the transition amplitude for infinite plane waves
$k$
. Therefore we obtain for the transition amplitude for infinite plane waves
 $$\begin{eqnarray}\displaystyle \mathscr{M}^{(n)} & = & \displaystyle 2{\rm\pi}{\it\delta}(\ell -n+\ell {\it\beta}){\rm\Delta}{\it\phi}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}\left\{\text{e}^{\text{i}{\it\varphi}}\text{J}_{n-1}(\ell _{n}{\it\alpha})\left[\mathscr{T}_{+}-\frac{{\it\alpha}\text{e}^{-\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\,\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+1}(\ell _{n}{\it\alpha})\left[\mathscr{T}_{-}-\frac{{\it\alpha}\text{e}^{+\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]+\text{J}_{n}(\ell _{n}{\it\alpha})[\mathscr{T}_{2}-{\it\beta}\mathscr{T}_{0}]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{M}^{(n)} & = & \displaystyle 2{\rm\pi}{\it\delta}(\ell -n+\ell {\it\beta}){\rm\Delta}{\it\phi}(-1)^{n}\text{e}^{-\text{i}n{\it\varphi}}\left\{\text{e}^{\text{i}{\it\varphi}}\text{J}_{n-1}(\ell _{n}{\it\alpha})\left[\mathscr{T}_{+}-\frac{{\it\alpha}\text{e}^{-\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\,\text{e}^{\text{i}{\it\varphi}}\text{J}_{n+1}(\ell _{n}{\it\alpha})\left[\mathscr{T}_{-}-\frac{{\it\alpha}\text{e}^{+\text{i}{\it\phi}}}{2}\mathscr{T}_{0}\right]+\text{J}_{n}(\ell _{n}{\it\alpha})[\mathscr{T}_{2}-{\it\beta}\mathscr{T}_{0}]\right\},\end{eqnarray}$$
with the argument of the Bessel functions now being
![]() $\ell _{n}{\it\alpha}=n{\it\alpha}/(1+{\it\beta})$
, which reproduces the well-known textbook result (Berestetzki et al.
Reference Berestetzki, Lifschitz and Pitajewski1980). The direct comparison between (3.17) and (3.18) impressively demonstrates how much more complex and intricate the case of the pulsed laser fields is, as compared to infinite plane waves. The master integrals
$\ell _{n}{\it\alpha}=n{\it\alpha}/(1+{\it\beta})$
, which reproduces the well-known textbook result (Berestetzki et al.
Reference Berestetzki, Lifschitz and Pitajewski1980). The direct comparison between (3.17) and (3.18) impressively demonstrates how much more complex and intricate the case of the pulsed laser fields is, as compared to infinite plane waves. The master integrals
![]() ${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
, which become trivial in the case of infinite plane waves, cause the increased complexity of the transition amplitude for pulsed plane wave laser fields. They can be considered as a fingerprint of the laser pulse shape.
${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
, which become trivial in the case of infinite plane waves, cause the increased complexity of the transition amplitude for pulsed plane wave laser fields. They can be considered as a fingerprint of the laser pulse shape.
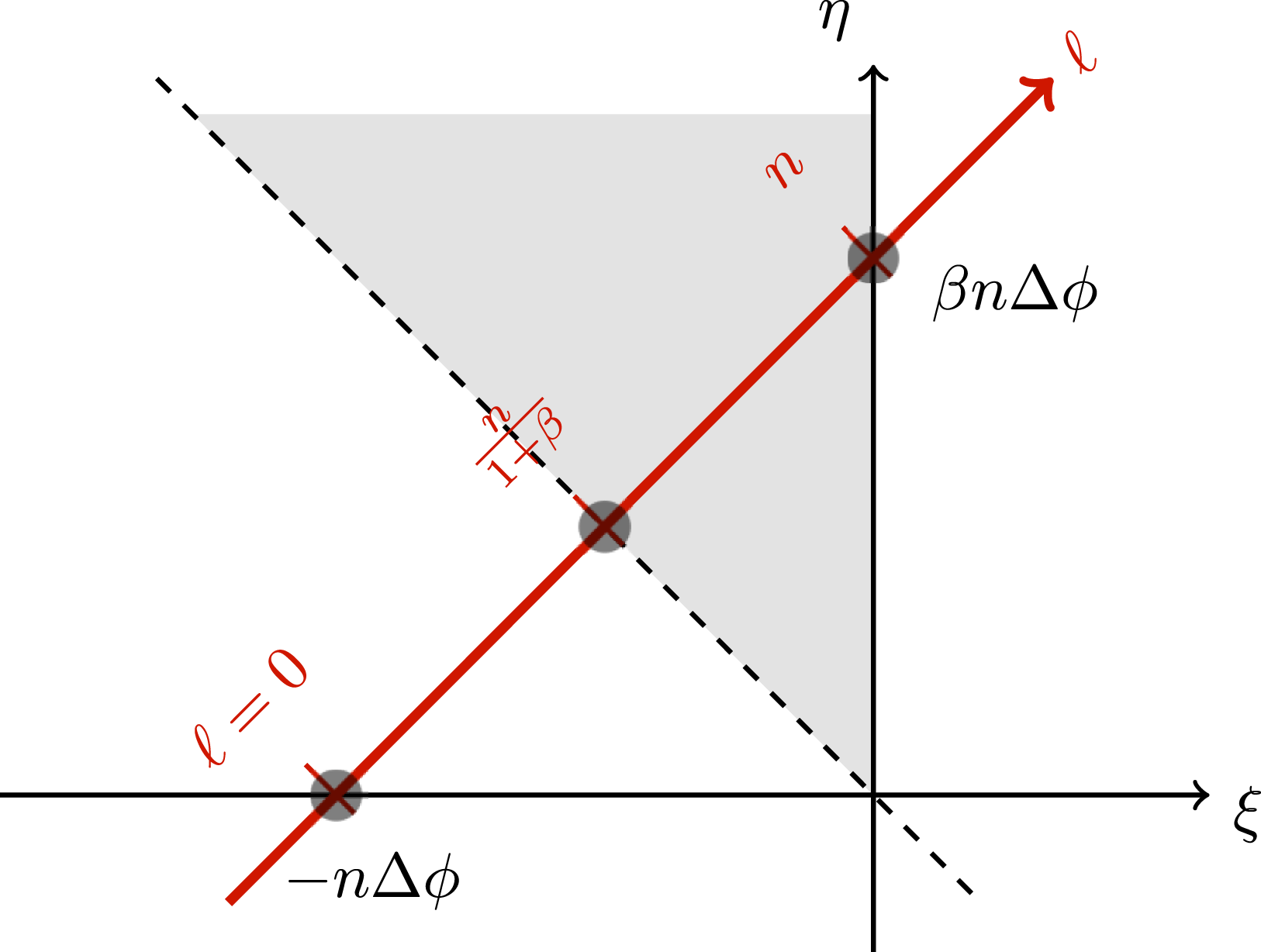
Figure 2. Illustration of how to cut the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane in order to obtain the shape of the spectral lines as a function of
${\it\eta}$
plane in order to obtain the shape of the spectral lines as a function of
![]() $\ell$
for fixed scattering angle
$\ell$
for fixed scattering angle
![]() ${\it\vartheta}$
.
${\it\vartheta}$
.
Let us now return to our discussion of the properties of the master integrals (3.8) by first discussing how the rescaled arguments
![]() ${\it\xi}$
and
${\it\xi}$
and
![]() ${\it\eta}$
relate to the frequency
${\it\eta}$
relate to the frequency
![]() ${\it\omega}^{\prime }$
and scattering angle
${\it\omega}^{\prime }$
and scattering angle
![]() ${\it\vartheta}$
of the emitted photon. In order to obtain the shape of the frequency spectrum as a function of
${\it\vartheta}$
of the emitted photon. In order to obtain the shape of the frequency spectrum as a function of
![]() $\ell$
(or the photon frequency
$\ell$
(or the photon frequency
![]() ${\it\omega}^{\prime }$
by means of (2.9)), one has to cut the functions
${\it\omega}^{\prime }$
by means of (2.9)), one has to cut the functions
![]() ${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
along the straight line
${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
along the straight line
![]() ${\it\eta}={\it\beta}{\it\xi}+n{\it\beta}{\rm\Delta}{\it\phi}$
in the
${\it\eta}={\it\beta}{\it\xi}+n{\it\beta}{\rm\Delta}{\it\phi}$
in the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane, depicted as a red diagonal line in figure 2. This line intersects the
${\it\eta}$
plane, depicted as a red diagonal line in figure 2. This line intersects the
![]() ${\it\xi}$
–axis at
${\it\xi}$
–axis at
![]() ${\it\xi}=-n{\rm\Delta}{\it\phi}$
, the slope is just
${\it\xi}=-n{\rm\Delta}{\it\phi}$
, the slope is just
![]() ${\it\beta}$
(i.e. it depends on the laser intensity), and the intersection with the
${\it\beta}$
(i.e. it depends on the laser intensity), and the intersection with the
![]() ${\it\eta}$
-axis is at
${\it\eta}$
-axis is at
![]() ${\it\eta}={\it\beta}n{\rm\Delta}{\it\phi}$
. Note that the dependence on the scattering angle
${\it\eta}={\it\beta}n{\rm\Delta}{\it\phi}$
. Note that the dependence on the scattering angle
![]() ${\it\vartheta}$
is entirely contained in the parameter
${\it\vartheta}$
is entirely contained in the parameter
![]() ${\it\beta}$
, see (2.11).
${\it\beta}$
, see (2.11).
It is important to note which values of
![]() $\ell$
lie inside the grey shaded area where the master integrals are non-zero: they are exactly those values between the redshifted and unshifted
$\ell$
lie inside the grey shaded area where the master integrals are non-zero: they are exactly those values between the redshifted and unshifted
![]() $n$
th harmonic lines in the infinite plane wave:
$n$
th harmonic lines in the infinite plane wave:
![]() $n/(1+{\it\beta})\leqslant \ell \leqslant n$
, see figure 2. Moreover, we see that the diagonal
$n/(1+{\it\beta})\leqslant \ell \leqslant n$
, see figure 2. Moreover, we see that the diagonal
![]() ${\it\eta}=-{\it\xi}$
represents the redshifted harmonics in the infinite monochromatic plane wave. That means, the region close to the diagonal line
${\it\eta}=-{\it\xi}$
represents the redshifted harmonics in the infinite monochromatic plane wave. That means, the region close to the diagonal line
![]() ${\it\eta}=-{\it\xi}$
is formed close to the centre of the laser pulse where the intensity is largest. In the region close to the
${\it\eta}=-{\it\xi}$
is formed close to the centre of the laser pulse where the intensity is largest. In the region close to the
![]() ${\it\eta}$
-axis the master integrals is formed at the very edges of the laser pulse where the intensity is very low.
${\it\eta}$
-axis the master integrals is formed at the very edges of the laser pulse where the intensity is very low.
Numerical evaluations of the master integral
![]() ${\mathcal{B}}_{1}({\it\xi},{\it\eta})$
are depicted in figure 3 for three different pulse envelopes. We see that each pulse shape generates a distinct pattern of oscillations in the triangular region bounded by the
${\mathcal{B}}_{1}({\it\xi},{\it\eta})$
are depicted in figure 3 for three different pulse envelopes. We see that each pulse shape generates a distinct pattern of oscillations in the triangular region bounded by the
![]() ${\it\eta}$
-axis and the diagonal
${\it\eta}$
-axis and the diagonal
![]() ${\it\eta}=-{\it\xi}$
. For a Gaussian pulse envelope
${\it\eta}=-{\it\xi}$
. For a Gaussian pulse envelope
![]() $g(t)=\text{e}^{-t^{2}/2}$
numerical evaluations of the master integrals are depicted in figure 4 for different values of
$g(t)=\text{e}^{-t^{2}/2}$
numerical evaluations of the master integrals are depicted in figure 4 for different values of
![]() $r$
. One can see that the larger the value of
$r$
. One can see that the larger the value of
![]() $r$
the stronger the function is localized close to the line
$r$
the stronger the function is localized close to the line
![]() ${\it\eta}=-{\it\xi}$
(i.e. the nonlinear Compton edge in the limit of infinite plane waves). By recalling how we need to cut the
${\it\eta}=-{\it\xi}$
(i.e. the nonlinear Compton edge in the limit of infinite plane waves). By recalling how we need to cut the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane to obtain the frequency spectrum we easily deduce that for longer pulses or higher harmonics the spectral lines contain more oscillations. This observation is in line with results using the saddle point method (Seipt & Kämpfer Reference Seipt and Kämpfer2013b
).
${\it\eta}$
plane to obtain the frequency spectrum we easily deduce that for longer pulses or higher harmonics the spectral lines contain more oscillations. This observation is in line with results using the saddle point method (Seipt & Kämpfer Reference Seipt and Kämpfer2013b
).

Figure 3. Numerical evaluation of the master integral
![]() ${\mathcal{B}}_{1}({\it\xi},{\it\eta})$
for different pulse shapes: a Gaussian
${\mathcal{B}}_{1}({\it\xi},{\it\eta})$
for different pulse shapes: a Gaussian
![]() $g(t)=\text{e}^{-t^{2}/2}$
(a), an exponential
$g(t)=\text{e}^{-t^{2}/2}$
(a), an exponential
![]() $g=\text{e}^{-|t|}$
(b), and a supergaussian
$g=\text{e}^{-|t|}$
(b), and a supergaussian
![]() $g=\text{e}^{-t^{4}/2}$
(c).
$g=\text{e}^{-t^{4}/2}$
(c).

Figure 4. Numerical evaluation of the master integral (3.16) for a Gaussian pulse envelope
![]() $g=\text{e}^{-t^{2}/2}$
in the
$g=\text{e}^{-t^{2}/2}$
in the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane for increasing values of
${\it\eta}$
plane for increasing values of
![]() $r$
from (a–c).
$r$
from (a–c).
Before we conclude this paragraph, let us explicitly state how the rather abstract variables
![]() ${\it\xi}$
and
${\it\xi}$
and
![]() ${\it\eta}$
are related to the physically observable photon frequency
${\it\eta}$
are related to the physically observable photon frequency
![]() ${\it\omega}^{\prime }$
and scattering angle
${\it\omega}^{\prime }$
and scattering angle
![]() ${\it\vartheta}$
. Those expressions explicitly read
${\it\vartheta}$
. Those expressions explicitly read
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\omega}^{\prime }({\it\xi},{\it\eta})=\frac{{\it\xi}+n{\rm\Delta}{\it\phi}}{{\rm\Delta}{\it\phi}+\displaystyle \frac{4{\it\omega}}{ma_{0}^{2}}{\it\eta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\omega}^{\prime }({\it\xi},{\it\eta})=\frac{{\it\xi}+n{\rm\Delta}{\it\phi}}{{\rm\Delta}{\it\phi}+\displaystyle \frac{4{\it\omega}}{ma_{0}^{2}}{\it\eta}}, & \displaystyle\end{eqnarray}$$
By inspecting figure 2 together (2.11) we find that for any harmonic
![]() $n$
and any value of
$n$
and any value of
![]() $r$
, the physically relevant part of the master integral is located in a triangular region with the corner points
$r$
, the physically relevant part of the master integral is located in a triangular region with the corner points
![]() $({\it\xi},{\it\eta})=(0,0)$
,
$({\it\xi},{\it\eta})=(0,0)$
,
![]() $(0,n{\rm\Delta}{\it\phi}a_{0}^{2}/2)$
and
$(0,n{\rm\Delta}{\it\phi}a_{0}^{2}/2)$
and
![]() $({\it\xi}_{0},-{\it\xi}_{0})$
with
$({\it\xi}_{0},-{\it\xi}_{0})$
with
![]() ${\it\xi}_{0}=n{\rm\Delta}{\it\phi}a_{0}^{2}/(2+a_{0}^{2})$
. That means for different
${\it\xi}_{0}=n{\rm\Delta}{\it\phi}a_{0}^{2}/(2+a_{0}^{2})$
. That means for different
![]() $n$
, pulse duration
$n$
, pulse duration
![]() ${\rm\Delta}{\it\phi}$
and
${\rm\Delta}{\it\phi}$
and
![]() $a_{0}$
different parts of the
$a_{0}$
different parts of the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane describe the spectrum of backscattered photons. The boundaries of these triangular regions are marked in figure 5(a) for two different sets of parameters. When these areas are transformed to
${\it\eta}$
plane describe the spectrum of backscattered photons. The boundaries of these triangular regions are marked in figure 5(a) for two different sets of parameters. When these areas are transformed to
![]() ${\it\omega}^{\prime }$
and
${\it\omega}^{\prime }$
and
![]() ${\it\vartheta}$
we obtain the distributions in figure 5(b) and (c), respectively. They strongly resemble the spectral line shapes in the incident electron rest frame found previously, e.g. in (Seipt & Kämpfer Reference Seipt and Kämpfer2013b
).
${\it\vartheta}$
we obtain the distributions in figure 5(b) and (c), respectively. They strongly resemble the spectral line shapes in the incident electron rest frame found previously, e.g. in (Seipt & Kämpfer Reference Seipt and Kämpfer2013b
).
For the sake of completeness, we also provide here the corresponding transformation relations in the laboratory frame where the electron counterpropagates the laser pulse with a Lorentz factor
![]() ${\it\gamma}$
:
${\it\gamma}$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\omega}_{lab}^{\prime }({\it\xi},{\it\eta})=\frac{{\it\omega}{\it\gamma}^{2}(1+v)^{2}({\it\xi}+n{\rm\Delta}{\it\phi})}{\displaystyle \frac{1+v}{1-v+v\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}}\left({\rm\Delta}{\it\phi}+\frac{4}{a_{0}^{2}}\frac{{\it\omega}{\it\gamma}(1+v){\it\eta}}{m}\right)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\omega}_{lab}^{\prime }({\it\xi},{\it\eta})=\frac{{\it\omega}{\it\gamma}^{2}(1+v)^{2}({\it\xi}+n{\rm\Delta}{\it\phi})}{\displaystyle \frac{1+v}{1-v+v\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}}\left({\rm\Delta}{\it\phi}+\frac{4}{a_{0}^{2}}\frac{{\it\omega}{\it\gamma}(1+v){\it\eta}}{m}\right)}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\vartheta}_{lab}({\it\xi},{\it\eta})=\arccos \left(\frac{\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}-1+v}{1-v+v\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\vartheta}_{lab}({\it\xi},{\it\eta})=\arccos \left(\frac{\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}-1+v}{1-v+v\displaystyle \frac{4}{a_{0}^{2}}\frac{{\it\eta}}{{\it\xi}+n{\rm\Delta}{\it\phi}}}\right), & \displaystyle\end{eqnarray}$$

Figure 5. Transformation of the triangular regions in the
![]() ${\it\xi}$
–
${\it\xi}$
–
![]() ${\it\eta}$
plane to the variables
${\it\eta}$
plane to the variables
![]() ${\it\omega}^{\prime }$
and
${\it\omega}^{\prime }$
and
![]() ${\it\vartheta}$
. The solid, dashed and dash-dotted curves correspond to each other.
${\it\vartheta}$
. The solid, dashed and dash-dotted curves correspond to each other.

Figure 6. Differential on-axis photon emission probability in the laboratory frame for
![]() $a_{0}=1.5$
,
$a_{0}=1.5$
,
![]() ${\rm\Delta}{\it\phi}=25$
, a Gaussian pulse shape and
${\rm\Delta}{\it\phi}=25$
, a Gaussian pulse shape and
![]() ${\it\gamma}=100$
. The direct numerical evaluation of the dynamic integrals (blue solid) coincides perfectly with the evaluations of the master integrals (red dashed).
${\it\gamma}=100$
. The direct numerical evaluation of the dynamic integrals (blue solid) coincides perfectly with the evaluations of the master integrals (red dashed).
3.3 Universal behaviour of high-order harmonics
Let us now draw some conclusions about the shape of very high-order harmonics. One can notice that for large values of
![]() $r$
, the powers of
$r$
, the powers of
![]() $g^{r}(t)$
become strongly localized around
$g^{r}(t)$
become strongly localized around
![]() $t\approx 0$
. Thus, the main contribution to the master integral, (3.16), is provided by the region of
$t\approx 0$
. Thus, the main contribution to the master integral, (3.16), is provided by the region of
![]() $g(t)$
around the maximum at
$g(t)$
around the maximum at
![]() $t=0$
. For sufficiently smooth pulse envelopesFootnote
1
$t=0$
. For sufficiently smooth pulse envelopesFootnote
1
![]() $g(t)$
a Taylor expansion around the point
$g(t)$
a Taylor expansion around the point
![]() $t=0$
reads
$t=0$
reads
Defining
![]() ${\it\tau}^{2}=1/|g^{\prime \prime }(0)|$
and employing the known limit
${\it\tau}^{2}=1/|g^{\prime \prime }(0)|$
and employing the known limit
![]() $(1+x/r)^{r}\stackrel{r\rightarrow \infty }{\rightarrow }\text{e}^{x}$
, we find
$(1+x/r)^{r}\stackrel{r\rightarrow \infty }{\rightarrow }\text{e}^{x}$
, we find
which is of Gaussian shape and does not depend on any details of the primary pulse shape, except for the curvature at the maximum, i.e. the second derivative
![]() $g^{\prime \prime }(0)$
at
$g^{\prime \prime }(0)$
at
![]() $t=0$
. Note that if one is concerned about laser pulses with a flat top envelope (in the sense that
$t=0$
. Note that if one is concerned about laser pulses with a flat top envelope (in the sense that
![]() $g^{\prime \prime }(0)=0$
), the Taylor series in (3.23) can be extended further, and will eventually lead to a supergaussian shape of
$g^{\prime \prime }(0)=0$
), the Taylor series in (3.23) can be extended further, and will eventually lead to a supergaussian shape of
![]() $g^{r}(t)$
.
$g^{r}(t)$
.
The conclusion is that for sufficiently high harmonic order the master integral is approximately given by
Because for large values of
![]() $r$
the main contributions to this integral come from a narrow region around
$r$
the main contributions to this integral come from a narrow region around
![]() $t=0$
, we can approximate
$t=0$
, we can approximate
![]() $\int \text{d}tg^{2}(t)$
polynomially around
$\int \text{d}tg^{2}(t)$
polynomially around
![]() $t=0$
up to the third order. This allows us to give an analytic expression for the master integrals
$t=0$
up to the third order. This allows us to give an analytic expression for the master integrals
![]() ${\mathcal{B}}_{r}$
for large values of
${\mathcal{B}}_{r}$
for large values of
![]() $r\rightarrow \infty$
as
$r\rightarrow \infty$
as
in terms of the Airy function Ai (Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953). The central conclusion here is that for very large values of
![]() $r$
the shape of the harmonic lines approximate the shape of the harmonics for a Gaussian laser pulse with temporal duration
$r$
the shape of the harmonic lines approximate the shape of the harmonics for a Gaussian laser pulse with temporal duration
![]() ${\it\tau}/\sqrt{r}=1/\sqrt{r|g^{\prime \prime }(0)|}$
. The only specific input from the original pulse shape
${\it\tau}/\sqrt{r}=1/\sqrt{r|g^{\prime \prime }(0)|}$
. The only specific input from the original pulse shape
![]() $g$
that affects the shape of the high harmonic spectral lines is the curvature of the pulse envelope at the maximum.
$g$
that affects the shape of the high harmonic spectral lines is the curvature of the pulse envelope at the maximum.
3.4 Explicit closed form analytic results for the master integrals
We finally provide explicit closed form analytic expressions for the master integrals
![]() ${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
for several different laser pulse shapes
${\mathcal{B}}_{r}({\it\xi},{\it\eta})$
for several different laser pulse shapes
![]() $g$
.
$g$
.
3.4.1 Hyperbolic secant pulse shape
For a hyperbolic secant pulse,
![]() $g(t)=1/\cosh (t)$
, we have
$g(t)=1/\cosh (t)$
, we have
![]() $\int g^{2}\text{d}t=\tanh t$
, and the master integral
$\int g^{2}\text{d}t=\tanh t$
, and the master integral
can be evaluated by transforming the integration variable according to
![]() $z=1/(2\text{e}^{t}\cosh t)$
, yielding
$z=1/(2\text{e}^{t}\cosh t)$
, yielding
This integral can be evaluated as
with the Gamma function
![]() ${\it\Gamma}(z)$
and the confluent hyperbolic function
${\it\Gamma}(z)$
and the confluent hyperbolic function
![]() $_{1}F_{1}(a,b;z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953). An equivalent representation of (3.29) can be given in terms of the generalized Laguerre functions
$_{1}F_{1}(a,b;z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953). An equivalent representation of (3.29) can be given in terms of the generalized Laguerre functions
![]() ${\mathcal{L}}_{{\it\nu}}^{{\it\lambda}}(z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953) as
${\mathcal{L}}_{{\it\nu}}^{{\it\lambda}}(z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953) as
 $$\begin{eqnarray}\displaystyle {\mathcal{B}}_{r}({\it\xi},{\it\eta})=\frac{2^{r-1}\text{e}^{-\text{i}{\it\eta}}{\rm\pi}}{\sin \displaystyle \left(\frac{{\rm\pi}}{2}(r+\text{i}{\it\xi})\right)}{\mathcal{L}}_{-(r+\text{i}{\it\xi})/2}^{r-1}(2\text{i}{\it\eta}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}_{r}({\it\xi},{\it\eta})=\frac{2^{r-1}\text{e}^{-\text{i}{\it\eta}}{\rm\pi}}{\sin \displaystyle \left(\frac{{\rm\pi}}{2}(r+\text{i}{\it\xi})\right)}{\mathcal{L}}_{-(r+\text{i}{\it\xi})/2}^{r-1}(2\text{i}{\it\eta}). & & \displaystyle\end{eqnarray}$$
3.4.2 Exponential pulse shape
For a pulse shape of the form
![]() $g(t)=\text{e}^{-|t|}$
the master integral takes the form
$g(t)=\text{e}^{-|t|}$
the master integral takes the form
After a substitution
![]() $z=((\text{i}{\it\eta})/2)\text{e}^{-2t}$
we obtain
$z=((\text{i}{\it\eta})/2)\text{e}^{-2t}$
we obtain
which can be expressed as
with the lower incomplete gamma function
![]() ${\it\gamma}(a,z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953),
${\it\gamma}(a,z)$
(Erdélyi et al.
Reference Erdélyi, Magnus, Oberhettinger and Tricomi1953),
3.4.3 Staircase pulse shapes
Let us assume the pulse envelope is staircase, defined as
![]() $g(t)=\sum _{k=1}^{N}{\it\nu}_{k}{\it\chi}_{I_{k}}(t)$
for
$g(t)=\sum _{k=1}^{N}{\it\nu}_{k}{\it\chi}_{I_{k}}(t)$
for
![]() $t>0$
, with
$t>0$
, with
![]() ${\it\nu}_{k}$
being the height of the
${\it\nu}_{k}$
being the height of the
![]() $k$
th step (as measured from the ground level) and the characteristic function
$k$
th step (as measured from the ground level) and the characteristic function
![]() ${\it\chi}_{I_{k}}(t)=1$
if
${\it\chi}_{I_{k}}(t)=1$
if
![]() $t\in I_{k}=[(k-1)/N,k/N)$
, and zero otherwise. (For
$t\in I_{k}=[(k-1)/N,k/N)$
, and zero otherwise. (For
![]() $t<0$
the envelope is fully defined by the symmetry
$t<0$
the envelope is fully defined by the symmetry
![]() $g(-t)=g(t)$
.) For the moment we assume that the step height increases uniformly,
$g(-t)=g(t)$
.) For the moment we assume that the step height increases uniformly,
![]() ${\it\nu}_{k}=(N-k+1)/N$
, but a generalization to arbitrary steps is obvious. A compelling feature of the staircase pulse is the possibility to approximate many different smooth pulse shapes in the limit of infinite steps
${\it\nu}_{k}=(N-k+1)/N$
, but a generalization to arbitrary steps is obvious. A compelling feature of the staircase pulse is the possibility to approximate many different smooth pulse shapes in the limit of infinite steps
![]() $N\rightarrow \infty$
, just by adjusting the step heights. For instance, the uniform staircase discussed here would converge to a smooth triangle pulse.
$N\rightarrow \infty$
, just by adjusting the step heights. For instance, the uniform staircase discussed here would converge to a smooth triangle pulse.
By splitting the
![]() $t$
-integration range into the intervals
$t$
-integration range into the intervals
![]() $I_{k}$
where
$I_{k}$
where
![]() $g$
is constant we evaluate the master integral as
$g$
is constant we evaluate the master integral as
 $$\begin{eqnarray}\displaystyle {\mathcal{B}}_{r}({\it\xi},{\it\eta})=\mathop{\sum }_{k=1}^{N}2({\it\nu}_{k})^{r}\frac{\sin \displaystyle \frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}}{\displaystyle \frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}}\cos \left({\it\eta}{\it\Phi}_{k}+\frac{2k-1}{N}\frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}_{r}({\it\xi},{\it\eta})=\mathop{\sum }_{k=1}^{N}2({\it\nu}_{k})^{r}\frac{\sin \displaystyle \frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}}{\displaystyle \frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}}\cos \left({\it\eta}{\it\Phi}_{k}+\frac{2k-1}{N}\frac{{\it\xi}+{\it\eta}{\it\nu}_{k}^{2}}{2}\right), & & \displaystyle\end{eqnarray}$$
with
For
![]() $N=1$
we recover the well-known result of a sinc profile for the box pulse which is aligned along the
$N=1$
we recover the well-known result of a sinc profile for the box pulse which is aligned along the
![]() ${\it\eta}=-{\it\xi}$
diagonal, i.e. it corresponds to the usual infinite plane wave redshift. While the bandwidth of the laser pulse translates to the Compton scattered light, we see no indication of the ponderomotive broadening due to a gradual ramp up of the laser intensity. How this ponderomotive broadening effect develops can be seen quite instructively when going to a pulse with more than one step. For
${\it\eta}=-{\it\xi}$
diagonal, i.e. it corresponds to the usual infinite plane wave redshift. While the bandwidth of the laser pulse translates to the Compton scattered light, we see no indication of the ponderomotive broadening due to a gradual ramp up of the laser intensity. How this ponderomotive broadening effect develops can be seen quite instructively when going to a pulse with more than one step. For
![]() $N$
steps we observe a total of
$N$
steps we observe a total of
![]() $N$
strips in the
$N$
strips in the
![]() ${\it\eta}$
–
${\it\eta}$
–
![]() ${\it\xi}$
plane that are centred along the lines
${\it\xi}$
plane that are centred along the lines
![]() ${\it\eta}=-{\it\xi}/{\it\nu}_{k}^{2}$
. On each of the steps the radiation is emitted with their respective redshift, determined by the square of the
${\it\eta}=-{\it\xi}/{\it\nu}_{k}^{2}$
. On each of the steps the radiation is emitted with their respective redshift, determined by the square of the
![]() $k$
th step height as
$k$
th step height as
![]() $\ell =n/(1+{\it\beta}{\it\nu}_{k}^{2})$
. With increasing
$\ell =n/(1+{\it\beta}{\it\nu}_{k}^{2})$
. With increasing
![]() $N$
these strips eventually are overlapping, reproducing the typical picture from the smooth pulses discussed before. Thus, the staircase pulse model discussed here helps to investigate the transition from the case of a constant amplitude laser pulse to the case of smooth pulses where the ponderomotive broadening sets in and strongly influences the nonlinear Compton spectrum.
$N$
these strips eventually are overlapping, reproducing the typical picture from the smooth pulses discussed before. Thus, the staircase pulse model discussed here helps to investigate the transition from the case of a constant amplitude laser pulse to the case of smooth pulses where the ponderomotive broadening sets in and strongly influences the nonlinear Compton spectrum.
4 Conclusions
In summary, we provided in this paper a comprehensive and completely analytical evaluation of the nonlinear Compton transition amplitude. It was found that the dependence on the shape of the strong laser pulse can be traced back to a class of three-parameter master integrals. In addition, all the dependence on the pulse duration can be conveniently scaled out from the master integral. For certain shapes of the laser pulse envelope we provided explicit analytical expressions for the master integrals. In addition, for very high harmonics we find a universal behaviour of the shape of the harmonic lines.
In this paper we studied only the case of circularly polarized laser light. The laser polarization affects the form of the Jacobi–Anger type expansion (3.2) and the subsequent extraction of the laser pulse envelope from the argument of the Bessel functions via (3.5). In the case of an elliptic or linear laser polarization we would encounter generalized two-argument Bessel functions (Korsch, Klumpp & Witthaut Reference Korsch, Klumpp and Witthaut2006; Seipt Reference Seipt2012). But eventually the laser pulse shape dependence is described by exactly the same master integrals (3.8) as for circular laser polarization discussed in this paper.
We would like to stress that the analytical structure of the strong field
![]() $\unicode[STIX]{x1D64E}$
matrix is similar also for other first-order strong-field QED processes such as Breit–Wheeler pair production, or pair annihilation. Thus, our analytic results could be easily translated to these processes too.
$\unicode[STIX]{x1D64E}$
matrix is similar also for other first-order strong-field QED processes such as Breit–Wheeler pair production, or pair annihilation. Thus, our analytic results could be easily translated to these processes too.
Acknowledgements
This work was supported in part by the Helmholtz Association (Helmholtz Young Investigators group VH-NG-1037).









