Published online by Cambridge University Press: 05 November 2019
Beam-driven instabilities are considered in a pulsar plasma assuming that both the background plasma and the beam are relativistic Jüttner distributions. In the rest frame of the background, the only waves that can satisfy the resonance condition are in a tiny range of slightly subluminal phase speeds. The growth rate for the kinetic (or maser) version of the weak-beam instability is much smaller than has been estimated for a relativistically streaming Gaussian distribution, and the reasons for this are discussed. The growth rate for the reactive version of the weak-beam instability is treated in a conventional way. We compare the results with exact calculations, and find that the approximate solutions are not consistent with the exact results. We conclude that, for plausible parameters, there is no reactive version of the instability. The growth rate in the pulsar frame is smaller than that in the rest frame of the background plasma by a factor 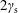 $2\unicode[STIX]{x1D6FE}_{\text{s}}$, where
$2\unicode[STIX]{x1D6FE}_{\text{s}}$, where 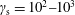 $\unicode[STIX]{x1D6FE}_{\text{s}}=10^{2}{-}10^{3}$ is the Lorentz factor of the bulk motion of the background plasma, placing a further constraint on effective wave growth. Based on these results, we argue that beam-driven wave growth probably plays no role in pulsar radio emission.
$\unicode[STIX]{x1D6FE}_{\text{s}}=10^{2}{-}10^{3}$ is the Lorentz factor of the bulk motion of the background plasma, placing a further constraint on effective wave growth. Based on these results, we argue that beam-driven wave growth probably plays no role in pulsar radio emission.