Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T00:42:01.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave dispersion in pulsar plasma. Part 2. Pulsar frame

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  26 June 2019

M. Z. Rafat Open the ORCID record for M. Z. Rafat [Opens in a new window] ,
D. B. Melrose Open the ORCID record for D. B. Melrose [Opens in a new window]  and
A. Mastrano Open the ORCID record for A. Mastrano [Opens in a new window]
M. Z. Rafat
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
D. B. Melrose*
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
A. Mastrano
Affiliation:
SIfA, School of Physics, The University of Sydney, NSW 2006, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wave dispersion in a pulsar plasma is discussed emphasizing the relevance of different inertial frames, notably the plasma rest frame 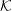${\mathcal{K}}$ and the pulsar frame 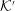${\mathcal{K}}^{\prime }$ in which the plasma is streaming with speed 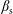$\unicode[STIX]{x1D6FD}_{\text{s}}$. The effect of a Lorentz transformation on both subluminal, 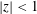$|z|<1$, and superluminal, 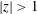$|z|>1$, waves is discussed. It is argued that the preferred choice for a relativistically streaming distribution should be a Lorentz-transformed Jüttner distribution; such a distribution is compared with other choices including a relativistically streaming Gaussian distribution. A Lorentz transformation of the dielectric tensor is written down, and used to derive an explicit relation between the relativistic plasma dispersion functions in 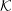${\mathcal{K}}$ and 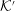${\mathcal{K}}^{\prime }$. It is shown that the dispersion equation can be written in an invariant form, implying a one-to-one correspondence between wave modes in any two inertial frames. Although there are only three modes in the plasma rest frame, it is possible for backward-propagating or negative-frequency solutions in 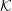${\mathcal{K}}$ to transform into additional forward-propagating, positive-frequency solutions in 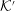${\mathcal{K}}^{\prime }$ that may be regarded as additional modes.

Keywords

astrophysical plasmasplasma instabilitiesplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 3 , June 2019 , 905850311
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arons, J. & Barnard, J. J. 1986 Wave propagation in pulsar magnetospheres – dispersion relations and normal modes of plasmas in superstrong magnetic fields. Astrophys. J. 302, 120–137.Google Scholar
Asseo, E. & Melikidze, G. I. 1998 Non-stationary pair plasma in a pulsar magnetosphere and the two-stream Instability. Mon. Not. R. Astron. Soc. 301, 59–71.Google Scholar
Beskin, V. S., Gurevich, A. V. & Istomin, Y. N. 1993 Physics of the Pulsar Magnetosphere. Cambridge University Press.Google Scholar
Cairns, I. H., Li, B. & Schmidt, J. M. 2017 Chapter 14 – importance of kappa distributions to solar radio bursts. In Kappa Distributions (ed. Livadiotis, G.), pp. 549–567. Elsevier.Google Scholar
Cordes, J. M. 1978 Observational limits on the location of pulsar emission regions. Astrophys. J. 222, 1006–1011.Google Scholar
Gedalin, M., Melrose, D. B. & Gruman, E. 1998 Long waves in a relativistic pair plasma in a strong magnetic field. Phys. Rev. E 57, 3399–3410.Google Scholar
Gupta, Y. & Gangadhara, R. T. 2003 Understanding the radio emission geometry of multiple-component radio pulsars from retardation and aberration effects. Astrophys. J. 584, 418–426.Google Scholar
Istomin, Y. 2001 Propagation of electromagnetic waves in pulsar magnetospheres. Astrophys. Space Sci. 278, 77–80.Google Scholar
Kaplan, S. A. & Tsytovich, V. N. 1973 Plasma Astrophysics. Pergamon Press.Google Scholar
Lazar, M., Stockem, A. & Schlickeiser, R. 2010 Towards a relativistically correct characterization of counterstreaming plasmas. I. Distribution functions. Open Plasma Phys. J. 3, 138–147.Google Scholar
Lesch, H., Jessner, A., Kramer, M. & Kunzl, T. 1998 On the possibility of curvature radiation from radio pulsars. Astron. Astrophys. 332, L21–L24.Google Scholar
Lominadze, J. G. & Pataraya, A. D. 1982 Some nonlinear mechanisms of pulsar emission. Phys. Scr. T2, 215–222.Google Scholar
Lyne, A. G. & Graham-Smith, F. 2006 Pulsar Astronomy. Cambridge University Press.Google Scholar
Melrose, D. B. 1973 A covariant formulation of wave dispersion. Plasma Phys. 15, 99–106.Google Scholar
Melrose, D. B. 2008 Quantum Plasmadynamics: Unmagnetized Plasmas. Springer.Google Scholar
Melrose, D. B. 2013 Quantum Plasmadynamics: Magnetized Plasmas. Springer.Google Scholar
Melrose, D. B. & Gedalin, M. E. 1999 Relativistic plasma emission and pulsar radio emission: a critique. Astrophys. J. 521, 351–361.Google Scholar
Rafat, M. Z., Melrose, D. B. & Mastrano, A. 2019a Wave dispersion in pulsar plasma. Part 1. Plasma rest frame. J. Plasma Phys. 85, 905850305.Google Scholar
Rafat, M. Z., Melrose, D. B. & Mastrano, A. 2019b Wave dispersion in pulsar plasma. Part 3. Beam-driven instabilities. J. Plasma Phys. (submitted).Google Scholar