Published online by Cambridge University Press: 13 March 2009
Transverse instabilities in an electron gas with a neutralizing background, in the absence of a permanent magnetic field are discussed, mostly when the equilibrium velocity distribution is slightly spheroidal, i.e. of the form
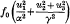
with α ˜ γ and with the functional form of f0 not given explicitly. It is found that two types of unstable waves exist; one grows at a rate proportional to ε½‖ cos θ‖3 whenever ε > 0, the other at a rate proportional to(ε cos2θ)½ whenever ε cos 2θ > 0, where ε = (γ2/α2) — 1, and θ is the angle the wave vector makes with the axis of symmetry of the velocity spheroid. It is shown that within the approximation we are working the complex phase velocity is pure imaginary, i.e. the unstable waves are standing waves. The effect of a small permanent magnetic field is considered. The phase velocity becomes complex, at least for propagation parallel to the magnetic field and the instability rate decreases by a factor 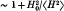 where H0 is the permanent magnetic field and 〈H2〉½ the r.m.s. maximum field that grows before non-linear effects take over. The maximum instability rate is compared with the collision rate and is found to be higher in low density, high temperature plasmas such as the solar wind. An application to collisionless shock theory is suggested.
where H0 is the permanent magnetic field and 〈H2〉½ the r.m.s. maximum field that grows before non-linear effects take over. The maximum instability rate is compared with the collision rate and is found to be higher in low density, high temperature plasmas such as the solar wind. An application to collisionless shock theory is suggested.