The electrostatic modes for which k is perpendicular to the impressed field B0 (the ‘Bernstein modes’) have been examined, and dispersion curves (w vs. k) have been calculated numerically for hybrid frequencies in the vicinity of the thirtieth to fortieth harmonic of the gyrofrequency. 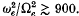Although the calculations were performed for the lower hybrid case (ion branch), they also apply to the upper hybrid cases in which the plasma parameter The structure of the dispersion curves for these large values of plasma parameter differs from that for smaller values 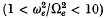investigated by others, in that broad bands in wave-number space have very small group speeds in narrow frequency bands close to many of the gyrofrequency harmonics. All of the Bernstein modes examined have group speeds less than 37 % of the ion thermal speed, and can be classified as very slow waves. Furthermore, the spectrum of propagating Bernstein modes is broadened as 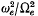becomes large, with an effective total transmission region from the gyrofrequency up to several harmonics of gyrofrequency above the hybrid frequency.