Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T11:06:01.300Z Has data issue: false hasContentIssue false
  • English
  • Français

The stochastic tetrad magneto-hydrodynamics via functional formalism

Part of: Complex Plasma Phenomena

Published online by Cambridge University Press:  02 October 2015

Massimo Materassi  and
Giuseppe Consolini
Massimo Materassi*
Affiliation:
Istituto dei Sistemi Complessi, CNR, via Madonna del Piano 10, Sesto Fiorentino (Fi), Italy
Giuseppe Consolini
Affiliation:
INAF-Istituto di Astrofisica e Planetologia Spaziali, via del Fosso del Cavaliere 100, 00133 Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we discuss an application of the Tetrad Dynamics approach, a stochastic dynamical theory already introduced in hydrodynamic turbulence, to incompressible magneto-hydrodynamics. This theoretical framework is capable of taking into account some crucial aspects of turbulent plasmas, namely, (i) its material nature, which is stressed through the adoption of Lagrangian variables, (ii) its probabilistic dynamics, which is fundamental to understand the intermittency and highly irregular nature of turbulence, and (iii) the multi-scale character of interactions, which is approached by promoting the space size of parcels to the role of a dynamical variable. In particular, here, we construct the probabilistic equations of motion for quantities describing the evolution of a turbulent plasma (a matrix 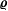${\bf\varrho}$ describing the parcel’s shape, the plasma velocity and magnetic field coarse-grained gradient tensors, $\unicode[STIX]{x1D648}$ and 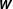$\unicode[STIX]{x1D652}$), resorting the functional formalism of classical statistical dynamics. Through the introduction of a stochastic action and using a path integral approach, the statistical properties of 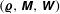$({\bf\varrho},\unicode[STIX]{x1D648},\unicode[STIX]{x1D652})$ can be derived from those of noises appearing in their equations of motion, both at equilibrium and out of equilibrium.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 6 , December 2015 , 495810602
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bennett, A. F. 2006 Lagrangian Fluid Dynamics. Monographs on Mechanics. Cambridge University Press.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.CrossRefGoogle Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4, 782–793.CrossRefGoogle Scholar
Celani, A., Mazzino, A. & Pumir, A. 2003 Turbulence and stochastic processes. Lect. Notes Phys. 636, 173–186.Google Scholar
Chang, T. 1999 Self-organized criticality, multifractal spectra, and intermittent merging of coherent structures in the magnetotail. Astrophys. Space Sci. 264, 303–316.CrossRefGoogle Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11, 2394–2410.Google Scholar
Consolini, G., Materassi, M., Marcucci, M. F. & Pallocchia, G. 2015 Statistics of velocity gradient tensor in space plasma turbulent flows. Astrophys. J. (in press).CrossRefGoogle Scholar
Dallas, V. & Alexakis, A. 2013 Structures and dynamics of small scales in decaying magnetohydrodynamic turbulence. Phys. Fluids 25, 105106.CrossRefGoogle Scholar
Feynman, R. P. & Hibbs, A. R. 1965 Quantum Mechanics and Path Integrals. McGraw-Hill.Google Scholar
Frisch, U. 1995 Turbulence, the Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Gibbon, J. D. & Holm, D. D. 2007 Lagrangian particle paths and ortho-normal quaternion frames. Nonlinearity 20, 1745–1759.Google Scholar
Haken, H. 1983 Synergetics, an Introduction. Springer.Google Scholar
Kallenrode, M.-B. 2004 Space Physics: An Introduction to Plasmas and Particles in the Heliosphere and Magnetospheres, Advanced Texts in Physics. Springer.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1980 The Classical Theory of Fields, Course of Theoretical Physics, vol. 2. Butterworth-Heinman.Google Scholar
Martin, P. C., Siggia, E. D. & Rose, H. A. 1973 Statistical dynamics of classical systems. Phys. Rev. A 8, 423–437.Google Scholar
Materassi, M. 2014 Lagrangian hydrodynamimagnetic turbulence in the plasma sheetcs, entropy and dissipation. In Hydrodynamics (ed. Schulz, H. E.), InTech Publication. Google Scholar
Materassi, M. 2015 Metriplectic algebra for dissipative fluids in lagrangian formulation. Entropy 17, 1329–1346; MDPI AG, Basel, Switzerland.CrossRefGoogle Scholar
Materassi, M. & Consolini, G. 2008 Turning the resistive MHD into a stochastic field theory. Nonlinear Process. Geophys. 15, 701–709.Google Scholar
Materassi, M., Consolini, G., Smith, N. & De Marco, R. 2012 Information theory analysis of cascading process in a synthetic model of fluid turbulence. Entropy 16, 1272–1286.Google Scholar
Materassi, M., Consolini, G. & Tassi, E. 2012 Sub-fluid models in dissipative magneto-hydrodynamics. In Topics in Magnetohydrodynamics (ed. Linjin, Z.), InTech Pub. Google Scholar
Matthaeus, W. H. & Goldstein, M. L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028.Google Scholar
Müller, W.-C. & Biskamp, D. 2000 Scaling properties of three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 84, 475.Google Scholar
Phythian, R. 1977 The functional formalism of classical statistical dynamics. J. Phys. A 10, 777–789.CrossRefGoogle Scholar
Rai Choudhuri, A. 1998 The Physics of Fluids and Plasmas, an Introduction for Astrophysicists. Cambridge University Press.Google Scholar
Roberts, D. A. & Goldstein, M. L. 1991 Turbulence and waves in the solar wind. Rev. Geophys. 29, 932.CrossRefGoogle Scholar
Sahoo, G., Perlekar, P. & Pandit, R. 2011 Systematics of the magnetic-Prandtl-number dependence of homogeneous, isotropic magnetohydrodynamic turbulence. New J. Phys. 13, 013036.Google Scholar
Tetrault, D. 1992a Turbulent relaxation of magnetic field – 1. Coarse-grained dissipation and reconnection. J. Geophys. Res. 97, 8531–8540.Google Scholar
Tetrault, D. 1992b Turbulent relaxation of magnetic field – 2. Self-organization and intermittency. J. Geophys. Res. 97, 8541–8547.Google Scholar
Van Kampen, N. G. 1981 Ito versus Stratonovich. J. Stat. Phys. 24, 175–187.CrossRefGoogle Scholar
Verma, M. K., Roberts, D. A., Goldstein, M. L., Ghosh, S. & Stribling, W. T. 1996 A numerical study of the nonlinear cascade of energy in magnetohydrodynamic turbulence. J. Geophys. Res. 101, 21619.CrossRefGoogle Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Physica A 125, 150–162.Google Scholar
Volwerk, M., Vörös, Z., Baumjohann, W., Nakamura, R., Runov, A., Zhang, T. L., Glassmeier, K.-H., Treumann, R. A., Klecker, B., Balogh, A. et al. 2004 Multi-scale analysis of turbulence in the Earth’s current sheet. Ann. Geophys. 22, 2525–2533.Google Scholar
Vörös, Z., Baumjohann, W., Nakamura, R., Volwerk, M., Runov, A., Zhang, T. L., Eichelberger, H. U., Treumann, R. A., Georgescu, E., Balogh, A. et al. 2004 Magnetic turbulence in the plasma sheet. J. Geophys. Res. 109, A11215.Google Scholar
Warhaft, Z. 2002 Turbulence in nature and in the laboratory. Proc. Natl Acad. Sci. USA 99, 2481–2486.CrossRefGoogle ScholarPubMed
Wu, C. C. & Chang, T. 2000 Dynamical evolution of coherent structures in intermittent two-dimensional MHD turbulence. IEEE Trans. Plasma Sci. 28, 1938–1943.Google Scholar