Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T11:16:48.463Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and evolution of electromagnetic solitons in relativistic degenerate laser plasmas

Published online by Cambridge University Press:  10 December 2020

Sima Roy  and
A. P. Misra Open the ORCID record for A. P. Misra [Opens in a new window]
Sima Roy
Affiliation:
Department of Mathematics, Siksha Bhavana, Visva-Bharati (A Central University), Santiniketan731 235, India
A. P. Misra*
Affiliation:
Department of Mathematics, Siksha Bhavana, Visva-Bharati (A Central University), Santiniketan731 235, India
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamical behaviours of electromagnetic (EM) solitons formed due to nonlinear interaction of linearly polarized intense laser light and relativistic degenerate plasmas are studied. In the slow-motion approximation of relativistic dynamics, the evolution of weakly nonlinear EM envelope is described by the generalized nonlinear Schrödinger (GNLS) equation with local and nonlocal nonlinearities. Using the Vakhitov–Kolokolov criterion, the stability of an EM soliton solution of the GNLS equation is studied. Different stable and unstable regions are demonstrated with the effects of soliton velocity, soliton eigenfrequency, as well as the degeneracy parameter 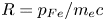$R=p_{Fe}/m_ec$, where 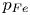$p_{Fe}$ is the Fermi momentum and 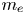$m_e$ the electron mass and 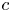$c$ is the speed of light in vacuum. It is found that the stability region shifts to an unstable one and is significantly reduced as one enters from the regimes of weakly relativistic 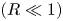$(R\ll 1)$ to ultrarelativistic 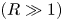$(R\gg 1)$ degeneracy of electrons. The analytically predicted results are in good agreement with the simulation results of the GNLS equation. It is shown that the standing EM soliton solutions are stable. However, the moving solitons can be stable or unstable depending on the values of soliton velocity, the eigenfrequency or the degeneracy parameter. The latter with strong degeneracy $(R>1)$ can eventually lead to soliton collapse.

Keywords

plasma nonlinear phenomenaplasma wavesastrophysical plasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 6 , December 2020 , 905860611
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berezhiani, V. I., Shatashvili, N. L. & Tsintsadze, N. L. 2015 Electromagnetic solitons in degenerate relativistic electron–positron plasma. Phys. Scr. 90, 068005.CrossRefGoogle Scholar
Bersons, I., Veilande, R. & Balcers, O. 2020 Model of compact 3D electromagnetic solitons. Phys. Scr. 95, 025203.CrossRefGoogle Scholar
Chandrasekhar, S. 1935 The highly collapsed configurations of a stellar mass (second paper). Mon. Not. R. Astron. Soc. 95, 207.CrossRefGoogle Scholar
Gratton, F. T., Gnavi, G., Galvao, R. M. O. & Gomberoff, L. 1997 Self-modulation of a strong electromagnetic wave in a positron-electron plasma induced by relativistic temperatures and phonon damping. Phys. Rev. E 55, 3381.CrossRefGoogle Scholar
Hadzievski, L. J., Jovanovic, M. S., Skoric, M. M. & Mima, K. 2002 Stability of one-dimensional electromagnetic solitons in relativistic laser plasmas. Phys. Plasmas 9, 2569.CrossRefGoogle Scholar
Hayes, A. C., Gooden, M. E., Henry, E., Jungman, G., Wilhelmy, J. B., Rundberg, R. S., Yeamans, C., Kyrala, G., Cerjan, C., Danielson, D. L., et al. 2020 Impact of free electron degeneracy on collisional rates in plasmas. Nat. Phys. 16, 432.CrossRefGoogle Scholar
Holkundkar, A. R. & Brodin, G. 2020 Transition from wakefield generation to soliton formation. Phys. Rev. E 97, 043204.Google Scholar
Jeong, T. M. & Lee, J. 2016 Generation of high-intensity laser pulses and their applications. doi:10.5772/64526.CrossRefGoogle Scholar
Lehmann, G., Laedke, E. W. & Spatschek, K. H. 2006 Stability and evolution of one-dimensional relativistic solitons on the ion time scale. Phys. Plasmas 13, 092302.CrossRefGoogle Scholar
Litvak, A. G. & Sergeev, A. M. 1978 One-dimensional collapse of plasma waves. JETP Lett. 27, 517.Google Scholar
Mancic, A., Hadzievski, L. & Skoric, M. M. 2006 Dynamics of electromagnetic solitons in a relativistic plasma. Phys. Plasmas 13, 052309.CrossRefGoogle Scholar
Mikaberidze, G. & Berezhiani, V. I. 2015 Standing electromagnetic solitons in degenerate relativistic plasmas. Phys. Lett. A 379, 2730.CrossRefGoogle Scholar
Misra, A. P. & Banerjee, S. 2011 Upper-hybrid wave-driven Alfvénic turbulence in magnetized dusty plasmas. Phys. Rev. E 83, 037401.CrossRefGoogle ScholarPubMed
Misra, A. P. & Chatterjee, D. 2018 Stimulated scattering instability in a relativistic plasma. Phys. Plasmas 25, 062116.CrossRefGoogle Scholar
Pelinovsky, E., Afanasijev, V. V. & Kivshar, Y. S. 1996 Nonlinear theory of oscillating, decaying, and collapsing solitons in the generalized nonlinear Schrödinger equation. Phys. Rev. E 53, 1940.CrossRefGoogle ScholarPubMed
Roy, S., Chatterjee, D. & Misra, A. P. 2020 Generation of wakefields and electromagnetic solitons in relativistic degenerate plasmas. Phys. Scr. 95, 015603.CrossRefGoogle Scholar
Sundar, S., Das, A., Saxena, V., Kaw, P. & Sen, A. 2011 Relativistic electromagnetic flat top solitons and their stability. Phys. Plasmas 18, 112112.CrossRefGoogle Scholar
Vakhitov, N. G. & Kolokolov, A. A. 1973 Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 16, 783–789.CrossRefGoogle Scholar
Verheest, F. 2015 Symmetries and charge neutrality of electromagnetic solitons in perfect pair plasmas. Phys. Scr. 90, 068002.CrossRefGoogle Scholar
Verheest, F. 2016 Perpendicular propagation of electromagnetic solitons in magnetized thermal pair plasmas. Phys. Scr. 91, 025603.CrossRefGoogle Scholar
Williams, G. O., Chung, H.-K., Künzel, S., Hilbert, V., Zastrau, U., Scott, H., Daboussi, S., Iwan, B., Gonzalez, A. I., Boutu, W., et al. 2019 Impact of free electron degeneracy on collisional rates in plasmas. Phys. Rev. Res. 1, 033216.CrossRefGoogle Scholar