Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T15:13:52.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Speculations about plasma free energy, 50 years later

Published online by Cambridge University Press:  22 September 2016

T. K. Fowler
T. K. Fowler*
Affiliation:
University of California, Berkeley, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Plasma free energy is that part of the total energy that feeds the growth of turbulence. The most successful free energy formulation in plasma physics is the MHD Energy Principle – successful because, within magnetohydrodynamics (MHD), the free energy 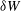$\unicode[STIX]{x1D6FF}W$ is both exact and self-adjoint (or Hermitian). A corresponding result in Vlasov theory is the free energy of equilibria neighbouring stable Maxwellian states – again giving a free energy of Hermitian form for the linearized equations. Since quantum mechanics is inherently Hermitian, here I speculate that quantum free energy is the ultimate way to understand classical plasma dynamics.

Keywords

Vlasov theoryfree energyPIC
Type
Tutorial
Information
Journal of Plasma Physics , Volume 82 , Issue 5 , October 2016 , 925820501
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernstein, I. B. 1958 Phys. Rev. 109, 10.Google Scholar
Bernstein, I. B., Frieman, E. A., Kruskal, M. D. & Kulsrud, R. M. 1958 An Energy Principle for hydromagnetic stability problems. Proc. R. Soc. Lond. A244, 17.Google Scholar
Brizard, A., Fowler, T. K., Hua, D. & Morrison, P. J. 1991 Thermodynamic constraints applied to tokamaks. Commun. Plasma Phys. Control. Fusion 14, 263–273.Google Scholar
Colgate, S. A., Fowler, T. K., Li, H., Hooper, E. B., McClenaghan, J. & Lin, Z. 2015 Quasi-static model of magnetically collimated jets and radiolobe. II. Jet structure and stability. Astrophys. J. 813, 136–155.Google Scholar
Dauger, D. E.2001 Semi-classical modeling of quantum mechanical multiparticle systems. PhD thesis, Department of Physics, UCLA.Google Scholar
Fowler, T. K. 1961 Stability of plasmaa against electrostatic perturbations. Phys. Fluids 4, 1393–1398.Google Scholar
Fowler, T. K. 1962 Theoretically stable and confined plasma. Phys. Fluids 5, 249–250.CrossRefGoogle Scholar
Fowler, T. K. 1963 Lyapunov’s stability criteria for plamas. J. Math. Phys. 4, 559–569.CrossRefGoogle Scholar
Fowler, T. K. 1964 Bounds on plasma instability growth rates. Phys. Fluids 7, 249.CrossRefGoogle Scholar
Fowler, T. K. 1968 Thermodynamics of unstable plasmas. In Advances in Plasma Physics (ed. Simon, A. & Thompson, W. B.), vol. 1.1, p. 201. Interscience Press, John Wiley & Sons.Google Scholar
Fowler, T. K. 1997 The Fusion Quest. chap. 7, Johns Hopkins University Press.Google Scholar
Freidberg, J. P. 2015 Ideal MHD. Cambridge University Press.Google Scholar
Goldberger, M. L. & Watson, K. M. 1964 Collision Theory. John Wiley & Sons.Google Scholar
Kadomtsev, B. B. 1965 Plasma Turbulence. Academic Press.Google Scholar
Krall, N. A. & Trivelpiece, A. W. 1973 Principles of Plasma Physics. chap. 2, McGraw-Hill.Google Scholar
Krolik, J. H. 1999 Active Galactic Nuclei. Princeton University Press.CrossRefGoogle Scholar
Kruskal, M. D. & Oberman, C. R. 1958 Phys. Fluids 1, 275.Google Scholar
LaSalle, J. & Lefschetz, S. 1961 Stability by Liapunov’s Direct Method. Academic.Google Scholar
Rosenbluth, M. N. & Rutherford, P. H. 1981 Tokamak plasma stability. In Fusion (ed. Teller, E.), vol. 1. chap. 2, Academic.Google Scholar
Rusbridge, M. G., Gee, S. J., Browning, P. K. et al. 1997 The design and operation of the SPHEX spheromak. Plasma Phys. Control. Fusion 39, 683–714.Google Scholar
Schiff, L. I. 1949 Quantum Mechanics. Mc-Graw Hill.Google Scholar
Taylor, J. B. 1986 Relaxation and magnetic reconnection in plasmas. Rev. Mod. Phys. 58, 741–763.CrossRefGoogle Scholar