Shielding of test charges in warm, isotropic electron and electron–ion (Te ≫ Ti) plasmas is studied analytically and numerically. For a plasma with hot Maxwellian electrons and cold mobile ions, the potential due to a charge moving faster than the ion acoustic velocity has an ion acoustic Cerenkov cone. Ahead of the particle, the shielding is the usual electron Debye type with a modified longer shielding length. Potential wells with γ−1 dependence exists inside the cone. 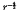The potential falls off as along the cone surface. Outside the cone, the potential decays exponentially. A charge moving slower than the ion acoustic velocity also creates a cone, with potential decay as γ−3 outside the cone, potential wells decaying as γ−1 inside the cone, and potential wells falling off as 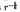along the cone surface. In both cases a radial logarithmic singularity exists along the trailing axis. Using a mono-energetic ion distribution, the singularity is removed and an ion thermal Cerenkov cone appears. For a monoenergetic electron plasma, assuming immobile ions, a test charge moving faster than the electron thermal velocity excites a thermal Cerenkov cone. Outside the cone, the far-field potential falls off in quadrupole form as γ−3. Inside the cone, potential wells decay as γ−1.