Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:19:27.856Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-consistent single mode investigations of the quasi-geostrophic convection-driven dynamo model

Part of: 50 years of Mean Field Electrodynamics

Published online by Cambridge University Press:  13 August 2018

Meredith Plumley ,
Michael A. Calkins ,
Keith Julien  and
Steven M. Tobias
Meredith Plumley*
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Michael A. Calkins
Affiliation:
Department of Physics, University of Colorado, Boulder, CO 80309, USA
Keith Julien
Affiliation:
Department of Applied Mathematics, University of Colorado, Boulder, CO 80309, USA
Steven M. Tobias
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The quasi-geostrophic dynamo model (QGDM) is a multiscale, fully nonlinear Cartesian dynamo model that is valid in the asymptotic limit of low Rossby number. In the additional limit of small magnetic Prandtl number investigated here, the QGDM is a self-consistent, asymptotically exact form of an 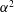$\unicode[STIX]{x1D6FC}^{2}$ large-scale dynamo. This article explores methods for simulating the multiscale QGDM and investigates how convection is altered by the magnetic field in the planetary regime of small Rossby number and small magnetic Prandtl number. At present, this combination is beyond the reach of direct numerical simulations. We use a simplified class of solutions whose horizontal structure is restricted to a periodic hexagonal lattice characterized by a single horizontal wavenumber (single mode). In contrast with previous kinematic investigations of the QGDM, the Lorentz force is included to study saturated, self-consistent dynamos. Two methodologies are used to assess handling of the multiple time scales of the QGDM: a stiff, common-in-time approach where all time scales are converted to a single time variable and a heterogeneous multiscale modelling approach employing fast time averaging on the Reynolds, magnetic and buoyancy eddy fluxes that feed back onto the slow scales. These strategies produce consistent results and each illustrates self-similar dynamics as the time-averaging window is increased. The properties of the convection are significantly altered by the dynamo-generated magnetic field. All solutions show a decrease in the overall heat transfer efficiency as compared to non-magnetic convection, suggesting that a change in length scale or flow planform plays a critical role in the enhanced heat transfer efficiency observed in previous dynamo studies. All dynamo solutions show a trend of increasing ohmic dissipation relative to viscous dissipation as the buoyancy forcing is increased.

Keywords

plasma dynamicsplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 4 , August 2018 , 735840406
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aurnou, J. & Olson, P. 2001 Experiments on Rayleigh–Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.Google Scholar
Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71.Google Scholar
Bassom, A. P. & Zhang, K. 1994 Strongly nonlinear convection cells in a rapidly rotating fluid layer. Geophys. Astrophys. Fluid Dyn. 76, 223–238.Google Scholar
Bushby, P. J., Käpylä, P. J., Masada, Y., Brandenburg, A., Favier, B., Guervilly, C. & Käpylä, M. J. 2018 Large-scale dynamos in rapidly rotating plane layer convection. Astron. Astrophys 612, A97.Google Scholar
Calkins, M. A. 2018 Quasi-geostrophic dynamo theory. Phys. Earth Planet. Inter. 276, 182–189.Google Scholar
Calkins, M. A., Julien, K. & Tobias, S. M. 2017 Inertia-less convectively-driven dynamo models in the limit of low Rossby number. Phys. Earth Planet. Inter. 266, 54–59.Google Scholar
Calkins, M. A., Julien, K., Tobias, S. M. & Aurnou, J. M. 2015 A multiscale dynamo model driven by quasi-geostrophic convection. J. Fluid Mech. 780, 143–166.Google Scholar
Calkins, M. A., Julien, K., Tobias, S. M., Aurnou, J. M. & Marti, P. 2016a Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers: single mode solutions. Phys. Rev. E 93, 023115.Google Scholar
Calkins, M. A., Long, L., Nieves, D., Julien, K. & Tobias, S. M. 2016b Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers. Phys. Rev. Fluids 1, 083701.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geofys. Publ. 17, 3–17.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28 (6), 1087–1095.Google Scholar
Childress, S. & Soward, A. M. 1972 Convection-driven hydromagnetic dynamo. Phys. Rev. Lett. 29 (13), 837–839.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166 (1), 97–114.Google Scholar
Cioni, S., Chaumat, S. & Sommeria, J. 2000 Effect of a vertical magnetic field on turbulent Rayleigh–Bénard convection. Phys. Rev. E 62 (4), R4520.Google Scholar
E, W., Engquist, B., Li, X., Ren, W. & Vanden-Eijnden, E. 2007 Heterogeneous multiscale methods: a review. Commun. Comput. Phys. 2 (3), 367–450.Google Scholar
Elsasser, W. M. 1956 Hydromagnetic dynamo theory. Rev. Mod. Phys. 28 (2), 135.Google Scholar
Fearn, D. R. 1979 Thermally driven hydromagnetic convection in a rapidly rotating sphere. Proc. R. Soc. Lond. A 369, 227–242.Google Scholar
Finlay, C. C. & Amit, H. 2011 On flow magnitude and field-flow alignment at Earth’s core surface. Geophys. J. Intl 186, 175–192.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Greer, B. J., Hindman, B. W., Featherstone, N. A. & Toomre, J. 2015 Helioseismic imaging of fast convective flows throughout the near-surface shear layer. Astrophys. J. Lett. 803 (2), L17.Google Scholar
Hanosage, S. M., Duvall, T. L. & Sreenivasan, K. R. 2012 Anomalously weak solar convection. Proc. Natl Acad. Sci. USA 109 (30), 11928–11932.Google Scholar
Haut, T. & Wingate, B. 2014 An asymptotic parallel-in-time method for highly oscillatory pdes. SIAM J. Sci. Comput. 36 (2), A693–A713.Google Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.Google Scholar
Julien, K., Aurnou, J., Calkins, M., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.Google Scholar
Julien, K. & Knobloch, E. 1998 Strongly nonlinear convection cells in a rapidly rotating fluid layer: the tilted $f$ -plane. J. Fluid Mech. 360, 141–178.Google Scholar
Julien, K. & Knobloch, E. 1999 Fully nonlinear three-dimensional convection in a rapidly rotating layer. Phys. Fluids 11 (6), 1469–1483.Google Scholar
Julien, K., Knobloch, E., Milliff, R. & Werne, J. 2006 Generalized quasi-geostrophy for spatially anisotropic rotationally constrained flows. J. Fluid Mech. 555, 233–274.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 254503.Google Scholar
Julien, K., Knobloch, E. & Tobias, S. M. 1999 Strongly nonlinear magnetoconvection in three dimensions. Physica D 128, 105–129.Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.Google Scholar
Julien, K. & Watson, M. 2009 Efficient multi-dimensional solution of PDEs using Chebyshev spectral methods. J. Comput. Phys. 228, 1480–1503.Google Scholar
King, E. M. & Aurnou, J. M. 2013 Turbulent convection in liquid metal with and without rotation. Proc. Natl Acad. Sci. USA 110 (17), 6688–6693.Google Scholar
Malecha, Z., Chini, G. & Julien, K. 2014 A multiscale algorithm for simulating spatially-extended Langmuir circulation dynamics. J. Comput. Phys. 271, 131–150.Google Scholar
Matthews, P. C. 1999 Asymptotic solutions for nonlinear magnetoconvection. J. Fluid Mech. 387, 397–409.Google Scholar
Mizerski, K. A. & Tobias, S. M. 2013 Large-scale convective dynamos in a stratified rotating plane layer. Geophys. Astrophys. Fluid Dyn. 107, 218–243.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Ossendrijver, M. 2003 The solar dynamo. Astron. Astrophys. Rev. 11, 287–367.Google Scholar
Parker, E. N. 1955 Hydromagnetic dynamo models. Astrophys. J. 122, 293–314.Google Scholar
Pedlosky, J. 1992 Geophysical Fluid Dynamics. Springer.Google Scholar
Peyret, R. 2013 Spectral Methods for Incompressible Viscous Flow. Springer Science & Business Media.Google Scholar
Pozzo, M., Davies, C. J., Gubbins, D. & Alfé, D. 2013 Transport properties for liquid silicon–oxygen–iron mixtures at Earth’s core conditions. Phys. Rev. B 87, 014110.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid posessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211, 1–29.Google Scholar
Schubert, G. & Soderlund, K. M. 2011 Planetary magnetic fields: Observations and models. Phys. Earth Planet. Inter. 187 (3), 92–108.Google Scholar
Soward, A. M. 1974 A convection-driven dynamo: I. The weak field case. Phil. Trans. R. Soc. Lond. A 275, 611–646.Google Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.Google Scholar
Stellmach, S. & Hansen, U. 2004 Cartesian convection driven dynamos at low Ekman number. Phys. Rev. E 70 (5), 056312.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104, 213–218.Google Scholar
Tilgner, A. 2014 Magnetic energy dissipation and mean magnetic field generation in planar convection-driven dynamos. Phys. Rev. E 90, 013004.Google Scholar
Tobias, S. M., Cattaneo, F. & Boldyrev, S. 2011 MHD dynamos and turbulence. In Ten Chapters in Turbulence. Cambridge University Press.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar