Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T19:17:15.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced magneto-hydrodynamic theory of coherent magnetic chains in the solar wind

Part of: Focus on Space Plasmas Professor Francesco Pegoraro

Published online by Cambridge University Press:  08 August 2018

Dušan Jovanović ,
Olga Alexandrova ,
Milan Maksimović  and
Milivoj Belić
Dušan Jovanović*
Affiliation:
Institute of Physics, University of Belgrade, Pregrevica 118, 11080 Belgrade (Zemun), Serbia State University of Novi Pazar, Vuka Karadžića bb, 36300 Novi Pazar, Serbia
Olga Alexandrova
Affiliation:
Observatoire de Paris–Meudon, Laboratoire d’Etudes Spatiales et d’Instrumentation en Astrophysique (LESIA), Centre National de la Recherche Scientifique (CNRS), 5 place J. Janssen, 92190 Meudon, France
Milan Maksimović
Affiliation:
Observatoire de Paris–Meudon, Laboratoire d’Etudes Spatiales et d’Instrumentation en Astrophysique (LESIA), Centre National de la Recherche Scientifique (CNRS), 5 place J. Janssen, 92190 Meudon, France
Milivoj Belić
Affiliation:
Texas A&M University at Qatar, P.O. Box 23874 Doha, Qatar
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An analytic theory is presented of magnetic structures in collisionless, high-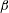$\unicode[STIX]{x1D6FD}$ plasmas. Using a reduced magnetohydrodynamic model, a stationary nonlinear solution is constructed in the form of a Kelvin–Stuart cat’s eyes chain of magnetic islands, on the spatial scale that exceeds the characteristic ion lengths. The solution is imbedded in a background current sheet and possesses both a significant plasma density perturbation trapped inside the magnetic islands and a compressional magnetic field component that is driven mostly by a current loop located at the separatrix of the islands. This theory may provide an explanation for the magnetic structures observed in the solar wind close to the Earth by the Cluster spacecraft.

Keywords

astrophysical plasmasplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 4 , August 2018 , 725840402
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexandrova, O., Mangeney, A., Maksimovic, M., Cornilleau-Wehrlin, N., Bosqued, J.-M. & André, M. 2006 Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. 111, A12208.Google Scholar
Alexandrova, O. & Saur, J. 2008 Alfvén vortices in Saturn’s magnetosheath: Cassini observations. Geophys. Res. Lett. 35, L15102.Google Scholar
Balogh, A., Carr, C. M., Acuña, M. H., Dunlop, M. W., Beek, T. J., Brown, P., Fornaçon, K.-H., Georgescu, E., Glassmeier, K.-H., Harris, J. et al. 2001 The cluster magnetic field investigation: overview of in-flight performance and initial results. Ann. Geophys. 19, 1207–1217.Google Scholar
Cafaro, E., Grasso, D., Pegoraro, F., Porcelli, F. & Saluzzi, A. 1998 Invariants and geometric structures in nonlinear Hamiltonian magnetic reconnection. Phys. Rev. Lett. 80, 4430–4433.Google Scholar
Cerri, S. S. & Califano, F. 2017 Reconnection and small-scale fields in 2D-3V hybrid-kinetic driven turbulence simulations. New J. Phys. 19 (2), 025007.Google Scholar
Cornilleau-Wehrlin, N., Chanteur, G., Perraut, S., Rezeau, L., Robert, P., Roux, A., de Villedary, C., Canu, P., Maksimovic, M., de Conchy, Y. et al. 2003 First results obtained by the Cluster STAFF experiment. Ann. Geophys. 21, 437–456.Google Scholar
Eyink, G. L., Lazarian, A. & Vishniac, E. T. 2011 Fast magnetic reconnection and spontaneous stochasticity. Astrophys. J. 743, 51.Google Scholar
Hesse, M., Neukirch, T., Schindler, K., Kuznetsova, M. & Zenitani, S. 2011 The diffusion region in collisionless magnetic reconnection. Space Sci. Rev. 160, 3–23.Google Scholar
Jovanovic, D., Alexandrova, O., Maksimovic, M. & Belic, M.2017 Fluid theory of coherent magnetic vortices in high-beta space plasmas. Preprint, arXiv:1705.02913.Google Scholar
Jovanović, D. & Horton, W. 1994 On the stability of shear-Alfvén vortices. Phys. Plasmas 1, 2614–2622.Google Scholar
Jovanovic, D., Pecseli, H. L., Rasmussen, J. J. & Thomsen, K. 1987 Modified convective cells in plasmas. J. Plasma Phys. 37, 81–95.Google Scholar
Jovanović, D. & Pegoraro, F. 1998 Coherent nonlinear electromagnetic drift-mode structures. Phys. Scr. T 75, 182–185.Google Scholar
Jovanovic, D. & Vranjes, J. 1994 Nonlinear vortex chain associated with tearing mode. Phys. Plasmas 1, 3239–3245.Google Scholar
Kadomtsev, B. B. & Pogutse, O. P. 1974 Convection of plasma in the tokamak. Sov. J. Exp. Theoret. Phys. 66, 2056.Google Scholar
Kadomtsev, B. B. & Pogutse, O. P. 1973 Nonlinear helical perturbations of a plasma in the tokamak. Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki 65, 575–589.Google Scholar
Lion, S., Alexandrova, O. & Zaslavsky, A. 2016 Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophys. J. 824, 47.Google Scholar
Morrison, P. J., Caldas, I. L. & Tasso, H. 1984 Hamiltonian formulation of two-dimensional gyroviscous MHD. Zeitschrift Naturforschung Teil A 39, 1023–1027.Google Scholar
Morrison, P. J. & Greene, J. M. 1980 Noncanonical Hamiltonian density formulation of hydrodynamics and ideal magnetohydrodynamics. Phys. Rev. Lett. 45, 790–794.Google Scholar
Morrison, P. J. & Hazeltine, R. D. 1984 Hamiltonian formulation of reduced magnetohydrodynamics. Phys. Fluids 27, 886–897.Google Scholar
Muñoz, P. R., Chian, A. C.-L., Miranda, R. A. & Yamada, M. 2010 Observation of magnetic reconnection and current sheets in the solar wind. In Solar and Stellar Variability: Impact on Earth and Planets (ed. Kosovichev, A. G., Andrei, A. H. & Rozelot, J.-P.), IAU Symposium, vol. 264, pp. 369–372. Cambridge University Press.Google Scholar
Perrone, D., Alexandrova, O., Mangeney, A., Maksimovic, M., Lacombe, C., Rakoto, V., Kasper, J. C. & Jovanovic, D. 2016 Compressive coherent structures at ion scales in the slow solar wind. Astrophys. J. 826, 196.Google Scholar
Perrone, D., Alexandrova, O., Roberts, O. W., Lion, S., Lacombe, C., Walsh, A., Maksimovic, M. & Zouganelis, I. 2017 Coherent structures at ion scales in fast solar wind: cluster observations. Astrophys. J. 849, 49.Google Scholar
Polyanin, A. D. & Zaitsev, V. F. 2012 Subsection 5.4.1 in Handbook of Nonlinear Partial Differential Equations. Chapman & Hall/CRC Press.Google Scholar
Porcelli, F., Borgogno, D., Califano, F., Grasso, D. & Pegoraro, F. 2004 Magnetic reconnection: collisionless regimes. Phys. Scr. T 107, 153.Google Scholar
del Sarto, D., Califano, F. & Pegoraro, F. 2003 Secondary instabilities and vortex formation in collisionless-fluid magnetic reconnection. Phys. Rev. Lett. 91 (23), 235001.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310–377.Google Scholar
Schep, T. J., Pegoraro, F. & Kuvshinov, B. N. 1994 Generalized two-fluid theory of nonlinear magnetic structures. Phys. Plasmas 1, 2843–2852.Google Scholar
Strauss, H. R. 1976 Nonlinear, three-dimensional magnetohydrodynamics of noncircular tokamaks. Phys. Fluids 19, 134–140.Google Scholar
Strauss, H. R. 1977 Dynamics of high beta Tokamaks. Phys. Fluids 20, 1354–1360.Google Scholar
Zweibel, E. G. & Yamada, M. 2016 Perspectives on magnetic reconnection. Proc. R. Soc. Lond. A 472, 20160479.Google Scholar