Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T15:20:59.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of a plasma beam entering transverse magnetic fields

Published online by Cambridge University Press:  13 March 2009

J. Koga ,
J. L. Geary ,
T. Fujinami ,
B. S. Newberger ,
T. Tajima  and
N. Rostoker
J. Koga
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
J. L. Geary
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
T. Fujinami
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
B. S. Newberger
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
T. Tajima
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
N. Rostoker
Affiliation:
Department of Physics, University of California, Irvine, California 92717, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study plasma-beam injection into transverse magnetic fields using both electrostatic and electromagnetic particle-in-cell (PIC) codes. In the case of small beam momentum or energy (low drift kinetic β) we study both large- and small-ion-gyroradius beams. Large-ion-gyroradius beams with a large dielectric constant ε ≫ (M/m)½ are found to propagate across the magnetic field via E × B drifts at nearly the initial injection velocity, where 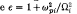and M/m is the ion-to-electron mass ratio. Beam degradation and undulations are observed, in agreement with previous experimental and analytical results. When ε is of order (M/m)½ the plasma beam propagates across field lines at only half its initial velocity and loses its coherent structure. When ε is much less than (M/m)½ the beam particles decouple at the magnetic field boundary, scattering the electrons and slightly deflecting the ions. For small-ion-gyroradius beam injection a flute-type instability is observed at the beam-magnetic-field interface. In the case of large beam momentum or energy (high drift kinetic β) we observe good penetration of a plasma beam by shielding the magnetic field from the interior of the beam (diamagnetism). However, we observe anomalously fast penetration of the magnetic field into the beam and find that the diffusion rate depends on the electron gyroradius of the beam.

Type
Research Article
Information
Journal of Plasma Physics , Volume 42 , Issue 1 , August 1989 , pp. 91 - 110
Copyright
Copyright © Cambridge University Press 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baker, D. A. & Hammel, J. E. 1962 Phys. Rev. Lett. 8, 157.CrossRefGoogle Scholar
Birdsall, G. K. & Langdon, A. B. 1985 Plasma Physics via Computer Simulation. McCraw-Hill.Google Scholar
Bostick, W. H. 1956 Phys. Rev. 104, 292.CrossRefGoogle Scholar
Chapman, S. & Ferraro, V. C. A. 1931 J. Geophys. Res. 36, 77.Google Scholar
Dawson, J. M. 1983 Rev. Mod. Phys. 55, 403.CrossRefGoogle Scholar
Felber, F. S., Hunter, R. O., Pereira, N. R. & Tajima, T. 1982 Appl. Phys. Lett. 41, 705.CrossRefGoogle Scholar
Galvez, M. 1987 Phys. Fluids, 30, 2729.CrossRefGoogle Scholar
Galvez, M. & Barnes, C. 1988 Phys. Fluids, 31, 863.CrossRefGoogle Scholar
Galvez, M., Gary, S. P., Barnes, C. & Winske, D. 1988 Phys. Fluids, 31, 1554.CrossRefGoogle Scholar
Haerendel, G. & Sagdeev, R. Z. 1981 Adv. Space Res. 1, 29.CrossRefGoogle Scholar
Hockney, R. & Eastwood, J. W. 1981 Computer Simulation Using Particles. McGraw-Hill.Google Scholar
Humanic, D. G., Goede, H. & Dawson, J. M. 1982 Phys. Fluids, 25, 271.CrossRefGoogle Scholar
Ishizuka, H. & Robertson, S. 1982 Phys. Fluids, 25, 2353.CrossRefGoogle Scholar
Lindberg, L. 1978 Astrophys. Space Sci. 55, 203.CrossRefGoogle Scholar
Mishin, E. V., Treumann, R. A. & Kapitanov, V. Y. 1986 J. Geophys. Res. 91, 10183.CrossRefGoogle Scholar
Ott, E. & Manheimer, W. M. 1977 Nucl. Fusion, 17, 1057.CrossRefGoogle Scholar
Papadopoulos, K., Mankofsky, A. & Drobot, A. 1988 Phys. Rev. Lett. 61, 94.CrossRefGoogle Scholar
Peter, W. 1981 Plasma Motion A cross a Magnetic Field. Ph.D. dissertation, University of California, Irvine.Google Scholar
Peter, W., Ron, A. & Rostoker, N. 1979 Phys. Fluids, 22, 1471.CrossRefGoogle Scholar
Peter, W. & Rostoker, N. 1982 Phys. Fluids, 25, 730.CrossRefGoogle Scholar
Ripin, B. H., McLean, E. A., Manka, C. K., Pawley, C., Stamper, J. A., Peyser, T. A., Mostovych, A. N., Grun, J., Hassam, A. B. & Huba, J. D. 1987 Phys. Rev. Lett. 59, 2299.CrossRefGoogle Scholar
Rosenbluth, M. N., Krall, N. A. & Rostoker, N. 1962 Nucl. Fusion Suppl. part 1, p. 143.Google Scholar
Schmidt, G. 1960 Phys. Fluids, 3, 961.CrossRefGoogle Scholar
Sinelnikov, K. D. & Rutkevich, B. N. 1967 Soviet Phys. Tech. Phys. 12, 37.Google Scholar
Tajima, T. 1989 Computational Plasma Physics. Addison-Wesley.Google Scholar
Treumann, R. A. & Hausler, B. 1985 Astrophys. Space Sci. 110, 371.CrossRefGoogle Scholar
Wessel, F., Hong, R., Song, J., Fisher, A., Rostoker, N., Ron, A., Li, R. & Fan, R. Y. 1988 Phys. Fluids, 31, 3778.CrossRefGoogle Scholar
Wessel, F. & Robertson, S. 1981 Phys. Fluids, 24, 739.CrossRefGoogle Scholar
Winglee, R. M. & Pritchett, P. L. 1987 J. Geophys. Res. 92, 7689.CrossRefGoogle Scholar
Winske, D. 1988 J. Geophys. Res. 93, 2539.CrossRefGoogle Scholar