Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-09T14:59:48.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-diffusive angular momentum transport in rotating $z$-pinches

Published online by Cambridge University Press:  04 November 2019

G. Rüdiger Open the ORCID record for G. Rüdiger [Opens in a new window]  and
M. Schultz
G. Rüdiger*
Affiliation:
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, D-14482 Potsdam, Germany University of Potsdam, Institute of Physics and Astronomy, Karl-Liebknecht-Str. 24-25, 14476 Potsdam, Germany
M. Schultz
Affiliation:
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, D-14482 Potsdam, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of conducting Taylor–Couette flows under the presence of toroidal magnetic background fields is considered. For strong enough magnetic amplitudes such magnetohydrodynamic flows are unstable against non-axisymmetric perturbations which may also transport angular momentum. In accordance with the often used diffusion approximation, one expects the angular momentum transport to be vanishing for rigid rotation. In the sense of a non-diffusive 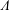$\unicode[STIX]{x1D6EC}$ effect, however, even for rigidly rotating $z$-pinches, an axisymmetric angular momentum flux appears which is directed outward (inward) for large (small) magnetic Mach numbers. The internal rotation in a magnetized rotating tank can thus never be uniform. Those particular rotation laws are used to estimate the value of the instability-induced eddy viscosity for which the non-diffusive 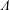$\unicode[STIX]{x1D6EC}$ effect and the diffusive shear-induced transport compensate each other. The results provide the Shakura & Sunyaev viscosity ansatz leading to numerical values linearly growing with the applied magnetic field.

Keywords

plasma instabilitiesastrophysical plasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 6 , December 2019 , 905850601
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boussinesq, M. 1897 Theorie de lecoulement tourbillonnant et tumultueux des liquides dans les lits rectilignes a grande section. Gauthier-Villars.Google Scholar
Chan, K. L. 2001 Rotating convection in F-planes: mean flow and Reynolds stress. Astrophys. J. 548, 1102–1117.Google Scholar
Chandrasekhar, S. 1956 On the stability of the simplest solution of the equations of hydromagnetics. Proc. Natl Acad. Sci. USA 42, 273–276.Google Scholar
Charbonneau, P. & MacGregor, K. B. 1992 Angular momentum transport in magnetized stellar radiative zones. I. Numerical solutions to the core spin-up model problem. Astrophys. J. 387, 639–661.Google Scholar
Deguchi, K. 2017 Linear instability in Rayleigh-stable Taylor–Couette flow. Phys. Rev. E 95 (2), 021102.Google Scholar
Elstner, D., Beck, R. & Gressel, O. 2014 Do magnetic fields influence gas rotation in galaxies? Astron. Astrophys. 568, A104.Google Scholar
Herron, I. & Soliman, F. 2006 The stability of Couette flow in a toroidal magnetic field. Appl. Math. Lett. 19, 1113–1117.Google Scholar
Hupfer, C., Käpylä, P. J. & Stix, M. 2006 Reynolds stresses and meridional circulation from rotating cylinder simulations. Astron. Astrophys. 459, 935–944.Google Scholar
Ji, H., Goodman, J. & Kageyama, A. 2001 Magnetorotational instability in a rotating liquid metal annulus. Mon. Not. R. Astron. Soc. 325, L1–L5.Google Scholar
Käpylä, P. J. 2019 Magnetic and rotational quenching of the $\unicode[STIX]{x1D6EC}$ effect. Astron. Astrophys. 622, A195.Google Scholar
Kirillov, O. N. & Stefani, F. 2013 Extending the range of the inductionless magnetorotational instability. Phys. Rev. Lett. 111 (6), 061103.Google Scholar
Ogilvie, G. I. & Pringle, J. E. 1996 The non-axisymmetric instability of a cylindrical shear flow containing an azimuthal magnetic field. Mon. Not. R. Astron. Soc. 279, 152–164.Google Scholar
Pitts, E. & Tayler, R. J. 1985 The adiabatic stability of stars containing magnetic fields. IV. The influence of rotation. Mon. Not. R. Astron. Soc. 216, 139–154.Google Scholar
Pringle, J. E. 1981 Accretion discs in astrophysics. Annu. Rev. Astron. Astrophys. 19, 137–162.Google Scholar
Rüdiger, G., Gellert, M., Hollerbach, R., Schultz, M. & Stefani, F. 2018 Stability and instability of hydromagnetic Taylor–Couette flows. Phys. Rep. 741, 1–89.Google Scholar
Rüdiger, G., Hollerbach, R., Schultz, M. & Elstner, D. 2007 Destabilization of hydrodynamically stable rotation laws by azimuthal magnetic fields. Mon. Not. R. Astron. Soc. 377, 1481–1487.Google Scholar
Rüdiger, G. & Kitchatinov, L. L. 1996 The internal solar rotation in its spin-down history. Astrophys. J. 466, 1078.Google Scholar
Rüdiger, G. & Shalybkov, D. A.2001 MHD Instability in cylindric Taylor–Couette flow. 12th International Couette-Taylor Workshop, Evanston 2001, arXiv:astro-ph/0108035.Google Scholar
Rüdiger, G. & Zhang, Y. 2001 MHD instability in differentially-rotating cylindric flows. Astron. Astrophys. 378, 302–308.Google Scholar
Seilmayer, M., Galindo, V., Gerbeth, G., Gundrum, T., Stefani, F., Gellert, M., Rüdiger, G., Schultz, M. & Hollerbach, R. 2014 Experimental evidence for nonaxisymmetric magnetorotational instability in a rotating liquid metal exposed to an azimuthal magnetic field. Phys. Rev. Lett. 113 (2), 024505.Google Scholar
Seilmayer, M., Stefani, F., Gundrum, T., Weier, T., Gerbeth, G., Gellert, M. & Rüdiger, G. 2012 Experimental evidence for a transient Tayler instability in a cylindrical liquid–metal column. Phys. Rev. Lett. 108 (24), 244501.Google Scholar
Shakura, N. I. & Sunyaev, R. A. 1973 Black holes in binary systems. Observational appearance. Astron. Astrophys. 24, 337–355.Google Scholar
Stefani, F. & Kirillov, O. N. 2015 Destabilization of rotating flows with positive shear by azimuthal magnetic fields. Phys. Rev. E 92 (5), 051001.Google Scholar
Tataronis, J. A. & Mond, M. 1987 Magnetohydrodynamic stability of plasmas with aligned mass flow. Phys. Fluids 30, 84–89.Google Scholar
Tayler, R. J. 1957 Hydromagnetic instabilities of an ideally conducting fluid. Proc. Phys. Soc. B 70, 31–48.Google Scholar
Tayler, R. J. 1973 The adiabatic stability of stars containing magnetic fields-I. Toroidal fields. Mon. Not. R. Astron. Soc. 161, 365.Google Scholar
Velikhov, E. 1959 Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. Sov. Phys. JETP 36, 1389–1404.Google Scholar