Article contents
Modulationally stable envelope solitons in astrophysical magnetoplasmas with degenerate relativistic electrons
Published online by Cambridge University Press: 28 October 2015
Abstract
The formation and propagation characteristics of small-amplitude magnetoacoustic dark/grey solitons are investigated in a semi relativistic degenerate magnetoplasma whose constituents are electrons and singly ionized positive ions. For this purpose, the electrons are assumed to follow the degeneracy pressure law through the Chandrasekhar equation of state, while the inertial cold ions are taken as non-degenerate and magnetized. By solving the one-fluid quantum magnetohydrodynamic (QMHD) model with the aid of a reductive perturbation technique, a nonlinear Schrödinger (NLS) equation is derived for weakly nonlinear envelope magnetoacoustic solitons. The NLS equation admits the existence of stable excitations, e.g. dark and grey solitons for which the condition  $P/Q<0$ holds. Numerical results reveal that the variation of plasma number density, magnetic field strength, relativistic parameter
$P/Q<0$ holds. Numerical results reveal that the variation of plasma number density, magnetic field strength, relativistic parameter 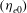 $({\it\eta}_{e0})$ and the quantum parameter
$({\it\eta}_{e0})$ and the quantum parameter 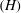 $(H)$ significantly modify the profiles of the envelope magnetoacoustic solitons. The present results are important to understanding of the nonlinear dynamics of magnetoacoustic solitons in astrophysical dense magnetoplasmas (viz., white dwarfs, magnetars, neutron stars, etc.), where the relativistic degeneracy effects play a vital role in collective interactions.
$(H)$ significantly modify the profiles of the envelope magnetoacoustic solitons. The present results are important to understanding of the nonlinear dynamics of magnetoacoustic solitons in astrophysical dense magnetoplasmas (viz., white dwarfs, magnetars, neutron stars, etc.), where the relativistic degeneracy effects play a vital role in collective interactions.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2015
References
- 3
- Cited by


