Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T15:57:51.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal perturbation flows that trigger mean field dynamos in shear flows

Part of: 50 years of Mean Field Electrodynamics

Published online by Cambridge University Press:  01 June 2018

W. Herreman
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a variational optimization method we find the smallest flow perturbations that can trigger kinematic dynamo action in Kolmogorov flow. In comparison to previous work, a second-order mean field dynamo model is used to track down the optimal dynamos in the high magnetic Reynolds number limit (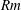$Rm$). The magnitude of minimal perturbation flows decays inversely proportional to the magnetic Reynolds number. We reveal the asymptotic high-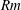$Rm$ structure of the optimal flow perturbation and the magnetic eigenmode. We identify the optimal dynamo as of $\unicode[STIX]{x1D6FC}{-}\unicode[STIX]{x1D6FA}$ type, with magnetic fluctuations that localize on a critical layer.

Keywords

plasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 3 , June 2018 , 735840305
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben-Dov, G. & Cohen, J. 2007 Critical Reynolds number for a natural transition to turbulence in pipe flows. Phys. Rev. Lett. 98, 064503.CrossRefGoogle ScholarPubMed
Biau, D. & Bottaro, A. 2009 An optimal path to transition in a duct. Phil. Trans. R. Soc. Lond. A 367 (1888), 529–544.Google Scholar
Braginsky, S. 1964 Self excitation of a magnetic field during the motion of a highly conducting fluid. Sov. Phys. JETP 20, 726–735.Google Scholar
Braginsky, S. & Roberts, P. 1975 Magnetic field generation by baroclinic waves. Proc. R. Soc. Lond. A 347 (1648), 125–140.Google Scholar
Chapman, S. J. 2002 Subcritical transition in channel flows. J. Fluid Mech. 451, 35–97.Google Scholar
Chen, L., Herreman, W. & Jackson, A. 2015 Optimal dynamo action by steady flows confined to a cube. J. Fluid Mech. 783, 23–45.Google Scholar
Chen, L., Herreman, W., Li, K., Livermore, P. W., Luo, J. W. & Jackson, A. 2018 The optimal kinematic dynamo driven by steady flows in a sphere. J. Fluid Mech. 839, 1–32.Google Scholar
Cherubini, S., Palma, P. D. & Robinet, J.-C. 2015 Nonlinear optimals in the asymptotic suction boundary layer: transition thresholds and symmetry breaking. Phys. Fluids 27 (3), 034108.Google Scholar
Deguchi, K. & Hall, P. 2015 Asymptotic descriptions of oblique coherent structures in shear flows. J. Fluid Mech. 782, 356–367.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Duguet, Y., Brandt, L. & Larsson, B. R. J. 2010 Towards minimal perturbations in transitional plane Couette flow. Phys. Rev. E 82 (2), 026316.Google Scholar
Guseva, A., Hollerbach, R., Willis, A. P. & Avila, M. 2017 Dynamo action in a quasi-Keplerian Taylor–Couette flow. Phys. Rev. Lett. 119, 164501.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Herault, J., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P.-Y. 2011 Periodic magnetorotational dynamo action as a prototype of nonlinear magnetic-field generation in shear flows. Phys. Rev. E 84, 036321.Google Scholar
Herreman, W. 2016 Minimal flow perturbations that trigger kinematic dynamo in shear flows. J. Fluid Mech. 795, R1.Google Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91 (24), 244502.CrossRefGoogle Scholar
Kerswell, R. 2018 Nonlinear nonmodal stability theory. Annu. Rev. Fluid Mech. 50 (1), 319–345.Google Scholar
Krause, F. & Rädler, K.-H. 1980 Mean-field Magnetohydrodynamics and Dynamo. Akademié and Pergamon.Google Scholar
Mellibovsky, F. & Meseguer, A. 2007 Pipe flow transition threshold following localized impulsive perturbations. Phys. Fluids 19 (4), 044102.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Peixinho, J. & Mullin, T. 2007 Finite-amplitude thresholds for transition in pipe flow. J. Fluid Mech. 582, 169–178.CrossRefGoogle Scholar
Pralits, J., Bottaro, A. & Cherubini, S. 2015 Weakly nonlinear optimal perturbations. J. Fluid Mech. 785, 135–151.Google Scholar
Rincon, F., Ogilvie, G. I. & Proctor, M. R. E. 2007 Self-sustaining nonlinear dynamo process in Keplerian shear flows. Phys. Rev. Lett. 98 (25), 254502.Google Scholar
Rincon, F., Ogilvie, G. I., Proctor, M. R. E. & Cossu, C. 2008 Subcritical dynamos in shear flows. Astron. Nachr. 329 (7), 750–761.Google Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G. I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.Google Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P.-Y. 2015 Dissipative effects on the sustainment of a magnetorotational dynamo in Keplerian shear flow. Astron. Astrophys. 575, A14.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.CrossRefGoogle ScholarPubMed
Willis, A. P. 2012 Optimization of the magnetic dynamo. Phys. Rev. Lett. 109 (25), 251101.Google Scholar
Zel’dovich, Y. B. 1957 The magnetic field in the two-dimensional motion of a conducting turbulent fluid. Sov. Phys. JETP 4, 460–462.Google Scholar