Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T14:43:01.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetoacoustic solitons and shocks in dense astrophysical plasmas with relativistic degenerate electrons

Published online by Cambridge University Press:  01 February 2016

M. Irfan ,
S. Ali  and
Arshad M. Mirza
M. Irfan*
Affiliation:
University of Malakand at Khyber Pakhtunkhwa, Dir (L) 18800, Pakistan Theoretical Plasma Physics Group, Department of Physics, Quaid-i-Azam University, Islamabad 45320, Pakistan National Centre for Physics at QAU Campus, Shahdra Valley Road, Islamabad 44000, Pakistan
S. Ali
Affiliation:
National Centre for Physics at QAU Campus, Shahdra Valley Road, Islamabad 44000, Pakistan
Arshad M. Mirza
Affiliation:
Theoretical Plasma Physics Group, Department of Physics, Quaid-i-Azam University, Islamabad 45320, Pakistan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two-fluid quantum magnetohydrodynamic (QMHD) equations are employed to investigate linear and nonlinear properties of the magnetosonic waves in a semi-relativistic dense plasma accounting for degenerate relativistic electrons. In the linear analysis, a plane wave solution is used to derive the dispersion relation of magnetosonic waves, which is significantly modified due to relativistic degenerate electrons. However, for a nonlinear investigation of solitary and shock waves, we employ the reductive perturbation technique for the derivation of Korteweg–de Vries (KdV) and Korteweg–de Vries Burger (KdVB) equations, admitting nonlinear wave solutions. Numerically, it is shown that the wave frequency decreases to attain a lowest possible value at a certain critical number density 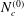$N_{c}^{(0)}$, and then increases beyond 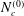$N_{c}^{(0)}$ as the plasma number density increases. Moreover, the relativistic electrons and associated pressure degeneracy lead to a reduction in the spatial extents of the magnetosonic waves and a strengthening of the shock amplitude. The results might be important for understanding the linear and nonlinear magnetosonic excitations in dense astrophysical plasmas, such as in white dwarfs, magnetars and neutron stars, etc., where relativistic degenerate electrons are present.

Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 1 , February 2016 , 905820106
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adlam, J. H. & Allen, J. E. 1958 The structure of strong collision-free hydromagnetic waves. Phil. Mag. 3, 448–455.CrossRefGoogle Scholar
Chakraborty, D. & Das, K. P. 2000 Evolution of nonlinear magnetosonic waves propagating obliquely to an external magnetic field in a collisionless plasma. J. Plasma Phys. 64, 211–226.CrossRefGoogle Scholar
Chandrasekhar, S. 1935a Stellar configurations with degenerate cores. Mon. Not. R. Astron. Soc. 95, 226–260.Google Scholar
Chandrasekhar, S. 1935b Mon. Not. R. Astron. Soc. 170, 405.Google Scholar
Chen, F. F. 1983 Introduction to Plasma Physics and Controlled Fusion. Plenum.Google Scholar
Crouseilles, N., Hervieux, P. A. & Manfredi, G. 2008 Quantum hydrodynamic model for the nonlinear electron dynamics in thin metal films. Phys. Rev. B 78, 155412, 1–11.Google Scholar
El-Taibany, W. F. & Mamun, A. A. 2012 Nonlinear electromagnetic perturbations in a degenerate ultrarelativistic electron–positron plasma. Phys. Rev. E 85, 026406, 1–7.Google Scholar
El-Tantawy, S. A., El-Bedwehy, N. A. & Moslem, W. M. 2011 Nonlinear ion-acoustic structures in dusty plasma with superthermal electrons and positrons. Phys. Plasmas 18, 052113, 1–7.Google Scholar
Ghosh, S., Sarkar, S., Khan, M. & Gupta, M. R. 2002 Ion acoustic shock waves in a collisional dusty plasma. Phys. Plasmas 9, 378–381.Google Scholar
Hussain, S. & Mahmood, S. 2011 Magnetoacoustic solitons in quantum plasma. Phys. Plasmas 18, 082109, 1–5.Google Scholar
Hussain, S., Mahmood, S. & Rehman, A. 2014 Nonlinear magnetosonic waves in dense plasmas with non-relativistic and ultrarelativistic degenerate electrons. Phys. Plasmas 21, 112901, 1–8.Google Scholar
Irfan, M., Ali, S. & Mirza, A. M. 2014 Dust-acoustic solitary and rogue waves in a Thomas–Fermi degenerate dusty plasma. Astrophys. Space Sci. 353, 515–523.Google Scholar
Irfan, M., Ali, S., Mirza, A. M. & Wang, Y. 2015 Modulationally stable envelope solitons in astrophysical magnetoplasmas with degenerate relativistic electrons. J. Plasma Phys. 81, 905810604, 1–14.CrossRefGoogle Scholar
Jehan, N., Mirza, A. M. & Salahuddin, M. 2011 Planar and cylindrical magnetosonic solitary and shock waves in dissipative, hot electron–positron–ion plasma. Phys. Plasmas 18, 052307, 1–11.CrossRefGoogle Scholar
Kakutani, T. & Ono, H. 1969 Weak nonlinear hydromagnetic waves in a cold collision free plasma. J. Phys. Soc. Japan 26, 1305–1318.CrossRefGoogle Scholar
Karpman, V. I. 1975 Nonlinear Waves in Dispersive Medium. Pergamon.Google Scholar
Kourakis, I., Sultana, S. & Verheest, F. 2012 Note on the single-shock solutions of the Korteweg–de Vries–Burgers equation. Astrophys. Space Sci. 338, 245–249.CrossRefGoogle Scholar
Li, S. C. & Han, J. N. 2014 Magnetosonic waves interactions in a spin- $1/2$ degenerate quantum plasma. Phys. Plasmas 21, 032105, 1–8.Google Scholar
Mahmood, S. & Ur-Rehman, H. 2010 Formation of electrostatic solitons, monotonic, and oscillatory shocks in pair-ion plasmas. Phys. Plasmas 17, 072305, 1–6.Google Scholar
Mahmood, S., Sadiq, S. & Haque, Q. 2013 Nonlinear electrostatic excitations in magnetized dense plasmas with nonrelativistic and ultra-relativistic degenerate electrons. Phys. Plasmas 20, 122305, 1–12.Google Scholar
Marklund, M., Eliasson, B. & Shukla, P. K. 2007 Magnetosonic solitons in a fermionic quantum plasma. Phys. Rev. E 76, 067401, 1–4.Google Scholar
Markowich, P. A., Ringhofer, C. A. & Schmeiser, C. 1990 Semiconductor Equations. Springer.CrossRefGoogle Scholar
McKerr, M., Haas, F. & Kourakis, I. 2014 Relativistic theory for localized electrostatic excitations in degenerate electron–ion plasmas. Phys. Rev. E 90, 033112, 1–10.Google Scholar
Moslem, W. M. 2000 Higher-order contributions to ion-acoustic solitary waves in a warm multicomponent plasma with an electron beam. J. Plasma Phys. 63, 139–155.Google Scholar
Moslem, W. M. 2006 Dust-ion-acoustic solitons in a strong magnetic field. Phys. Lett. A 351, 290–295.Google Scholar
Mushtaq, A. & Shah, H. A. 2005a Nonlinear Zakharov Kuznetsov equation for obliquely propagating two-dimensional ion-acoustic solitary waves in a relativistic, rotating magnetized electron–positron–ion plasma. Phys. Plasma 12, 072306, 1–8.Google Scholar
Mushtaq, A. & Shah, H. A. 2005b Effects of positron concentration, ion temperature, and plasma ${\it\beta}$ value on linear and nonlinear two-dimensional magnetosonic waves in electron–positron–ion plasmas. Phys. Plasmas 12, 012301, 1–11.Google Scholar
Mushtaq, A. & Viladimirov, S. V. 2010 Fast and slow magnetosonic waves in two-dimensional spin- $1/2$ quantum plasma. Phys. Plasmas 17, 102310, 1–9.Google Scholar
Nakamura, Y. & Sarma, A. 2001 Observation of ion-acoustic solitary waves in a dusty plasma. Phys. Plasmas 8, 3921–3926.Google Scholar
Rahman, A., Ali, S., Mirza, A. M. & Qamar, A. 2013 Planar and nonplanar ion acoustic shock waves in relativistic degenerate astrophysical electron–positron–ion plasmas. Phys. Plasmas 20, 042305, 1–7.Google Scholar
Rahman, A. & Ali, S. 2014 Solitary and rogue waves in Fermi–Dirac plasmas: relativistic degeneracy effects. Astrophys. Space Sci. 351, 165–172.CrossRefGoogle Scholar
Rahman, A., Kourakis, I. & Qamar, A. 2015b Electrostatic solitary waves in relativistic degenerate electron–positron–ion plasma. IEEE Trans. Plasma Sci. 43, 974–984.Google Scholar
Rahman, A., Mc Kerr, M., El-Taibany, W. F., Kourakis, I. & Qamar, A. 2015a Amplitude modulation of quantum-ion-acoustic wavepackets in electron–positron–ion plasmas: modulational instability, envelope modes, extreme waves. Phys. Plasmas 22, 022305, 1–12.Google Scholar
Salimullah, M., Jamil, M., Shah, H. A. & Murtaza, G. 2009 Jeans instability in a quantum dusty magnetoplasma. Phys. Plasmas 16, 014502, 1–3.Google Scholar
Serbeto, A., Mendonca, J. T., Tsui, K. H. & Bonifacio, R. 2008 Quantum wave kinetics of high-gain free-electron lasers. Phys. Plasmas 15, 013110, 1–5.Google Scholar
Shaikh, D. & Shukla, P. K. 2007 Fluid turbulence in quantum plasmas. Phys. Rev. Lett. 99, 125002, 1–4.CrossRefGoogle ScholarPubMed
Stockman, M. I. 2011 Nanoplasmonics: the physics behind the applications. Phys. Today 64, 39–44.CrossRefGoogle Scholar
Wang, Y., Lu, X. & Eliasson, B. 2013 Modulational instability of spin modified quantum magnetosonic waves in Fermi–Dirac–Pauli plasmas. Phys. Plasmas 20, 112115, 1–7.CrossRefGoogle Scholar
Washimi, H. & Taniuti, T. 1966 Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 17, 996–998.CrossRefGoogle Scholar