Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-09T09:09:40.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetic nulls in interacting dipolar fields

Published online by Cambridge University Press:  03 May 2021

Todd Elder Open the ORCID record for Todd Elder [Opens in a new window]  and
Allen H. Boozer
Todd Elder*
Affiliation:
Department of Applied Physics and Mathematics, Columbia University, New York, NY10027, USA
Allen H. Boozer*
Affiliation:
Department of Applied Physics and Mathematics, Columbia University, New York, NY10027, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The prominence of nulls in reconnection theory is due to the expected singular current density and the indeterminacy of field lines at a magnetic null. Electron inertia changes the implications of both features. Magnetic field lines are distinguishable only when their distance of closest approach exceeds a distance 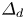$\varDelta _d$. Electron inertia ensures 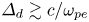$\varDelta _d\gtrsim c/\omega _{pe}$. The lines that lie within a magnetic flux tube of radius 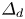$\varDelta _d$ at the place where the field strength 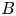$B$ is strongest are fundamentally indistinguishable. If the tube, somewhere along its length, encloses a point where $B=0$ vanishes, then distinguishable lines come no closer to the null than 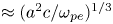$\approx (a^2c/\omega _{pe})^{1/3}$, where 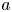$a$ is a characteristic spatial scale of the magnetic field. The behaviour of the magnetic field lines in the presence of nulls is studied for a dipole embedded in a spatially constant magnetic field. In addition to the implications of distinguishability, a constraint on the current density at a null is obtained, and the time required for thin current sheets to arise is derived.

Keywords

astrophysical plasmasplasma properties
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 2 , April 2021 , 905870225
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Boozer, A. H. 2010 Current density and plasma displacement near perturbed rational surfaces. Phys. Plasmas 17, 110707.CrossRefGoogle Scholar
Boozer, A. H. 2012 Magnetic reconnection in space. Phys. Plasmas 19, 092902.CrossRefGoogle Scholar
Boozer, A. 2014 Formation of current sheets in magnetic reconnection. Phys. Plasmas 21, 072907.CrossRefGoogle Scholar
Boozer, A. 2019 a Magnetic reconnection with null and x- points. Phys. Plasmas 26, 122902.CrossRefGoogle Scholar
Boozer, A. H. 2019 b Particle acceleration and fast magnetic reconnection. https://arxiv.org/abs/1902.10860.Google Scholar
Boozer, A. 2020 Magnetic reconnection and thermal equilibration. https://arxiv.org/pdf/2009.14048.pdf.Google Scholar
Boozer, A. & Elder, T. 2020 Simple magnetic reconnection example. https://arxiv.org/pdf/2011.11822.pdf.Google Scholar
Cowley, S. 1973 A qualitative study of the reconnection between the earth's field and interplanetary field of arbitrary orientation. Radio Sci.CrossRefGoogle Scholar
Craig, I. & Effenberger, F. 2014 Current singularities at quasi-separatrix layers and three-dimensional magnetic nulls. Astrophys. J. 795 (2), 129.CrossRefGoogle Scholar
Craig, I. & Fabling, R. 1996 Exact solutions for steady state, spine, and fan magnetic reconnection. Astrophys. J. 462 (2), 969–976.CrossRefGoogle Scholar
Dalla, S. & Browning, P. K. 2005 Particle acceleration at a three-dimensional reconnection site in the solar corona. Astron. Astrophys. 436, 1103–1111.CrossRefGoogle Scholar
Dungey, J. 1961 Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47.CrossRefGoogle Scholar
Dungey, J. 1963 The structure of the exosphere or adventures in velocity space.Google Scholar
Galsgaard, K. & Pontin, D. 2011 Steady state reconnection at a single 3d magnetic null point. Astron. Astrophys. 529.CrossRefGoogle Scholar
Hahm, T. & Kulsrud, R. 1985 Forced magnetic reconnection. Phys. Fluids 28, 2412.CrossRefGoogle Scholar
Hornig, G. & Schindler, K. 1996 Magnetic topology and the problem of its invariant definition. Phys. Plasmas 3, 781.CrossRefGoogle Scholar
Murphy, N., Parnell, C. & Haynes, A. 2015 The appearance, motion, and disappearance of three-dimensional magnetic null points. Phys. Plasmas 22 (10).CrossRefGoogle Scholar
O'Flannagain, A., Maloney, S., Gallagher, P., Browning, P. & Refojo, J. 2018 Three-dimensional magnetic reconnection in a collapsing coronal loop system. Astron. Astrophys. 617.Google Scholar
Olshevsky, V., Lapenta, G. & Markidis, S. 2013 Energetic of kinetic reconnection in a three-dimensional null-point cluster. Phys. Rev. Lett. 111, 045002.CrossRefGoogle Scholar
Pariat, E., Antiochos, S. & DeVore, C. 2009 A model for solar polar jets. Astrophys. J. 691, 61.CrossRefGoogle Scholar
Parnell, C., Smith, J., Neukirch, T. & Priest, E. 1996 The structure of three-dimensional magnetic neutral points. Phys. Plasmas 3, 759.CrossRefGoogle Scholar
Priest, E., Bungey, T. & Titov, V. 1997 The 3d topology and interaction of complex magnetic flux systems. Geophys. Astrophys. Fluid Dyn.CrossRefGoogle Scholar
Stern, D. 1973 A study of the electric field in an open magnetospheric model. J. Geophys. Res.CrossRefGoogle Scholar
Xiao, C. J., Wang, X. G., Pu, Z. Y., Zhao, H., Wang, J. X., Ma, Z. W., Fu, S. Y., Kivelson, M. G., Liu, Z. X., Zong, Q. G., et al. 2006 In situ evidence for the structure of the magnetic null in a 3d reconnection event in the earth's magnetotail. Nature Phys. 2 (7).CrossRefGoogle Scholar