Published online by Cambridge University Press: 15 June 2021
Kinetic-ballooning-mode (KBM) turbulence is studied via gyrokinetic flux-tube simulations in three magnetic equilibria that exhibit small average magnetic shear: the Helically Symmetric eXperiment (HSX), the helical-axis Heliotron-J and a circular tokamak geometry. For HSX, the onset of KBM being the dominant instability at low wavenumber occurs at a critical value of normalized plasma pressure $\beta ^{\rm KBM}_{\rm crit}$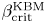 that is an order of magnitude smaller than the magnetohydrodynamic (MHD) ballooning limit $\beta ^{\rm MHD}_{\rm crit}$
that is an order of magnitude smaller than the magnetohydrodynamic (MHD) ballooning limit $\beta ^{\rm MHD}_{\rm crit}$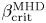 when a strong ion temperature gradient (ITG) is present. However, $\beta ^{\rm KBM}_{\rm crit}$
when a strong ion temperature gradient (ITG) is present. However, $\beta ^{\rm KBM}_{\rm crit}$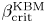 increases and approaches the MHD ballooning limit as the ITG tends to zero. For these configurations, $\beta ^{\rm KBM}_{\rm crit}$
increases and approaches the MHD ballooning limit as the ITG tends to zero. For these configurations, $\beta ^{\rm KBM}_{\rm crit}$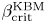 also increases as the magnitude of the average magnetic shear increases, regardless of the sign of the normalized magnetic shear. Simulations of Heliotron-J and a circular axisymmetric geometry display behaviour similar to HSX with respect to $\beta ^{\rm KBM}_{\rm crit}$
also increases as the magnitude of the average magnetic shear increases, regardless of the sign of the normalized magnetic shear. Simulations of Heliotron-J and a circular axisymmetric geometry display behaviour similar to HSX with respect to $\beta ^{\rm KBM}_{\rm crit}$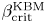 . Despite large KBM growth rates at long wavelengths in HSX, saturation of KBM turbulence with $\beta > \beta _{\rm crit}^{\rm KBM}$
. Despite large KBM growth rates at long wavelengths in HSX, saturation of KBM turbulence with $\beta > \beta _{\rm crit}^{\rm KBM}$ is achievable in HSX and results in lower heat transport relative to the electrostatic limit by a factor of roughly five. Nonlinear simulations also show that KBM transport dominates the dynamics when KBMs are destabilized linearly, even if KBM growth rates are subdominant to ITG growth rates.
is achievable in HSX and results in lower heat transport relative to the electrostatic limit by a factor of roughly five. Nonlinear simulations also show that KBM transport dominates the dynamics when KBMs are destabilized linearly, even if KBM growth rates are subdominant to ITG growth rates.