Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T14:16:09.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved multispecies Dougherty collisions

Published online by Cambridge University Press:  12 May 2022

Manaure Francisquez Open the ORCID record for Manaure Francisquez [Opens in a new window] ,
James Juno Open the ORCID record for James Juno [Opens in a new window] ,
Ammar Hakim ,
Gregory W. Hammett Open the ORCID record for Gregory W. Hammett [Opens in a new window]  and
Darin R. Ernst Open the ORCID record for Darin R. Ernst [Opens in a new window]
Manaure Francisquez*
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08543, USA MIT Plasma Science and Fusion Center, Cambridge, MA 02139, USA
James Juno
Affiliation:
Department of Physics & Astronomy, University of Iowa, Iowa City, IA 52242, USA
Ammar Hakim
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08543, USA
Gregory W. Hammett
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ 08543, USA
Darin R. Ernst
Affiliation:
MIT Plasma Science and Fusion Center, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

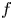The Dougherty model Fokker–Planck operator is extended to describe nonlinear full-$f$ ( f is the distribution function) collisions between multiple species in plasmas. Simple relations for cross-species primitive moments are developed which obey conservation laws, and reproduce familiar velocity and temperature relaxation rates. This treatment of multispecies Dougherty collisions, valid for arbitrary mass ratios, avoids unphysical temperatures and satisfies the $H$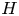-theorem (H is related to the entropy) unlike an analogous Bhatnagar–Gross–Krook operator. Formulas for both a Cartesian velocity space and a gyroaveraged operator are provided for use in Vlasov as well as long-wavelength gyrokinetic models. We present an algorithm for the discontinuous Galerkin discretization of this operator, and provide results from relaxation and Landau damping benchmarks.

Keywords

plasma dynamicsplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 3 , June 2022 , 905880303
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abel, I.G., Barnes, M., Cowley, S.C., Dorland, W. & Schekochihin, A.A. 2008 Linearized model Fokker–Planck collision operators for gyrokinetic simulations. I. Theory. Phys. Plasmas 15 (12), 122509.CrossRefGoogle Scholar
Anderson, M.W. & O'Neil, T.M. 2007 Eigenfunctions and eigenvalues of the Dougherty collision operator. Phys. Plasmas 14 (5), 052103.CrossRefGoogle Scholar
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.CrossRefGoogle Scholar
Cockburn, B. & Shu, C.-W. 1998 The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35 (6), 2440–2463.CrossRefGoogle Scholar
Dougherty, J.P. 1964 Model Fokker–Planck equation for a plasma and its solution. Phys. Fluids 7 (11), 1788–1799.CrossRefGoogle Scholar
Dougherty, J.P. & Watson, S.R. 1967 Model Fokker–Planck equations: Part 2. The equation for a multicomponent plasma. J. Plasma Phys. 1 (3), 317–326.CrossRefGoogle Scholar
Estève, D., Garbet, X., Sarazin, Y., Grandgirard, V., Cartier-Michaud, T., Dif-Pradalier, G., Ghendrih, P., Latu, G. & Norscini, C. 2015 A multi-species collisional operator for full-F gyrokinetics. Phys. Plasmas 22 (12), 122506.CrossRefGoogle Scholar
Francisquez, M., Bernard, T.N., Mandell, N.R., Hammett, G.W. & Hakim, A. 2020 Conservative discontinuous Galerkin scheme of a gyro-averaged Dougherty collision operator. Nucl. Fusion 60 (9), 096021.CrossRefGoogle Scholar
Frei, B.J., Ball, J., Hoffmann, A.C.D., Jorge, R., Ricci, P. & Stenger, L. 2021 Development of advanced linearized gyrokinetic collision operators using a moment approach. J. Plasma Phys. 87, 905870501.CrossRefGoogle Scholar
Gkeyll 2020 The Gkeyll 2.0 Code: documentation home. http://gkeyll.readthedocs.io.Google Scholar
Greene, J.M. 1973 Improved Bhatnagar–Gross–Krook model of electron-ion collisions. Phys. Fluids 16 (11), 2022–2023.CrossRefGoogle Scholar
Haack, J.R., Hauck, C.D. & Murillo, M.S. 2017 A conservative, entropic multispecies BGK model. J. Stat. Phys. 168 (4), 826–856.CrossRefGoogle Scholar
Hager, R., Yoon, E.S., Ku, S., D'Azevedo, E.F., Worley, P.H. & Chang, C.S. 2016 A fully non-linear multi-species Fokker–Planck–Landau collision operator for simulation of fusion plasma. J. Comput. Phys. 315, 644–660.CrossRefGoogle Scholar
Hakim, A., Francisquez, M., Juno, J. & Hammett, G.W. 2020 Conservative discontinuous Galerkin schemes for nonlinear Dougherty–Fokker–Planck collision operators. J. Plasma Phys. 86 (4), 905860403.CrossRefGoogle Scholar
Hakim, A. & Juno, J. 2020 Alias-free, matrix-free, and quadrature-free discontinuous Galerkin algorithms for (plasma) kinetic equations. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC ’20, vol. 73. IEEE.CrossRefGoogle Scholar
Hesthaven, J.S. & Warburton, T. 2007 Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer.Google Scholar
Hinton, F.L. & Hazeltine, R.D. 1976 Theory of plasma transport in toroidal confinement systems. Rev. Mod. Phys. 48, 239–308.CrossRefGoogle Scholar
Hirvijoki, E., Brizard, A.J. & Pfefferlé, D. 2017 Differential formulation of the gyrokinetic Landau operator. J. Plasma Phys. 83 (1), 595830102.CrossRefGoogle Scholar
Huba, J.D. 2013 NRL Plasma Formulary, Supported by the Office of Naval Research. Naval Research Laboratory.Google Scholar
Jorge, R., Ricci, P., Brunner, S., Gamba, S., Konovets, V., Loureiro, N.F., Perrone, L.M. & Teixeira, N. 2019 Linear theory of electron-plasma waves at arbitrary collisionality. J. Plasma Phys. 85 (2), 905850211.CrossRefGoogle Scholar
Jorge, R., Ricci, P. & Loureiro, N.F. 2018 Theory of the drift-wave instability at arbitrary collisionality. Phys. Rev. Lett. 121, 165001.CrossRefGoogle ScholarPubMed
Juno, J., Hakim, A., TenBarge, J., Shi, E. & Dorland, W. 2018 Discontinuous Galerkin algorithms for fully kinetic plasmas. J. Comput. Phys. 353, 110–147.CrossRefGoogle Scholar
Kolesnikov, R.A., Wang, W.X. & Hinton, F.L. 2010 Unlike-particle collision operator for gyrokinetic particle simulations. J. Comput. Phys. 229 (15), 5564–5572.CrossRefGoogle Scholar
van Leer, B. & Lo, M. 2007 A discontinuous Galerkin method for diffusion based on recovery. In 18th AIAA Computational Fluid Dynamics Conference, AIAA 2007-4083, pp. 1–12. American Institute of Aeronautics.CrossRefGoogle Scholar
van Leer, B. & Nomura, S. 2005 Discontinuous Galerkin for diffusion. In 17th AIAA Computational Fluid Dynamics Conference, AIAA 2005-5109, pp. 1–30. American Institute of Aeronautics.CrossRefGoogle Scholar
Li, B. & Ernst, D.R. 2011 Gyrokinetic Fokker–Planck collision operator. Phys. Rev. Lett. 106 (19), 195002.CrossRefGoogle ScholarPubMed
Mandell, N.R., Hakim, A., Hammett, G.W. & Francisquez, M. 2020 Electromagnetic full-$f$ gyrokinetics in the tokamak edge with discontinuous Galerkin methods. J. Plasma Phys. 86, 905860109. arXiv:1908.05653CrossRefGoogle Scholar
Morse, T.F. 1963 Energy and momentum exchange between nonequipartition gases. Phys. Fluids 6 (10), 1420–1427.CrossRefGoogle Scholar
Morse, T.F. 1964 Kinetic model equations for a gas mixture. Phys. Fluids 7 (12), 2012–2013.CrossRefGoogle Scholar
Ong, R.S.B. & Yu, M.Y. 1970 The effect of velocity space diffusion on the universal instability in a plasma. J. Plasma Phys. 4 (4), 729–738.CrossRefGoogle Scholar
Ong, R.S.B. & Yu, M.Y. 1973 The effect of temperature perturbations on ion-acoustic and drift waves in a weakly collisional plasma. Plasma Phys. 15 (7), 659–668.CrossRefGoogle Scholar
Pan, Q. & Ernst, D.R. 2019 Gyrokinetic Landau collision operator in conservative form. Phys. Rev. E 99, 023201.CrossRefGoogle ScholarPubMed
Pan, Q., Ernst, D.R. & Crandall, P. 2020 First implementation of gyrokinetic exact linearized Landau collision operator and comparison with models. Phys. Plasmas 27, 042307.CrossRefGoogle Scholar
Pan, Q., Ernst, D.R. & Hatch, D. 2021 Importance of gyrokinetic exact Fokker–Planck collisions in fusion plasma turbulence. Phys. Rev. E 103, L051202.CrossRefGoogle ScholarPubMed
Pan, Q., Told, D., Shi, E.L., Hammett, G.W. & Jenko, F. 2018 Full-$f$ version of GENE for turbulence in open-field-line systems. Phys. Plasmas 25 (6), 062303.CrossRefGoogle Scholar
Pezzi, O., Valentini, F. & Veltri, P. 2015 Collisional relaxation: Landau versus Dougherty operator. J. Plasma Phys. 81 (1), 305810107.CrossRefGoogle Scholar
Pusztai, I., Juno, J., Brandenburg, A., TenBarge, J.M., Hakim, A., Francisquez, M. & Sundström, A. 2020 Dynamo in weakly collisional nonmagnetized plasmas impeded by Landau damping of magnetic fields. Phys. Rev. Lett. 124, 255102.CrossRefGoogle ScholarPubMed
Rosenbluth, M.N., MacDonald, W.M. & Judd, D.L. 1957 Fokker–Planck equation for an inverse-square force. Phys. Rev. 107 (1), 1–6.CrossRefGoogle Scholar
Shi, E.L., Hammett, G.W., Stoltzfus-Dueck, T. & Hakim, A. 2019 Full-$f$ gyrokinetic simulation of turbulence in a helical open-field-line plasma. Phys. Plasmas 26 (1), 012307.CrossRefGoogle Scholar
Sugama, H., Matsuoka, S., Satake, S., Nunami, M. & Watanabe, T.-H. 2019 Improved linearized model collision operator for the highly collisional regime. Phys. Plasmas 26 (10), 102108.CrossRefGoogle Scholar
Sugama, H., Watanabe, T.-H. & Nunami, M. 2009 Linearized model collision operators for multiple ion species plasmas and gyrokinetic entropy balance equations. Phys. Plasmas 16 (11), 112503.CrossRefGoogle Scholar
Ulbl, P., Michels, D. & Jenko, F. 2021 Implementation and verification of a conservative, multi-species, gyro-averaged, full-f, Lenard–Bernstein/Dougherty collision operator in the gyrokinetic code GENE-X. Contrib. Plasma Phys. e202100180.Google Scholar