Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T13:22:04.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized expressions for momentum and energy losses of charged particle beams in non-Maxwellian multi-species plasmas and spherical symmetry

Published online by Cambridge University Press:  13 March 2009

S. Cuperman ,
I. Weiss  and
M. Dryer
S. Cuperman
Affiliation:
Department of Physics and Astronomy, Tel Aviv University, Tel Aviv, 69978, Israel
I. Weiss
Affiliation:
Department of Physics and Astronomy, Tel Aviv University, Tel Aviv, 69978, Israel
M. Dryer
Affiliation:
Space Environmental Laboratory, ERL, NOAA, Boulder, Colorado, 80303, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Generalized expressions for the rates of change of the momentum, energy and thermal anisotropy of fast, charged particle beams interacting with non-Maxwellian multi-species plasmas are derived. The results hold for the case of spherically symmetric systems and, therefore, are relevant for inertial confinement fusion schemes driven by fast charged particle beams and for various astro-physical situations. The calculations are based on the Fokker-Planckformalism. The effects connected with the departures from the Maxwellian distribution functions are expressed in terms of their fifth moments, 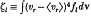, which reflect the role of the non-Maxwellian tails. The familiar stopping power expression holding for Maxwellian targets is recovered as a particular case.

Type
Research Article
Information
Journal of Plasma Physics , Volume 28 , Issue 3 , December 1982 , pp. 445 - 457
Copyright
Copyright © Cambridge University Press 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Braginskii, S. I. 1965 Reviews of Plasma Physics, vol. 1 (ed. Leontovich, M. A.). Consultants Bureau.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases. Cambridge University Press.Google Scholar
Clauser, M. J. 1975 Phys. Rev. Lett. 35, 848.CrossRefGoogle Scholar
Cuperman, S. & Levush, B. 1981 Nucl. Fusion, 8, 1020.CrossRefGoogle Scholar
Cuperman, S., Weiss, I. & Dryer, M. 1980 Ap. J. 239, 345.CrossRefGoogle Scholar
Cuperman, S., Weiss, I. & Dryer, M. 1982 Tel-Aviv University Report TAUP 1005–82.Google Scholar
Humphries, S. 1981 Nucl. Fusion, 20, 1549.CrossRefGoogle Scholar
Larson, R. B. 1970 MNRAS, 147, 323.Google Scholar
Rosenbluth, M., MacDonald, W. M. & Judd, D. L. 1957 Phys. Rev. 107, 1.CrossRefGoogle Scholar
Shearer, J. W. 1975 Nucl. Fusion, 15, 952.CrossRefGoogle Scholar
Sivukhin, D. V. 1966 Reviews of Plasma Physics, vol. 1 (ed. Leontovich, M. A.). Consultants Bureau.Google Scholar
Spitzer, L. 1956 Physics of Fully Ionized Gases. Interscience.Google Scholar
Winterberg, F. 1975 Plasma Phys. 12, 69.CrossRefGoogle Scholar