Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-07T15:24:56.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Four-dimensional equations for the study of electromagnetic plasma turbulence in a drift kinetic limit

Published online by Cambridge University Press:  28 February 2022

Evgeny A. Gorbunov Open the ORCID record for Evgeny A. Gorbunov [Opens in a new window]  and
Bogdan Teaca Open the ORCID record for Bogdan Teaca [Opens in a new window]
Evgeny A. Gorbunov*
Affiliation:
Coventry University, CoventryCV1 5FB, United Kingdom
Bogdan Teaca*
Affiliation:
University of Craiova, 13 A.I. Cuza Street, 200585Craiova, Romania
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a magnetised plasma in a straight magnetic guide field, we derive a set of four-dimensional kinetic equations, which can capture electromagnetic turbulence in the drift kinetic limit. To do so, we start from the gyrokinetic equations, employ a Laguerre decomposition in the perpendicular velocity direction, retaining only the dominant gyroaverage contributions and only the first two Laguerre moments that source the electromagnetic fluctuations. The model conserves free energy, and can describe electromagnetic turbulence for a plasma at the transition between fluid and gyrokinetic regimes ($k_\perp \rho _i\approx 1$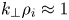 range of scales), as dominant finite-Larmor-radius (FLR) effects are considered. In addition to the three dimensions in positions space, we retain the parallel velocity dependence, which we describe via a Hermite representation. Employing this system, but without any other physics-based assumptions for the plasma species that can bias results, will allow us to investigate how fluid effects transition into the kinetic range, and analyse the interplay between spatial and velocity space mixing for electromagnetic plasma turbulence.

Keywords

Astrophysical plasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 905880117
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adkins, T. & Schekochihin, A.A. 2018 A solvable model of Vlasov–kinetic plasma turbulence in Fourier–Hermite phase space. J. Plasma Phys. 84 (1), 905840107.CrossRefGoogle Scholar
Alexandrova, O., Carbone, V., Veltri, P. & Sorriso-Valvo, L. 2008 Small-scale energy cascade of the solar wind turbulence. Astrophys. J. 674, 1153.CrossRefGoogle Scholar
Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S.J. & Robert, P. 2009 Universality of solar-wind turbulent spectrum from MHD to electron scales. Phys. Rev. Lett. 103, 165003.CrossRefGoogle ScholarPubMed
Beer, M.A. & Hammett, G.W. 1996 Toroidal gyrofluid equations for simulations of tokamak turbulence. Phys. Plasmas 3, 4046.CrossRefGoogle Scholar
Bhattacharjee, A., Ng, C.S. & Spangler, S.R. 1998 Weakly compressible magnetohydrodynamic turbulence in the solar wind and the interstellar medium. Astrophys. J. 494, 409.CrossRefGoogle Scholar
Brizard, A. 1992 Nonlinear gyrofluid description of turbulent magnetized plasmas. Phys. Fluids B 4 (5), 1213–1228.CrossRefGoogle Scholar
Cerri, S.S., Kunz, M.W. & Califano, F. 2018 Dual phase-space cascades in 3D hybrid-Vlasov-Maxwell turbulence. Astrophys. J. Lett. 856, L13.CrossRefGoogle Scholar
Chandran, B., Quataert, E., Howes, G.G., Hollweg, J.V. & Dorland, W. 2009 The turbulent heating rate in strong magnetohydrodynamic turbulence with nonzero cross helicity. Astrophys. J. 701, 652.CrossRefGoogle Scholar
Dorland, W. & Hammett, G.W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B 5 (3), 812–835.CrossRefGoogle Scholar
Duan, D., Bowen, T.A., Chen, C.H.K., Mallet, A., He, J., Bale, S.D., Vech, D., Kasper, J.C., Pulupa, M., Bonnell, J.W., et al. 2020 The radial dependence of proton-scale magnetic spectral break in slow solar wind during PSP encounter 2. Astrophys. J. Suppl. 246 (2), 55.CrossRefGoogle Scholar
Duan, D., He, J., Bowen, T.A., Woodham, L.D., Wang, T., Chen, C.H.K., Mallet, A. & Bale, S.D. 2021 Anisotropy of solar wind turbulence in the inner heliosphere at kinetic scales: PSP observations. Astrophys. J. Lett. 915 (1), L8.CrossRefGoogle Scholar
Eyink, G.L. 2018 Cascades and dissipative anomalies in nearly collisionless plasma turbulence. Phys. Rev. X 8, 041020.Google Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. 2. Strong Alfvenic turbulence. Astrophys. J. 438, 763.CrossRefGoogle Scholar
Grošelj, D., Chen, C.H.K., Mallet, A., Samtaney, R., Schneider, K. & Jenko, F. 2019 Kinetic turbulence in astrophysical plasmas: waves and/or structures? Phys. Rev. X 9 (3), 031037.Google Scholar
Hatch, D.R., Jenko, F., Bratanov, V. & Navarro, A.B. 2014 Phase space scales of free energy dissipation in gradient-driven gyrokinetic turbulence. J. Plasma Phys. 80 (4), 531–551.CrossRefGoogle Scholar
Howes, G.G., Cowley, S.C., Dorland, W., Hammett, G.W., Quataert, E. & Schekochihin, A.A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651, 590.CrossRefGoogle Scholar
Howes, G.G., Dorland, W., Cowley, S.C., Hammett, G.W., Quataert, E., Schekochihin, A.A. & Tatsuno, T. 2008 Kinetic simulations of magnetized turbulence in astrophysical plasmas. Phys. Rev. Lett. 100, 65004.CrossRefGoogle ScholarPubMed
Howes, G.G., Tenbarge, J.M., Dorland, W., Quataert, E., Schekochihin, A.A., Numata, R. & Tatsuno, T. 2011 Gyrokinetic simulations of solar wind turbulence from ion to electron scales. Phys. Rev. Lett. 107, 35004.CrossRefGoogle ScholarPubMed
Kawazura, Y., Barnes, M. & Schekochihin, A.A. 2019 Thermal disequilibration of ions and electrons by collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116 (3), 771–776.CrossRefGoogle ScholarPubMed
Kunz, M., Abel, I., Klein, K. & Schekochihin, A. 2018 Astrophysical gyrokinetics: turbulence in pressure-anisotropic plasmas at ion scales and beyond. J. Plasma Phys. 84 (2), 715840201.CrossRefGoogle Scholar
Loureiro, N., Dorland, W., Fazendeiro, L., Kanekar, A., Mallet, A., Vilelas, M. & Zocco, A. 2016 Viriato: a Fourier–Hermite spectral code for strongly magnetized fluid–kinetic plasma dynamics. Comput. Phys. Commun. 206, 45–63.CrossRefGoogle Scholar
Mandell, N., Dorland, W. & Landreman, M. 2018 Laguerre–Hermite pseudo-spectral velocity formulation of gyrokinetics. J. Plasma Phys. 84 (1), 905840108.CrossRefGoogle Scholar
Meyrand, R., Kanekar, A., Dorland, W. & Schekochihin, A.A. 2019 Fluidization of collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116 (4), 1185–1194.CrossRefGoogle ScholarPubMed
Meyrand, R., Squire, J., Schekochihin, A. & Dorland, W. 2021 On the violation of the zeroth law of turbulence in space plasmas. J. Plasma Phys. 87 (3), 535870301.CrossRefGoogle Scholar
Navarro, A.B., Teaca, B., Told, D., Groselj, D., Crandall, P. & Jenko, F. 2016 Structure of plasma heating in gyrokinetic Alfvénic turbulence. Phys. Rev. Lett. 117 (24), 245101.CrossRefGoogle ScholarPubMed
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Plunk, G.G., Quataert, E. & Tatsuno, T. 2008 Gyrokinetic turbulence: a nonlinear route to dissipation through phase space. Plasma Phys. Control. Fusion 50, 4024.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182 (1), 310–377.CrossRefGoogle Scholar
Schekochihin, A.A., Parker, J.T., Highcock, E.G., Dellar, P.J., Dorland, W. & Hammett, G.W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82 (2), 905820212.CrossRefGoogle Scholar
Servidio, S., Valentini, F., Califano, F. & Veltri, P. 2012 Local kinetic effects in two-dimensional plasma turbulence. Phys. Rev. Lett. 108, 045001.CrossRefGoogle ScholarPubMed
Snyder, P.B. & Hammett, G.W. 2001 A Landau fluid model for electromagnetic plasma microturbulence. Phys. Plasmas 8 (7), 3199–3216.CrossRefGoogle Scholar
Snyder, P.B., Hammett, G.W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4 (11), 3974–3985.CrossRefGoogle Scholar
Tatsuno, T., Dorland, W., Schekochihin, A.A., Plunk, G.G., Barnes, M., Cowley, S.C. & Howes, G.G. 2009 Nonlinear phase mixing and phase-space cascade of entropy in gyrokinetic plasma turbulence. Phys. Rev. Lett. 103, 15003.CrossRefGoogle ScholarPubMed
Teaca, B., Gorbunov, E.A., Told, D., Bañón Navarro, A. & Jenko, F. 2021 Sub-grid-scale effects in magnetised plasma turbulence. J. Plasma Phys. 87 (2), 905870209.CrossRefGoogle Scholar
Teaca, B., Jenko, F. & Told, D. 2017 Gyrokinetic turbulence: between idealized estimates and a detailed analysis of nonlinear energy transfers. New J. Phys. 19, 045001.CrossRefGoogle Scholar
Teaca, B., Navarro, A.B. & Jenko, F. 2014 The energetic coupling of scales in gyrokinetic plasma turbulence. Phys. Plasmas 21, 072308.CrossRefGoogle Scholar
Teaca, B., Navarro, A.B., Jenko, F., Brunner, S. & Villard, L. 2012 Locality and universality in gyrokinetic turbulence. Phys. Rev. Lett. 109, 235003.CrossRefGoogle ScholarPubMed
Teaca, B., Navarro, A.B., Told, D., Görler, T., Plunk, G., Hatch, D.R. & Jenko, F. 2019 A look at phase space intermittency in magnetized plasma turbulence. Astrophys. J. 886, 65.CrossRefGoogle Scholar
Tenbarge, J.M. & Howes, G.G. 2013 Current sheets and collisionless damping in kinetic plasma turbulence. Astrophys. J. Lett. 771, L27.CrossRefGoogle Scholar
Told, D., Jenko, F., TenBarge, J.M., Howes, G.G. & Hammett, G.W. 2015 Multiscale nature of the dissipation range in gyrokinetic simulations of Alfvénic turbulence. Phys. Rev. Lett. 115, 025003.CrossRefGoogle ScholarPubMed
Vech, D., Kasper, J.C., Klein, K.G., Huang, J., Stevens, M.L., Chen, C.H.K., Case, A.W., Korreck, K., Bale, S.D., Bowen, T.A., et al. 2020 Kinetic-scale spectral features of cross helicity and residual energy in the inner heliosphere. Astrophys. J. Suppl. 246 (2), 52.CrossRefGoogle Scholar
Wan, M., Matthaeus, W.H., Karimabadi, H., Roytershteyn, V., Shay, M., Wu, P., Daughton, W., Loring, B. & Chapman, S.C. 2012 Intermittent dissipation at kinetic scales in collisionless plasma turbulence. Phys. Rev. Lett. 109, 195001.CrossRefGoogle ScholarPubMed
Weidl, M.S., Jenko, F., Teaca, B. & Schlickeiser, R. 2015 Cosmic-ray pitch-angle scattering in imbalanced mhd turbulence simulations. Astrophys. J. 811, 8.CrossRefGoogle Scholar
Zhao, L.-L., Zank, G.P., Adhikari, L., Nakanotani, M., Telloni, D. & Carbone, F. 2020 Spectral features in field-aligned solar wind turbulence from parker solar probe observations. Astrophys. J. 898 (2), 113.CrossRefGoogle Scholar
Zhdankin, V., Boldyrev, S., Mason, J. & Perez, J.C. 2012 Magnetic discontinuities in magnetohydrodynamic turbulence and in the solar wind. Phys. Rev. Lett. 108, 175004.CrossRefGoogle ScholarPubMed
Zhou, Y., Matthaeus, W.H. & Dmitruk, P. 2004 Colloquium: magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev. Mod. Phys. 76, 1015.CrossRefGoogle Scholar
Zocco, A. & Schekochihin, A.A. 2011 Reduced fluid–kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18 (10), 102309.CrossRefGoogle Scholar