Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T14:02:35.898Z Has data issue: false hasContentIssue false
  • English
  • Français

The external kink mode in diverted tokamaks

Part of: PLA Tribute to V D Shafranov: 1929-2014 Focus on Fusion

Published online by Cambridge University Press:  16 June 2016

A. D. Turnbull ,
J. M. Hanson ,
F. Turco ,
N. M. Ferraro ,
M. J. Lanctot ,
L. L. Lao ,
E. J. Strait ,
P. Piovesan  and
P. Martin
A. D. Turnbull*
Affiliation:
General Atomics Inc, San Diego, California, USA
J. M. Hanson
Affiliation:
Columbia University, New York, USA
F. Turco
Affiliation:
Columbia University, New York, USA
N. M. Ferraro
Affiliation:
Princeton Plasma Physics Laboratory, Princeton, NJ, USA
M. J. Lanctot
Affiliation:
General Atomics Inc, San Diego, California, USA
L. L. Lao
Affiliation:
General Atomics Inc, San Diego, California, USA
E. J. Strait
Affiliation:
General Atomics Inc, San Diego, California, USA
P. Piovesan
Affiliation:
Consorzio RFX, Padova, Italy
P. Martin
Affiliation:
Consorzio RFX, Padova, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An explanation is provided for the disruptive instability in diverted tokamaks when the safety factor $q$ at the 95 % poloidal flux surface, 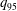$q_{95}$ , is driven below 2.0. The instability is a resistive kink counterpart to the current-driven ideal mode that traditionally explained the corresponding disruption in limited cross-sections (Shafranov, Sov. Phys. Tech. Phys., vol. 15, 1970, p. 175) when 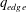$q_{edge}$ , the safety factor at the outermost closed flux surface, lies just below a rational value 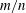$m/n$ . Experimentally, external kink modes are observed in limiter configurations as the current in a tokamak is ramped up and 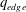$q_{edge}$ decreases through successive rational surfaces. For $q_{edge}<2$ , the instability is always encountered and is highly disruptive. However, diverted plasmas, in which 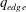$q_{edge}$ is formally infinite in the magnetohydrodynamic (MHD) model, have presented a longstanding difficulty since the theory would predict stability, yet, the disruptive limit occurs in practice when 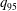$q_{95}$ , reaches 2. It is shown from numerical calculations that a resistive kink mode is linearly destabilized by the rapidly increasing resistivity at the plasma edge when 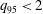$q_{95}<2$ , but 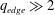$q_{edge}\gg 2$ . The resistive kink behaves much like the ideal kink with predominantly kink or interchange parity and no real sign of a tearing component. However, the growth rates scale with a fractional power of the resistivity near the 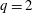$q=2$ surface. The results have a direct bearing on the conventional edge cutoff procedures used in most ideal MHD codes, as well as implications for ITER and for future reactor options.

Type
Research Article
Information
Journal of Plasma Physics , Volume 82 , Issue 3 , June 2016 , 515820301
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bernard, L. C., Helton, F. J. & Moore, R. W. 1981 GATO: an MHD stability code for axisymmetric plasmas with internal separatrices. Comput. Phys. Commun. 24, 377–380.Google Scholar
Bol, K., Okabayashi, M. & Fonck, R. 1985 The poloidal divertor experiment (PDX) and the princeton beta experiment (PBX). Nucl. Fusion 25, 1149–1153.Google Scholar
Bondeson, A., Vlad, G. & Lutjens, H. 1992 Resistive toroidal stability of internal kink modes in circular and shaped tokamas. Phys. Fluids B4, 1889–1900.CrossRefGoogle Scholar
Bussac, M. N., Edery, D., Pellat, R. & Soule, J. L. 1976 Internal kink modes in toroidal plasmas with circular cross sections. Phys. Rev. Lett. 35, 1638–1641.Google Scholar
Charlton, L. A., Carreras, B. A., Holmes, J. A. & Lynch, V. E. 1988 Tokamak $m=1$ magnetohydrodynamic calculations in toroidal geometry using a full set of nonlinear resistive magnetohydrodynamic equations. Phys. Fluids 31, 347–358.Google Scholar
Chu, M. S. & Okabayashi, M. 2010 Stabilization of the external kink and the resistive wall mode. Plasma Phys. Control. Fusion 52, 123001.CrossRefGoogle Scholar
Coppi, B., Galvao, R., Pellat, R., Rosenbluth, M. N. & Rutherford, P. H. 1976 Resistive internal kink modes. Sov. J. Plasma Phys. 2, 533–535.Google Scholar
Degtyarev, L., Martynov, A., Medvedev, S., Troyon, F., Villard, L. & Gruber, R. The KINX ideal MHD stability code for axisymmetric plasmas with separatrix. Comput. Phys. Commun. 103, 10–27.Google Scholar
Eldon, D., Boivin, R. L., Groebner, R. J., Osborne, T. H., Snyder, P. B., Turnbull, A. D., Tynan, G. R., Boedo, J. A., Burrell, K. H., Kolemen, E. et al. 2015 Investigation of peeling-ballooning stability prior to transient outbursts accompanying transitions out of $H$ -mode in DIII-D. Phys. Plasmas 22, 052109.Google Scholar
Evans, T. E., Moyer, R. A., Burrell, K. H., Fenstermacher, M. E., Joseph, I., Leonard, A. W., Osborne, T. H., Porter, G. D., Schaffer, M. J., Snyder, P. B. et al. 2006 Edge stability and transport control with resonant magnetic perturbations in collisionless tokamak plasmas. Nat. Phys. 2, 419–423.CrossRefGoogle Scholar
Ferraro, N. M., Jardin, S. C. & Snyder, P. B. 2010 Ideal and resistive edge stability calculations with M3D-C $^{1}$ . Phys. Plasmas 17, 102508.CrossRefGoogle Scholar
Freidberg, J. P. 1987 Ideal Magnetohydrodynamics. Plenum.Google Scholar
Garofalo, A. M., Turnbull, A. D., Austin, M. E., Bialek, J., Chu, M. S., Comer, K. J., Fredrickson, E. D., Groebner, R. J., La Haye, R. J., Lao, L. L. et al. 1999 Direct observation of the resistive wall mode in a tokamak and its interaction with plasma rotation. Phys. Rev. Lett. 82, 3811–3814.CrossRefGoogle Scholar
Glasser, A. H., Greene, J. M. & Johnson, J. L. 1975 Resistive instabilities in general toroidal plasma configurations. Phys. Fluids 18, 875–888.Google Scholar
Glasser, A. H. 1997 Determination of free boundary ideal MHD stability with DCON and VACUUM. Bull. Am. Phys. Soc. 42, 1848. See also Glasser A. H. 2014 The direct criterion of Newcomb for the stability of an axisymmetric toroidal plasma (unpublished report).Google Scholar
Gruber, R., Troyon, F., Rousset, S., Kerner, W. & Bernard, L. C. 1981 ERATO stability code. Comput. Phys. Commun. 21, 323–371.Google Scholar
Hanson, J. M., Bialek, J. M., Baruzzo, M., Bolzonella, T., Hyatt, A. W., Jackson, G. L., King, J., La Haye, R. J., Lanctot, M. J., Marrelli, L. et al. 2014 Feedback-assisted extension of the tokamak operating space to low safety factor. Phys. Plasmas 21, 072107.Google Scholar
Hanson, J. M., Bialek, J., Turco, F., King, J., Navratil, G. A., Strait, E. J. & Turnbull, A. D. 2016 Validation of conducting wall models using magnetic measurements. Nucl. Fusion (submitted).CrossRefGoogle Scholar
Hastie, R. J., Hender, T. C., Carreras, B. A., Charlton, L. A. & Holmes, J. A. 1987 Stability of ideal and resistive internal kink modes in toroidal geometry. Phys. Fluids 30, 1756–1766.Google Scholar
Hender, T. C., Gryaznevich, M., Liu, Y. Q., Bigi, M., Buttery, R. J., Bondeson, A., Gimblett, C. G., Howell, D. F., Pinches, S. D., de Baar, M. et al. 2014 Resistive wall mode studies in JET. In Proceedings of 20th International Fusion Energy Conference Villamora, Portugal, October 2004, EX/P2-22, IAEA.Google Scholar
Hugon, M., Balet, B., Christiansen, J. P., Edwards, A., Fishpool, G., Gimblett, C., Gottardi, G. N., Hastie, R. J., Lomas, P., van Milligen, B. et al. 1991 Current Rise Studies (ed. Bachmann, P. & Robinson, D. C.), pp. 41–43. European Physical Society.Google Scholar
Huysmans, G. T. A., Goedbloed, J. P. & Kerner, W. 1993 Free boundary resistive modes in tokamaks. Phys. Plasmas B5, 1545–1558.Google Scholar
Lao, L. L., Ferron, J. R., Groebner, R. J., Howl, W., St. John, H., Strait, E. J. & Taylor, T. S. 1990 Equilibrium analysis of current profiles in tokamaks. Nucl. Fusion 30, 1035–1049.Google Scholar
Lazarus, E. A., Navratil, G. A., Greenfield, C. M., Strait, E. J., Turnbull, A. D. & Taylor, T. S. 1997 Higher fusion power gain with profile control in DIII-D tokamak plasmas. Nucl. Fusion 37, 7–12.Google Scholar
Lutjens, H., Bondeson, A. & Sauter, O. 1996 The CHEASE code for toroidal MHD equilibria. Comput. Phys. Commun. 97, 219–260.CrossRefGoogle Scholar
Martin, P., Apolloni, L., Puiatti, M. E., Adamek, J., Agostini, M., Alfier, A., Annibaldi, S. V., Antoni, V., Auriemma, F., Barana, O. et al. 2009 Overview of RFX-mod results. Nucl. Fusion 49, 104019.Google Scholar
Martin, P., Baruzzo, M., Bialek, J., Bolzonella, T., Bonfiglio, D., Cavazzana, R., Chacon, L., Ferraro, N., Garofalo, A., Hanson, J. M. et al. 2015 Extreme low-edge safety factor tokamak scenarios via active control of three dimensional magnetic fields on RFX and DIII-D. In Proceedings of 25th International Fusion Energy Conference St Petersburg, Russian Federation 13–18 October 2014, EX/P2-41, IAEA.Google Scholar
Meade, D., Arunasalam, V., Barnes, C., Bell, M., Bitter, M., Budny, R., Cecchi, J., Cohen, S., Daughney, C., Davis, S. et al. 1980 PDX experimental results. In Plasma Physics and Controlled Nuclear Fusion Research 1980 (Proceedings of 8th International Conference Brussels, 1980), vol. 1, p. 665. IAEA.Google Scholar
Medvedev, S. Yu., Hender, T. C., Sauter, O. & Villard, L.2001 Theoretical MHD limits in tokamaks with a separatrix. In Proceedings of 28th EPS Conference on Contr. Fusion and Plasma Physics, Funchal 18–22 June 2001, ECA, (EPS, Petit Lancy, 2001), vol. 25A, pp. 21–24.Google Scholar
Medvedev, S. Yu., Martynov, A. A., Martin, Y. R., Sauter, O. & Villard, L. 2006 Edge kink/ballooning Mode Stability in Tokamaks with separatrix. Plasma Phys. Control. Fusion 48, 927–938.CrossRefGoogle Scholar
Okabayashi, M., Bol, K., Chance, M., Couture, P., Fishman, H., Fonck, R. J., Gammel, G., Heidbrink, W. W., Ida, K., Jaehning, K. P. et al. 1987 Stability and confinement studies in the princeton beta experiment (PBX). In Plasma Physics and Controlled Fusion Research Conference, Kyoto, Japan, 1986, vol. 1, pp. 275–290. IAEA.Google Scholar
Okabayashi, M., Bialek, J., Chance, M. S., Chu, M. S., Fredrickson, E. D., Garofalo, A. M., Hatcher, R., Jensen, T. H., Johnson, L. C., La Haye, R. J. et al. 2002 Stabilization of the resistive wall mode in DIII–D by plasma rotation and magnetic feedback. Plasma Phys. Control. Fusion 44, B339–B355.Google Scholar
Pfeiffer, W. W., Davidson, R. H., Miller, R. L. & Waltz, R. E.1980 ONETWO: a computer code for modeling plasma transport in tokamaks, General Atomics Report GA-A16178.Google Scholar
Piovesan, P., Hanson, J. M., Martin, P., Navratil, G. A., Turco, F., Bialek, J., La Haye, R. J., Lanctot, M. J., Okabayashi, M., Paz-Soldan, C. et al. 2014 Tokamak operation with safety factor $q95<2$ via control of MHD stability. Phys. Rev. Lett. 113, 045003.Google Scholar
Piron, C., Martin, P., Bonfiglio, D., Hanson, J., Logan, N., Paz-Soldan, C., Piovesan, P., Turco, F., Bialek, J., Franz, P. et al. 2016 Interaction of external $n=1$ magnetic fields with the sawtooth instability in low-q RFX-mod and DIII-D tokamaks. (in preparation).Google Scholar
Rice, B. W., Burrell, K. H., Lao, L. L. & Lin-Liu, Y. R. 1997 Direct measurement of the radial electric field in tokamak plasmas using the Stark effect. Phys. Rev. Lett. 79, 2694–2697.Google Scholar
Sabbagh, S. A., Sontag, A. C., Bialek, J. M., Gates, D. A., Glasser, A. H., Menard, J. E., Zhu, W., Bell, M. G., Bell, R. E., Bondeson, A. et al. 2006 Resistive wall stabilized operation in rotating high beta NSTX plasmas. Nucl. Fusion 46, 635–644.CrossRefGoogle Scholar
St. John, H., Taylor, T. S., Lin-Liu, Y. R. & Turnbull, A. D. 1994 Transport simulation of negative magnetic shear discharges. In Plasma Physics and Controlled Nuclear Fusion Research (Proceedings of 15th International Fusion Energy Conference Sevilla, Spain, October 1994), vol. 3, pp. 603–614. IAEA.Google Scholar
Sauter, O., Angioni, C. & Lin-Liu, Y. R. 1999 Neoclassical conductivity and bootstrap current formulas for general axisymmetric equilibria and arbitrary collision regime. Phys. Plasmas 6, 2834–2839.Google Scholar
Sauter, O., Westerhof, E., Mayoral, M. L., Alper, B., Belo, P. A., Buttery, R. J., Gondhalekar, A., Hellsten, T., Hender, T. C., Howell, D. F. et al. 2002 Control of neoclassical tearing modes by sawtooth control. Phys. Rev. Lett. 88, 105001.Google Scholar
Shafranov, V. D. 1970 Hydromagnetic stability of a current carrying pinch in a strong longitudinal magnetic field. Sov. Phys. Tech. Phys. 15, 175–183.Google Scholar
Spitzer, L. 1962 Physics of Fully Ionized Gases. Interscience.Google Scholar
Stambaugh, R., Allen, S., Bramson, G., Brooks, N., Burrell, K. H., Callis, R., Carlstrom, T., Chance, M., Chu, M., Colleraine, A. et al. 1988 High beta and ECRH studies in DIII-D. Plasma Phys. Control. Fusion 30, 1585–1596.CrossRefGoogle Scholar
Strait, E. J., Taylor, T. S., Turnbull, A. D., Ferron, J. R., Lao, L. L., Rice, B., Sauter, O., Thompson, S. J. & Wróblewski, D. 1995 Wall stabilization of high beta tokamak discharges in DIII-D. Phys. Rev. Lett. 74, 2483–2486.Google Scholar
Strait, E. J., Bialek, J., Bogatu, N., Chance, M. S. & Chu, M. S. 2003 Resistive wall stabilization of high-beta plasmas in DIII–D. Nucl. Fusion 43, 430–440.Google Scholar
Takeji, S., Tokuda, S., Fujita, T., Suzuki, T., Isayama, A., Ide, S., Ishii, Y., Kamada, Y., Koide, Y., Matsumoto, T. et al. 2002 Resistive instabilities in reversed shear discharges and wall stabilization on JT-60U. Nucl. Fusion 42, 634–636.Google Scholar
Troyon, F., Gruber, R., Saurenmann, H., Semenzato, S. & Succi, S. 1984 MHD limits to plasma confinement. Plasma Phys. Control. Fusion 26, 209–215.Google Scholar
Turnbull, A. D., Yasseen, F., Roy, A., Sauter, O., Cooper, W. A., Nicli, S. & Troyon, F. 1989 Low n ideal MHD stability of tokamaks: current and beta limits. Nucl. Fusion 29, 629–639.Google Scholar
Turnbull, A. D. & Troyon, F. 1989 Toroidal effects on current driven modes in tokamaks. Nucl. Fusion 29, 1887–1898.Google Scholar
Turnbull, A. D., Pearlstein, L. D., Bulmer, R. H., Lao, L. L. & La Haye, R. J. 1999 On the operational ideal MHD ${\it\beta}$ limit in sawtoothing discharges. Nucl. Fusion 39, 1557–1565.Google Scholar
Turnbull, A. D., Synder, P. B., Brennan, D. P., Chu, M. S. & Lao, L. L. 2005 Theory and simulation basis for magnetohydrodynamic stability in DIII-D. Fusion Sci. Technol. 48, 875–905.Google Scholar
Wesson, J. A. 1978 Hydromagnetic stability of tokamaks. Nucl. Fusion 18, 87–132.Google Scholar
Wesson, J. A. 1986 Sawtooth oscillations. Plasma Phys. Control. Fusion 28, 243–248.Google Scholar
Wesson, J. A. 1987 Tokamaks. Oxford University Press.Google Scholar
Zakharov, L. & Putvinskii, S. V. 1987 Effect of plasma rotation in a tokamak on the stabilizing effect of a conducting wall. Sov. J. Plasma Phys. 13, 68.Google Scholar