Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T10:16:15.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Electron phase-space hole transverse instability at high magnetic field

Published online by Cambridge University Press:  04 September 2019

I. H. Hutchinson Open the ORCID record for I. H. Hutchinson [Opens in a new window]
I. H. Hutchinson*
Affiliation:
Plasma Science and Fusion Center, MIT, Cambridge, MA, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Analytic treatment is presented of the electrostatic instability of an initially planar electron hole in a plasma of effectively infinite particle magnetization. It is shown that there is an unstable mode consisting of a rigid shift of the hole in the trapping direction. Its low frequency is determined by the real part of the force balance between the Maxwell stress arising from the transverse wavenumber 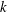$k$ and the kinematic jetting from the hole’s acceleration. The very low growth rate arises from a delicate balance in the imaginary part of the force between the passing-particle jetting, which is destabilizing, and the resonant response of the trapped particles, which is stabilizing. Nearly universal scalings of the complex frequency and 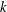$k$ with hole depth are derived. Particle in cell simulations show that the slow-growing instabilities previously investigated as coupled hole–wave phenomena occur at the predicted frequency, but with growth rates 2 to 4 times greater than the analytic prediction. This higher rate may be caused by a reduced resonant stabilization because of numerical phase-space diffusion in the simulations.

Keywords

plasma instabilitiesplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 5 , October 2019 , 905850501
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, L., Ergun, R. E., Tao, J., Roux, A., Lecontel, O., Angelopoulos, V., Bonnell, J., McFadden, J. P., Larson, D. E., Eriksson, S. et al. 2009 New features of electron phase space holes observed by the THEMIS mission. Phys. Rev. Lett. 102 (22), 225004.Google Scholar
Bale, S. D., Kellogg, P. J., Larsen, D. E., Lin, R. P., Goetz, K. & Lepping, R. P. 1998 Bipolar electrostatic structures in the shock transition region: Evidence of electron phase space holes. Geophys. Res. Lett. 25 (15), 2929–2932.Google Scholar
Berk, H. L., Nielsen, C. E. & Roberts, K. V. 1970 Phase Space Hydrodynamics of Equivalent Nonlinear Systems: Experimental and Computational Observations. Phys. Fluids 13 (4), 980.Google Scholar
Bernstein, I. B., Greene, J. M. & Kruskal, M. D. 1957 Exact nonlinear plasma oscillations. Phys. Rev. 108 (4), 546–550.Google Scholar
Berthomier, M., Muschietti, L., Bonnell, J. W., Roth, I. & Carlson, C. W. 2002 Interaction between electrostatic whistlers and electron holes in the auroral region. J. Geophys. Res. Space Phys. 107 (A12), 1–11.Google Scholar
Eliasson, B. & Shukla, P. K. 2006 Formation and dynamics of coherent structures involving phase-space vortices in plasmas. Phys. Rep. 422 (6), 225–290.Google Scholar
Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S., Muschietti, L., Roth, I. & Strangeway, R. J. 1998 Debye-Scale Plasma Structures Associated with Magnetic-Field-Aligned Electric Fields. Phys. Rev. Lett. 81 (4), 826–829.Google Scholar
Goldman, M. V., Oppenheim, M. M. & Newman, D. L. 1999 Nonlinear two-stream instabilities as an explanation for auroral bipolar wave structures. Geophys. Res. Lett. 26 (13), 1821–1824.Google Scholar
Hutchinson, I. H. 2011 Nonlinear collisionless plasma wakes of small particles. Phys. Plasmas 18, 032111.Google Scholar
Hutchinson, I. H. 2017 Electron holes in phase space: What they are and why they matter. Phys. Plasmas 24 (5), 055601.Google Scholar
Hutchinson, I. H. 2018a Kinematic mechanism of plasma electron hole transverse instability. Phys. Rev. Lett. 120 (20), 205101.Google Scholar
Hutchinson, I. H. 2018b Transverse instability of electron phase-space holes in multi-dimensional Maxwellian plasmas. J. Plasma Phys. 84, 905840411.Google Scholar
Hutchinson, I. H. 2019 Transverse instability magnetic field thresholds of electron phase-space holes. Phys. Rev. E 99, 053209.Google Scholar
Hutchinson, I. H., Haakonsen, C. B. & Zhou, C. 2015 Non-linear plasma wake growth of electron holes. Phys. Plasmas 22 (3), 32312.Google Scholar
Hutchinson, I. H. & Malaspina, D. M. 2018 Prediction and Observation of Electron Instabilities and Phase Space Holes Concentrated in the Lunar Plasma Wake. Geophys. Res. Lett. 45, 3838–3845.Google Scholar
Hutchinson, I. H. & Zhou, C. 2016 Plasma electron hole kinematics. I. Momentum conservation. Phys. Plasmas 23 (8), 82101.Google Scholar
Jovanović, D. & Schamel, H. 2002 The stability of propagating slab electron holes in a magnetized plasma. Phys. Plasmas 9 (12), 5079–5087.Google Scholar
Lashmore-Davies, C. N. 2005 Negative energy waves. J. Plasma Phys. 71, 101–109.Google Scholar
Lu, Q. M., Lembege, B., Tao, J. B. & Wang, S. 2008 Perpendicular electric field in two-dimensional electron phase-holes: a parameter study. J. Geophys. Res. 113 (A11), A11219.Google Scholar
Malaspina, D. M., Andersson, L., Ergun, R. E., Wygant, J. R., Bonnell, J. W., Kletzing, C., Reeves, G. D., Skoug, R. M. & Larsen, B. A. 2014 Nonlinear electric field structures in the inner magnetosphere. Geophys. Res. Lett. 41, 5693–5701.Google Scholar
Malaspina, D. M., Newman, D. L., Willson, L. B., Goetz, K., Kellogg, P. J. & Kerstin, K. 2013 Electrostatic solitary waves in the solar wind: evidence for instability at solar wind current sheets. J. Geophys. Res.: Space Phys. 118 (2), 591–599.Google Scholar
Mangeney, A., Salem, C., Lacombe, C., Bougeret, J.-L., Perche, C., Manning, R., Kellogg, P. J., Goetz, K., Monson, S. J. & Bosqued, J.-M. 1999 WIND observations of coherent electrostatic waves in the solar wind. Ann. Geophys. 17 (3), 307–320.Google Scholar
Matsumoto, H., Kojima, H., Miyatake, T., Omura, Y., Okada, M., Nagano, I. & Tsutsui, M. 1994 Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys. Res. Lett. 21 (25), 2915–2918.Google Scholar
Miyake, T., Omura, Y., Matsumoto, H. & Kojima, H. 1998 Two-dimensional computer simulations of electrostatic solitary waves observed by Geotail spacecraft. J. Geophys. Res. 103 (A6), 11841.Google Scholar
Morse, R. L. & Nielson, C. W. 1969 One-, two-, and three-dimensional numerical simulation of two-Beam plasmas. Phys. Rev. Lett. 23 (19), 1087–1090.Google Scholar
Mottez, F., Perraut, S., Roux, A. & Louarn, P. 1997 Coherent structures in the magnetotail triggered by counterstreaming electron beams. J. Geophys. Res. 102 (A6), 11399.Google Scholar
Mozer, F. S., Agapitov, O. A., Artemyev, A., Burch, J. L., Ergun, R. E., Giles, B. L., Mourenas, D., Torbert, R. B., Phan, T. D. & Vasko, I. 2016 Magnetospheric multiscale satellite observations of parallel electron acceleration in magnetic field reconnection by fermi reflection from time domain structures. Phys. Rev. Lett. 116 (14), 4–8.Google Scholar
Mozer, F. S., Agapitov, O. V., Giles, B. & Vasko, I. 2018 Direct observation of electron distributions inside millisecond duration electron holes. Phys. Rev. Lett. 121 (13), 135102.Google Scholar
Muschietti, L., Roth, I., Carlson, C. W. & Ergun, R. E. 2000 Transverse instability of magnetized electron holes. Phys. Rev. Lett. 85 (1), 94–97.Google Scholar
Newman, D. L., Goldman, M. V., Spector, M. & Perez, F. 2001 Dynamics and instability of electron phase-space tubes. Phys. Rev. Lett. 86 (7), 1239–1242.Google Scholar
Oppenheim, M., Newman, D. L. & Goldman, M. V. 1999 Evolution of electron phase-space holes in a 2D magnetized plasma. Phys. Rev. Lett. 83 (12), 2344–2347.Google Scholar
Oppenheim, M. M., Vetoulis, G., Newman, D. L. & Goldman, M. V. 2001 Evolution of electron phase-space holes in 3D. Geophys. Res. Lett. 28 (9), 1891–1894.Google Scholar
Pickett, J. S., Chen, L.-J., Mutel, R. L., Christopher, I. W., Santol’k, O., Lakhina, G. S., Singh, S. V., Reddy, R. V., Gurnett, D. A., Tsurutani, B. T. et al. 2008 Furthering our understanding of electrostatic solitary waves through Cluster multispacecraft observations and theory. Adv. Space Res. 41 (10), 1666–1676.Google Scholar
Schamel, H. 1986 Electrostatic phase space structures in theory and experiment. Phys. Rep. 140 (3), 161–191.Google Scholar
Singh, N., Loo, S. M. & Wells, B. E. 2001a Electron hole as an antenna radiating plasmawaves. Geophys. Res. Lett. 28 (7), 1371–1374.Google Scholar
Singh, N., Loo, S. M. & Wells, B. E. 2001b Electron hole structure and its stability depending on plasma magnetization. J. Geophys. Res. 106 (A10), 21183–21198.Google Scholar
Turikov, V. A. 1984 Electron phase space holes as localized BGK solutions. Phys. Scr. 30 (1), 73–77.Google Scholar
Umeda, T. 2008 Generation of low-frequency electrostatic and electromagnetic waves as nonlinear consequences of beam plasma interactions. Phys. Plasmas 15, 064502.Google Scholar
Umeda, T., Omura, Y., Miyake, T., Matsumoto, H. & Ashour-Abdalla, M. 2006 Nonlinear evolution of the electron two-stream instability: two-dimensional particle simulations. J. Geophys. Res.: Space Phys. 111 (10), 1–9.Google Scholar
Vasko, I. Y., Agapitov, O. V., Mozer, F., Artemyev, A. V. & Jovanovic, D. 2015 Magnetic field depression within electron holes. Geophys. Res. Lett. 42 (7), 2123–2129.Google Scholar
Vetoulis, G. & Oppenheim, M. 2001 Electrostatic mode excitation in electron holes due to wave bounce resonances. Phys. Rev. Lett. 86 (7), 1235–1238.Google Scholar
Wilson, L. B., Cattell, C. A., Kellogg, P. J., Goetz, K., Kersten, K., Kasper, J. C., Szabo, A. & Wilber, M. 2010 Large-amplitude electrostatic waves observed at a supercritical interplanetary shock. J. Geophys. Res.: Space Phys. 115 (12), A12104.Google Scholar
Wu, M., Lu, Q., Huang, C. & Wang, S. 2010 Transverse instability and perpendicular electric field in two-dimensional electron phase-space holes. J. Geophys. Res.: Space Phys. 115 (10), A10245.Google Scholar
Zhou, C. & Hutchinson, I. H. 2017 Plasma electron hole ion-acoustic instability. J. Plasma Phys. 83, 90580501.Google Scholar