Article contents
Efficient kinetic Lattice Boltzmann simulation of three-dimensional Hall-MHD turbulence
Published online by Cambridge University Press: 08 August 2023
Abstract
Simulating plasmas in the Hall-magnetohydrodynamics (Hall-MHD) regime represents a valuable approach for the investigation of complex nonlinear dynamics developing in astrophysical frameworks and fusion machines. The Hall electric field is computationally very challenging as it involves the integration of an additional term, proportional to $\boldsymbol {\nabla } \times ((\boldsymbol {\nabla }\times \boldsymbol {B})\times \boldsymbol {B})$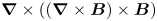 , in Faraday's induction law. The latter feeds back on the magnetic field $B$
, in Faraday's induction law. The latter feeds back on the magnetic field $B$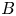 at small scales (between the ion and electron inertial scales), requiring very high resolutions in both space and time to properly describe its dynamics. The computational advantage provided by the kinetic lattice Boltzmann (LB) approach is exploited here to develop a new code, the fast lattice-Boltzmann algorithm for MHD experiments (flame). The flame code integrates the plasma dynamics in lattice units coupling two kinetic schemes, one for the fluid protons (including the Lorentz force), the other to solve the induction equation describing the evolution of the magnetic field. Here, the newly developed algorithm is tested against an analytical wave-solution of the dissipative Hall-MHD equations, pointing out its stability and second-order convergence, over a wide range of the control parameters. Spectral properties of the simulated plasma are finally compared with those obtained from numerical solutions from the well-established pseudo-spectral code ghost. Furthermore, the LB simulations we present, varying the Hall parameter, highlight the transition from the MHD to the Hall-MHD regime, in excellent agreement with the magnetic field spectra measured in the solar wind.
at small scales (between the ion and electron inertial scales), requiring very high resolutions in both space and time to properly describe its dynamics. The computational advantage provided by the kinetic lattice Boltzmann (LB) approach is exploited here to develop a new code, the fast lattice-Boltzmann algorithm for MHD experiments (flame). The flame code integrates the plasma dynamics in lattice units coupling two kinetic schemes, one for the fluid protons (including the Lorentz force), the other to solve the induction equation describing the evolution of the magnetic field. Here, the newly developed algorithm is tested against an analytical wave-solution of the dissipative Hall-MHD equations, pointing out its stability and second-order convergence, over a wide range of the control parameters. Spectral properties of the simulated plasma are finally compared with those obtained from numerical solutions from the well-established pseudo-spectral code ghost. Furthermore, the LB simulations we present, varying the Hall parameter, highlight the transition from the MHD to the Hall-MHD regime, in excellent agreement with the magnetic field spectra measured in the solar wind.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by



