Published online by Cambridge University Press: 21 September 2015
The properties of dust acoustic and drift waves are investigated in a charge varying magnetized dusty plasma. The plasma is composed of non-thermal electrons and ions with dynamic dust particles. The mathematical expression which describes the dust charge fluctuation is obtained using  ${\it\kappa}$-distribution for both the electrons and ions. A dispersion relation is derived and analysed numerically by choosing space plasma parameters. It is found that the inclusion of variable dust charge along with the non-thermal effects of electrons and ions significantly affect linear/nonlinear properties of the dust acoustic and dust drift waves. The effects of different physical parameters including spectral index (
${\it\kappa}$-distribution for both the electrons and ions. A dispersion relation is derived and analysed numerically by choosing space plasma parameters. It is found that the inclusion of variable dust charge along with the non-thermal effects of electrons and ions significantly affect linear/nonlinear properties of the dust acoustic and dust drift waves. The effects of different physical parameters including spectral index ( ${\it\kappa}$), dust charge number (
${\it\kappa}$), dust charge number (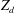 $Z_{d}$), electron density (
$Z_{d}$), electron density (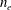 $n_{e}$) and ion temperature (
$n_{e}$) and ion temperature (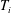 $T_{i}$) on the wave dispersion and instability are presented. It is found that the presence of the non-thermal electron and ion populations reduce the growth rate of the instability which arises due to the dust charging effect. In addition, the nonlinear vortex solutions are also obtained. For illustration, the results are analysed by using the dusty plasma parameters of Saturn’s magnetosphere.
$T_{i}$) on the wave dispersion and instability are presented. It is found that the presence of the non-thermal electron and ion populations reduce the growth rate of the instability which arises due to the dust charging effect. In addition, the nonlinear vortex solutions are also obtained. For illustration, the results are analysed by using the dusty plasma parameters of Saturn’s magnetosphere.