Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T04:17:42.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusive time evolution of the Grad–Shafranov equation for a toroidal plasma

Part of: Focus on Fusion Laboratory and Astrophysical Plasmas: New Perspectives

Published online by Cambridge University Press:  11 June 2021

Giovanni Montani Open the ORCID record for Giovanni Montani [Opens in a new window] ,
Matteo Del Prete Open the ORCID record for Matteo Del Prete [Opens in a new window] ,
Nakia Carlevaro Open the ORCID record for Nakia Carlevaro [Opens in a new window]  and
Francesco Cianfrani
Giovanni Montani
Affiliation:
ENEA, Fusion and Nuclear Safety Department, C.R. Frascati, Via E. Fermi 45, 00044Frascati (Roma), Italy Physics Department, “Sapienza” University of Rome, P.le Aldo Moro 5, 00185Roma, Italy
Matteo Del Prete*
Affiliation:
Physics Department, “Sapienza” University of Rome, P.le Aldo Moro 5, 00185Roma, Italy
Nakia Carlevaro
Affiliation:
ENEA, Fusion and Nuclear Safety Department, C.R. Frascati, Via E. Fermi 45, 00044Frascati (Roma), Italy CREATE Consortium, Via Claudio 21, 80125Napoli, Italy
Francesco Cianfrani
Affiliation:
PIIM UMR7345, CNRS, Aix-Marseille University, Jardin du Pharo, 58 Boulevard Charles Livon, 13007Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the evolution of a plasma equilibrium having a toroidal topology in the presence of constant electric resistivity. After outlining the main analytical properties of the solution, we illustrate its physical implications by reproducing the essential features of a scenario for the upcoming Italian experiment Divertor Tokamak Test Facility, with a good degree of accuracy. Although we find the resistive diffusion time scale to be of the order of $10^4$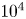 s, we observe a macroscopic change in the plasma volume on a time scale of $10^2$ 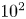s, comparable to the foreseen duration of the plasma discharge by design. In the final part of the work, we compare our self-consistent solution to the more common Solov'ev one, and to a family of nonlinear configurations.

Keywords

plasma confinementplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 3 , June 2021 , 845870301
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Albanese, R., Crisanti, F., Martin, P., Martone, R., Pizzuto, A. & Project Proposal Contributors, DTT 2019 Divertor tokamak test facility, interim design report. Tech. Rep. ENEA.Google Scholar
Albanese, R. & Pizzuto, A. 2017 The DTT proposal, a tokamak facility to address exhaust challenges for demo: introduction and executive summary. Fusion Engng Des. 122, 274–284.CrossRefGoogle Scholar
Alladio, F. & Crisanti, F. 1986 Analysis of MHD equilibria by toroidal multipolar expansions. Nucl. Fusion 26 (9), 1143–1164.CrossRefGoogle Scholar
Alladio, F., Micozzi, P., Apruzzese, G. M., Boncagni, L., D'Arcangelo, O., Giovannozzi, E., Grosso, L. A., Iafrati, M., Lampasi, A., Maffia, G., Mancuso, A., Piergotti, V., Rocchi, G., Sibio, A., Tilia, B., Tudisco, O. & Zanza, V. 2017 The PROTO-SPHERA experiment, an innovative confinement scheme for fusion. In 19th International Spherical Torus Workshop (ISTW 2017), Seoul National University, 18-22 September 2017.Google Scholar
Biskamp, D. 1993 Nonlinear Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Dini, F., Baghdadi, R., Amrollahi, R. & Khorasani, S. 2011 An overview of plasma confinement in toroidal systems. Horizons World Phys. 271, 71.Google Scholar
Grad, H. 1974 Classical Plasma Diffusion. Adv. Plasma Phys. 5, 103.Google Scholar
Grad, H. & Hogan, J. 1970 Classical diffusion in a tokomak. Phys. Rev. Lett. 24 (24), 1337–1340.CrossRefGoogle Scholar
Grad, H. & Hu, P. N. 1977 Classical diffusion: theory and simulation codes. Tech. Rep. United States, CONF-7709167.Google Scholar
Grad, H., Hu, P. N. & Stevens, D. C. 1975 Adiabatic evolution of plasma equilibrium. Proc. Natl Acad. Sci. 72 (10), 3789–3793.CrossRefGoogle ScholarPubMed
Grad, H., Hu, P. N., Stevens, D. C. & Turkel, E. 1977 Classical plasma diffusion. In Plasma Physics and Controlled Nuclear Fusion Research 1976, vol. 2, pp. 355–365. International Atomic Energy Agency.Google Scholar
Grad, H. & Rubin, H. 1958 Hydromagnetic equilibria and force-free fields. In Proceedings of the 2nd United Nations Conference Peaceful Uses of Atomic Energy, vol. 31, p. 190. United Nations Publications.Google Scholar
Keilhacker, M. 1987 H-mode confinement in tokamaks. Plasma Phys. Control. Fusion 29 (10A), 1401–1413.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1984 Chapter VIII - magnetohydrodynamics. In Electrodynamics of Continuous Media, 2nd edn (ed. L. D. Landau & E. M. Lifshitz), Course of Theoretical Physics, vol. 8, pp. 225–256. Pergamon.CrossRefGoogle Scholar
Lao, L. L., St. John, H., Stambaugh, R. D., Kellman, A. G. & Pfeiffer, W. 1985 Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 25 (11), 1611–1622.CrossRefGoogle Scholar
Mc Carthy, P. J. 1999 Analytical solutions to the Grad-Shafranov equation for tokamak equilibrium with dissimilar source functions. Phys. Plasmas 6 (9), 3554–3560.CrossRefGoogle Scholar
Miller, G. 1985 Resistive evolution of general plasma configurations. Phys. Fluids 28 (5), 1354–1358.CrossRefGoogle Scholar
Montani, G., Rizzo, M. & Carlevaro, N. 2018 Behavior of thin disk crystalline morphology in the presence of corrections to ideal magnetohydrodynamics. Phys. Rev. E 97 (2), 023205. arXiv:1802.10506.CrossRefGoogle ScholarPubMed
Nedospasov, A. V. 2008 Thermal quench in tokamaks. Nucl. Fusion 48 (3), 032002.CrossRefGoogle Scholar
Nührenberg, J. 1972 Special time-dependent solutions of diffuse tokamak equilibrium. Nucl. Fusion 12 (2), 157–163.CrossRefGoogle Scholar
Pao, Y. P. 1976 Classical diffusion in toroidal plasmas. Phys. Fluids 19 (8), 1177–1182.CrossRefGoogle Scholar
Reid, J. & Laing, E. W. 1979 The resistive evolution of force-free magnetic fields. Part 1. Slab geometry. J. Plasma Phys. 21 (3), 501–510.CrossRefGoogle Scholar
Rice, J. E. 2016 Experimental observations of driven and intrinsic rotation in tokamak plasmas. Plasma Phys. Control. Fusion 58 (8), 083001.CrossRefGoogle Scholar
Shafranov, V. D. 1966 Plasma equilibrium in a magnetic field. Rev. Plasma Phys. 2, 103.Google Scholar
Solov'ev, L. S. 1968 The theory of hydromagnetic stability of toroidal plasma configurations. Sov. J. Exp. Theor. Phys. 26, 400.Google Scholar
Spitzer, L. & Härm, R. 1953 Transport phenomena in a completely ionized gas. Phys. Rev. 89 (5), 977–981.CrossRefGoogle Scholar
Strand, P. I. & Houlberg, W. A. 2001 Magnetic flux evolution in highly shaped plasmas. Phys. Plasmas 8 (6), 2782–2792.CrossRefGoogle Scholar
Tamain, P., Bufferand, H., Ciraolo, G., Colin, C., Galassi, D., Ghendrih, P., Schwander, F. & Serre, E. 2016 The tokam3x code for edge turbulence fluid simulations of tokamak plasmas in versatile magnetic geometries. J. Comput. Phys. 321, 606–623.CrossRefGoogle Scholar
Wagner, F., et al. 1984 Development of an edge transport barrier at the H-mode transition of ASDEX. Phys. Rev. Lett. 53 (15), 1453–1456.CrossRefGoogle Scholar
Wagner, F. 2007 A quarter-century of H-mode studies. Plasma Phys. Control. Fusion 49 (12B), B1–B33.CrossRefGoogle Scholar
Wesson, J. 2011 Tokamaks, 4th edn. International Series of Monographs in Physics. Oxford Science Publications.Google Scholar