Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T14:37:19.703Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of the growth rate for the linearized Zakharov—Kuznetsov equation

Published online by Cambridge University Press:  13 March 2009

M. A. Allen  and
G. Rowlands
M. A. Allen
Affiliation:
Department of Physics, University of Warwick, Coventry CV4 7AL, U.K.
G. Rowlands
Affiliation:
Department of Physics, University of Warwick, Coventry CV4 7AL, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

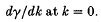Studies of the Zakharov—Kuznetsov equation governing solitons in a strongly magnetized ion-acoustic plasma indicate that a perturbed flat soliton is unstable and evolves into higher-dimensional solitons. The growth rate γ = γ(k) of a small sinusoidal perturbation of wavenumber k to a flat soliton has already been found numerically, and lengthy analytical work has given the value of We introduce a more direct analytical method in the form of an extension to the usual multiple-scale perturbation approach and use it to determine a consistent expansion of γ about k = 0 and the other zero at k2 = 5.By combining these results in the form of a two-point Padé approximant, we obtain an analytical expression for γ valid over the entire range of k for which the solution is unstable. We also present a very efficient numerical method for determining the growth rate curve to great accuracy. The Padé approximant gives excellent agreement with the numerical results.

Type
Research Article
Information
Journal of Plasma Physics , Volume 50 , Issue 3 , December 1993 , pp. 413 - 424
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, G. A. & Graves-Morris, P. 1984 Padé Approximants. Cambridge University Press.Google Scholar
Frycz, P. & Infeld, E. 1989a J. Plasma Phys. 41, 441.Google Scholar
Frucz, P. & Infeld, E. 1989b Phys. Rev. Lett. 63, 384.CrossRefGoogle Scholar
Frycz, P., Infeld, E. & Samson, J. C. 1992 Phys. Rev. Lett. 69, 1057.CrossRefGoogle Scholar
Infeld, E. 1985 J. Plasma Phys. 33, 171.CrossRefGoogle Scholar
Infeld, E. & Frycz, P. 1987 J. Plasma Phys. 37, 97.Google Scholar
Infeld, E. & Rowlands, G. 1977 Plasma Phys. 19, 343.Google Scholar
Infeld, E. & Rowlands, G. 1990 Nonlinear Waves, Solitons and Chaos. Cambridge University Press.Google Scholar
Laedke, E. W. & Spatschek, K. H. 1982 J. Plasma Phys. 28, 469.Google Scholar
Makhankov, V. G. 1978 Phys. Rep. 35, 1.CrossRefGoogle Scholar
Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. 1988 Numerical Recipes in C. Cambridge University Press.Google Scholar
Rowlands, G. 1990 Non-Linear Phenomena in Science and Engineering. Ellis Horwood.Google Scholar
Wolfram, S. 1991 Mathematica. Addison-Wesley.Google Scholar
Zakharov, V. B. & Kuznetsov, E. A. 1974 Soviet Phys. JETP 39, 285.Google Scholar