Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jorge, R.
Frei, B. J.
and
Ricci, P.
2019.
Nonlinear gyrokinetic Coulomb collision operator.
Journal of Plasma Physics,
Vol. 85,
Issue. 6,
Francisquez, M.
Bernard, T.N.
Mandell, N.R.
Hammett, G.W.
and
Hakim, A.
2020.
Conservative discontinuous Galerkin scheme of a gyro-averaged Dougherty collision operator.
Nuclear Fusion,
Vol. 60,
Issue. 9,
p.
096021.
Juno, J.
Swisdak, M. M.
Tenbarge, J. M.
Skoutnev, V.
and
Hakim, A.
2020.
Noise-induced magnetic field saturation in kinetic simulations.
Journal of Plasma Physics,
Vol. 86,
Issue. 4,
Perrone, L. M.
Jorge, R.
and
Ricci, P.
2020.
Four-dimensional drift-kinetic model for scrape-off layer plasmas.
Physics of Plasmas,
Vol. 27,
Issue. 11,
Hakim, Ammar H.
Mandell, Noah R.
Bernard, T. N.
Francisquez, M.
Hammett, G. W.
and
Shi, E. L.
2020.
Continuum electromagnetic gyrokinetic simulations of turbulence in the tokamak scrape-off layer and laboratory devices.
Physics of Plasmas,
Vol. 27,
Issue. 4,
Hakim, Ammar
and
Juno, James
2020.
Alias-Free, Matrix-Free, and Quadrature-Free Discontinuous Galerkin Algorithms for (Plasma) Kinetic Equations.
p.
1.
Tyranowski, Tomasz M.
2021.
Stochastic variational principles for the collisional Vlasov–Maxwell and Vlasov–Poisson equations.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 477,
Issue. 2252,
Taitano, W.T.
Chacón, L.
Simakov, A.N.
and
Anderson, S.E.
2021.
A conservative phase-space moving-grid strategy for a 1D-2V Vlasov–Fokker–Planck Solver.
Computer Physics Communications,
Vol. 258,
Issue. ,
p.
107547.
Jenab, Seyyed Mehdi Hosseini
Brodin, Gert
Juno, James
and
Kourakis, Ioannis
2021.
Ultrafast electron holes in plasma phase space dynamics.
Scientific Reports,
Vol. 11,
Issue. 1,
Pezzi, O
Liang, H
Juno, J L
Cassak, P A
Vásconez, C L
Sorriso-Valvo, L
Perrone, D
Servidio, S
Roytershteyn, V
TenBarge, J M
and
Matthaeus, W H
2021.
Dissipation measures in weakly collisional plasmas.
Monthly Notices of the Royal Astronomical Society,
Vol. 505,
Issue. 4,
p.
4857.
Endeve, Eirik
and
Hauck, Cory D.
2022.
Conservative DG method for the micro-macro decomposition of the Vlasov–Poisson–Lenard–Bernstein model.
Journal of Computational Physics,
Vol. 462,
Issue. ,
p.
111227.
Ulbl, Philipp
Michels, Dominik
and
Jenko, Frank
2022.
Implementation and verification of a conservative,multi‐species,gyro‐averaged, full‐f,Lenard‐Bernstein/Dougherty collision operator in the gyrokinetic codeGENE‐X.
Contributions to Plasma Physics,
Vol. 62,
Issue. 5-6,
Francisquez, Manaure
Juno, James
Hakim, Ammar
Hammett, Gregory W.
and
Ernst, Darin R.
2022.
Improved multispecies Dougherty collisions.
Journal of Plasma Physics,
Vol. 88,
Issue. 3,
Kim, Dongkyu
Seo, Janghoon
Jo, Gahyung
Kwon, Jae-Min
and
Yoon, Eisung
2022.
Nonlinear Fokker-Planck collision operator in Rosenbluth form for gyrokinetic simulations using discontinuous Galerkin method.
Computer Physics Communications,
Vol. 279,
Issue. ,
p.
108459.
Bernard, T. N.
Halpern, F. D.
Francisquez, M.
Mandell, N. R.
Juno, J.
Hammett, G. W.
Hakim, A.
Wilkie, G. J.
and
Guterl, J.
2022.
Kinetic modeling of neutral transport for a continuum gyrokinetic code.
Physics of Plasmas,
Vol. 29,
Issue. 5,
Almuslimani, Ibrahim
and
Crouseilles, Nicolas
2023.
Conservative stabilized Runge-Kutta methods for the Vlasov-Fokker-Planck equation.
Journal of Computational Physics,
Vol. 488,
Issue. ,
p.
112241.
Skolar, C. R.
Bradshaw, K.
Juno, J.
and
Srinivasan, B.
2023.
Continuum kinetic investigation of the impact of bias potentials in the current saturation regime on sheath formation.
Physics of Plasmas,
Vol. 30,
Issue. 1,
Ulbl, Philipp
Body, Thomas
Zholobenko, Wladimir
Stegmeir, Andreas
Pfennig, Jan
and
Jenko, Frank
2023.
Influence of collisions on the validation of global gyrokinetic simulations in the edge and scrape-off layer of TCV.
Physics of Plasmas,
Vol. 30,
Issue. 5,
Juno, James
Brown, Collin R.
Howes, Gregory G.
Haggerty, Colby C.
TenBarge, Jason M.
Wilson III, Lynn B.
Caprioli, Damiano
and
Klein, Kristopher G.
2023.
Phase-space Energization of Ions in Oblique Shocks.
The Astrophysical Journal,
Vol. 944,
Issue. 1,
p.
15.
Cagas, Petr
Juno, James
Hakim, Ammar
LaJoie, Andrew
Chu, Feng
Langendorf, Samuel
and
Srinivasan, Bhuvana
2023.
An investigation of shock formation vs shock mitigation of colliding plasma jets.
Physics of Plasmas,
Vol. 30,
Issue. 5,
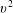 $v^{2}$ is not included in the basis set used in the discretization. A series of benchmark problems is presented and shows that the scheme conserves momentum and energy to machine precision. Empirical evidence also indicates that entropy is a non-decreasing function. The collision terms are combined with the Vlasov equation to study collisional Landau damping and plasma heating via magnetic pumping.
$v^{2}$ is not included in the basis set used in the discretization. A series of benchmark problems is presented and shows that the scheme conserves momentum and energy to machine precision. Empirical evidence also indicates that entropy is a non-decreasing function. The collision terms are combined with the Vlasov equation to study collisional Landau damping and plasma heating via magnetic pumping.