Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T21:07:09.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparative study of dust ion acoustic Korteweg–de Vries and modified Korteweg–de Vries solitons in dusty plasmas with variable temperatures

Published online by Cambridge University Press:  05 October 2017

B. C. Kalita  and
S. Das Open the ORCID record for S. Das [Opens in a new window]
B. C. Kalita
Affiliation:
Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India
S. Das*
Affiliation:
Department of Mathematics, Gauhati University, Guwahati-781014, Assam, India Department of Basic Sciences (Mathematics), Central Institute of Technology Kokrajhar, BTAD, Pin-783370, Assam, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this plasma model, consisting of ions and electrons with pressure variations in both the components in the presence of stationary dust, both compressive and rarefactive Korteweg–de Vries (KdV) solitons of interesting character are established. Based on high dust charge, characteristics of soliton growth are found to be amplified for various pairs of ion and electron streaming speeds. It is noteworthy to mention that for some pairs of ion and electron initial streaming speeds, only compressive KdV solitons with either decreasing or increasing growth are shown to reflect. Contrary to this, for some other pairs of ion and electron streaming speeds, the amplitudes of both rarefactive and compressive solitons are seen to be produced, changing from rarefactive to compressive growth. At the stationary background of the massive dust particles, the lighter particles suffer appreciable initial drifts (backwards streaming) which characteristically change the growth of solitons. For inclusion of higher-order nonlinearity, only compressive modified Korteweg–de Vries (MKdV) solitons of much higher amplitude are found to exist whereas for the same set of parameter values both compressive and rarefactive KdV solitons are found to exist. Smaller values of electron streaming speed are seen to produce high amplitude MKdV solitons. We also observe that due to higher-order nonlinearity, the nonlinear monotonic growth of amplitudes of MKdV solitons is supported by the almost equal streaming speed pairs of ions and electrons for relatively small values of 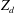$Z_{d}$, where 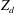$Z_{d}$ is the number of charges in a dust particle

Keywords

dusty plasmasplasma nonlinear phenomenaplasma waves
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 5 , October 2017 , 905830502
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asgari, H., Muniandy, S. V. & Wong, C. S. 2013 Dust-acoustic solitary waves in dusty plasmas with non-thermal ions. Phys. Plasmas 20, 023705.Google Scholar
Baluku, T. K. & Helberg, M. A. 2008 Dust acoustic solitons in plasmas with kappa-distributed electrons and/or ions. Phys. Plasmas 15, 123705.CrossRefGoogle Scholar
Barkan, A., Marlino, R. L. & D’Angelo, N. 1995 Laboratory observation of the dust-acoustic wave mode. Phys. Plasmas 2, 3563.Google Scholar
Barnes, M. S., Keller, J. H., Forster, J. C., O’Neill, J. A. & Coultas, D. K. 1992 Transport of dust particles in glow-discharge plasmas. Phys. Rev. Lett. 68, 313.Google Scholar
Cairns, R. A., Mamun, A. A., Bingham, R., Dendy, R., Boström, R., Nairn, C. M. C. & Shukla, P. K. 1995 Electrostatic solitary structures in non-thermal plasmas. Geophys. Res. Lett. 22, 2709.CrossRefGoogle Scholar
Chatterjee, P. & Roychoudhury, R. 1994 Effect of ion temperature on large amplitude ion-acoustic solitary waves in relativistic plasma. Phys. Plasmas 1, 2148.Google Scholar
Chow, V. W., Mendis, D. A. & Rosenberg, M. J. 1993 Role of grain size and particle velocity distribution in secondary electron emission in space plasmas. Geophys. Res. (Space Science) 98, 19065.CrossRefGoogle Scholar
EL-Labony, S. K. & EL-Taibany, W. F. 2003 Dust acoustic solitary waves and double layers in a dusty plasma with an arbitrary streaming ion beam. Phys. Plasmas 10, 989.Google Scholar
Das, G. C., Singh, S. S. & Singh, R. I. 1996 Propagation of various K-dV solitary waves in an inhomogeneous two temperature electron plasma. Chaos, Solitons Fractals 7, 309.Google Scholar
Ghosh, S., Choudhury, T. K., Sarkar, S., Khan, M. & Gupta, M. R. 2001 Small amplitude nonlinear dust acoustic wave propagation in Saturn’s f, g and e rings. Astrophys. Space Sci. 278, 465.Google Scholar
Ghosh, S., Sarkar, S., Khan, H. & Gupta, M. R. 2000 Dust ion acoustic shock waves in a collisionless dusty plasma. Phys. Lett. A 274, 162.Google Scholar
Kalita, B. C. & Barman, S. N. 1995 Solitons in a warm unmagnetized plasma with electron inertia and negative ions. J. Phys. Soc. Japan 64, 784.Google Scholar
Kalita, B. C. & Kalita, R. 2016 Implicit role of Cairns distributed ions and weak relativistic effects of electrons in the formation of dust acoustic waves in plasma. J. Plasma Phys. 82, 905820201.Google Scholar
Kopnin, S. I., Kosarev, I. N., Popel, S. I. & Yu, M. Y. 2005 Dust acoustic solitons in the dusty plasma of the Earth’s ionosphere. Plasma Phys. Rep. 31 (3), 198.Google Scholar
Kundu, N. R. & Mamun, A. A. 2012 Dust-ion-acoustic solitary waves in a dusty plasma with arbitrarily charged dust and non-thermal electrons. J. Plasma Phys. 78, 677.Google Scholar
Mamun, A. A. 1998 Nonlinear propagation of dust-acoustic waves in magnetized dusty plasma with vortex-like ion distribution. J. Plasma Phys. 59, 575.CrossRefGoogle Scholar
Mamun, A. A. 1999 Arbitrary amplitude dust-acoustic solitary structures in athree-component dusty plasma. Astrophys. Space Sci. 268, 443.Google Scholar
Mamun, A. A., Cairns, R. A. & D’Angelo, N. 1996 Effects of vortex-like and non-thermal ion distributions on non-linear dust-acoustic waves. Phys. Plasmas 3, 2610.Google Scholar
Masud, M. M., Asaduzzaman, M. & Mamun, A. A. 2012 Dust-ion-acoustic Gardner solitons in a dusty plasma with bi-Maxwellian electrons. Phys. Plasmas 19, 103706.Google Scholar
Mendis, D. A. & Rosenberg, M. 1994 Cosmic dusty plasma. Annu. Rev. Astron. Astrophys. 32, 419.Google Scholar
Nakamura, Y., Bailung, H. & Shukla, P. K. 1999 Observation of ion-acoustic shocks in a dusty plasma. Phys. Rev. Lett. 83, 1602.CrossRefGoogle Scholar
Nakamura, Y. & Sarma, A. 2001 Observation of ion-acoustic solitary waves in a dusty plasma. Phys. Plasmas 8, 3921.Google Scholar
Pakzad, H. R. 2009 Dust acoustic solitary waves in dusty plasma with non-thermal ions. Astrophys. Space Sci. 41, 324.Google Scholar
Popel, S. I., Andreev, S. N., Gisko, A. A., Golubo’, A. P. & Losseva, T. V. T. V. 2004 Dissipative processes during the propagation of nonlinear dust ion-acoustic perturbations. Plasma Phys. Rep. 30, 284.Google Scholar
Popel, S. I., Golubo’, A. P. & Losseva, T. V. 2001 Dust ion-acoustic shock-wave structures: theory and laboratory experiments. JETP Lett. 74, 362.Google Scholar
Rao, N. N., Shukla, P. K. & Yu, M. Y. 1990 Dust-Acoustic waves in dusty plasmas. Planet. Space Sci. 38, 543.Google Scholar
Rosengberg, M. 1993 Ion- and dust-acoustic instabilities in dusty plasmas. Planet. Space Sci. 41, 229.Google Scholar
Rosengberg, M. & Krall, N. A. 1996 Low frequency drift instabilities in a dusty plasma. Phys. Plasmas 3, 644.Google Scholar
Rouchoudhury, R. & Mukherjee, S. 1997 Large-amplitude solitary waves in finite temperature dusty plasma. Phys. Plasmas 4, 2305.CrossRefGoogle Scholar
Shahmansouri, M. & Tribeche, M. 2014 Large amplitude dust ion acoustic solitons and double layers in dusty plasmas with ion streaming and high-energy tail electron distribution. Commun. Theor. Phys. 61, 377.Google Scholar
Shukla, P. K. & Mamun, A. A. 2002 Introduction to Dusty Plasma Physics. IOP.Google Scholar
Shukla, P. K. & Silin, V. P. 1992 Dust ion-acoustic wave. Phys. Scr. 45, 508.Google Scholar
Tokar, R. L. & Gary, S. P. 1984 Electrostatic hiss and the beam driven electron acoustic instability in the dayside polar cusp. Geophys. Res. Lett. 11, 1180.Google Scholar
Verheest, F. 1992 Nonlinear dust-acoustic waves in multispecies dusty plasmas. Planet. Space Sci. 40, 1.Google Scholar
Verheest, F., Olivier, C. P. & Hereman, W. A. 2016 Modified Korteweg de-Vries solitons at supercritical densities in two-electron temperature plasmas. J. Plasma Phys. 82 (2), 905820208.Google Scholar
Verheest, F. & Pillay, S. R. 2008 Large amplitude dust-acoustic solitary waves and double layers in nonthermal plasmas. Phys. Plasmas 15, 013703.Google Scholar
Vette, J. I. 1970 Summary of Particle Population in the Magnetosphere, vol. 17, p. 305. Reidel.CrossRefGoogle Scholar