The possibility of a collisionless shock in a plasma not subject to electrostatic instabilities nor immersed in a permanent magnetic field is investigated. The equations governing a steady shock in an electron-ion plasma are deduced and their limitations are discussed. Attention is given to the fact that the velocity distribution in a collisionless plasma may not be Maxwellian. This yields a parameter which is a measure of high-energy particle density. It is found that almost always no steady shock exists. The inverse of the electron plasma wave-number k0=ωp/c provides a scale length for the shock, though the dampening effect of the ions indicates a shock thickness much in excess of 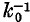. It is concluded that the mechanism for such shocks may be important in a gas such as the solar wind.