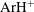Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T10:43:50.121Z Has data issue: false hasContentIssue false
  • English
  • Français

The collision cross-sections for proton–argon interaction based on ab initio$\text{ArH}^{+}$ potential

Published online by Cambridge University Press:  12 March 2020

V. A. Terashkevich Open the ORCID record for V. A. Terashkevich [Opens in a new window] ,
V. V. Meshkov Open the ORCID record for V. V. Meshkov [Opens in a new window] ,
E. A. Pazyuk Open the ORCID record for E. A. Pazyuk [Opens in a new window]  and
A. V. Stolyarov Open the ORCID record for A. V. Stolyarov [Opens in a new window]
V. A. Terashkevich
Affiliation:
Department of Chemistry, Lomonosov Moscow State University, 119991, Moscow, Leninskie gory 1/3, Russia
V. V. Meshkov
Affiliation:
Department of Chemistry, Lomonosov Moscow State University, 119991, Moscow, Leninskie gory 1/3, Russia
E. A. Pazyuk
Affiliation:
Department of Chemistry, Lomonosov Moscow State University, 119991, Moscow, Leninskie gory 1/3, Russia
A. V. Stolyarov*
Affiliation:
Department of Chemistry, Lomonosov Moscow State University, 119991, Moscow, Leninskie gory 1/3, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical collision cross-sections of a proton with an argon atom as well as the thermal transport coefficients and rate constant of the colliding $\text{H}^{+}-\text{Ar}$ system are evaluated at the kinetic temperature 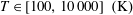$T\in [100,10\,000]~(\text{K})$ by means of the asymptotically correct analytical potential constructed for the ground 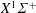$X^{1}\unicode[STIX]{x1D6F4}^{+}$ state of the ArH+ cation from the highly accurate ab initio data available in the entire range of internuclear distances (Terashkevich et al., J. Quant. Spectrosc. Radiat. Transfer, vol. 234, 2019, pp. 139–146). The results can be useful to estimate thermodynamic, transport and kinetic properties of the Ar/H2 plasma in a wide temperature range.

Keywords

plasma properties
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 2 , April 2020 , 905860202
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anicich, V. G. 1993 Evaluated bimolecular ion-molecule gas phase kinetics of positive ions for use in modeling planetary atmospheres, cometary comae, and interstellar clouds. J. Phys. Chem. Ref. Data 22, 1469–1569.CrossRefGoogle Scholar
Banks, P. M. & Kockarts, G. 1973 Aeronomy, Part B. Academic Press.Google Scholar
Bogaerts, A. 2002 Hydrogen addition to an argon glow discharge: a numerical simulation. J. Anal. Atomic Spectrometry 17, 768–779.CrossRefGoogle Scholar
Bogaerts, A. & Gijbels, R. 2002 Hybrid Monte Carlo – fluid modeling network for an argon/hydrogen direct current glow discharge. Spectrochimica Acta Part B: Atomic Spectroscopy 57, 1071–1099.CrossRefGoogle Scholar
Bruno, D., Catalfamo, C., Capitelli, M., Colonna, G., De Pascale, O., Diomede, P., Gorse, C., Laricchiuta, A., Longo, S., Giordano, D. et al. 2010 Transport properties of high-temperature jupiter atmosphere components. Phys. Plasmas 17 (11), 112315.CrossRefGoogle Scholar
Busevica, L., Klincare, I., Nikolayeva, O., Tamanis, M., Ferber, R., Meshkov, V. V., Pazyuk, E. A. & Stolyarov, A. V. 2011 Fourier transform spectroscopy and direct potential fit of a shelflike state: application to E(4)$^{1}\unicode[STIX]{x1D6F4}^{+}$ KCs. J. Chem. Phys. 134 (10), 104307.Google Scholar
Capitelli, M., Bruno, D. & Laricchiuta, A. 2013 Fundamental Aspects of Plasma Chemical Physics: Transport. Springer Science + Business Media.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. 1958 The Mathematical Theory of Non-uniform Gases. Cambridge University Press.Google Scholar
Coxon, J. A. & Hajigeorgiou, P. G. 2016 Accurate internuclear potential energy functions for the ground electronic states of NeH+ and ArH+. J. Molecular Spectroscopy 330, 63–71.CrossRefGoogle Scholar
Hirschfelder, J., Curtiss, C. & Bird, R. 1964 Molecular Theory of Gases and Liquids. Wiley.Google Scholar
Houk, R. S., Fassel, V. A., Flesch, G. D., Svec, H. J., Gray, A. L. & Taylor, C. E. 1980 Inductively coupled argon plasma as an ion source for mass spectrometric determination of trace elements. Analyt. Chem. 52 (14), 2283–2289.CrossRefGoogle Scholar
Jimenez-Redondo, M., Cueto, M., Domenech, J. L. & Herrero, V. J. 2014 Ion kinetics in Ar/H2 cold plasmas: the relevance of ArH+. R. Soc. Chem. Adv. 4, 62030–62041.Google ScholarPubMed
Kihara, T., Taylor, M. H. & Hirschfelder, J. O. 1960 Transport properties for gases assuming inverse power intermolecular potentials. Phys. Fluids 3 (5), 715–720.CrossRefGoogle Scholar
Kimura, T. & Kasugai, H. 2010 Properties of inductively coupled of Ar/H2 plasmas: Experiment and global model. J. Appl. Phys. 107 (8), 083308.CrossRefGoogle Scholar
Li, W., Beard, B. L. & Li, S. 2016 Precise measurement of stable potassium isotope ratios using a single focusing collision cell multi-collector ICP-MS. J. Anal. Atomic Spectrometry 31, 1023–1029.CrossRefGoogle Scholar
Maltsev, M. A., Morozov, I. V. & Osina, E. L. 2019 Thermodynamic Properties of ArH+ and ArH. High Temp. 57 (3), 335–337.CrossRefGoogle Scholar
Mason, J. C. & Handscomb, D. C. 2003 Chebyshev Polynomials. CRC.Google Scholar
Medvedev, A., Meshkov, V., Stolyarov, A. & Heaven, M. C. 2018 Ab initio interatomic potentials and transport properties of alkali metal (M $=$ Rb, Cs) – rare gas (Rg $=$ He, Ne, Ar, Kr, Xe) media. Phys. Chem. Chem. Phys. 20, 25974–25982.CrossRefGoogle ScholarPubMed
Mitchell, J. B., Novotny, O., LeGarrec, J. L., Florescu-Mitchell, A., Rebrion-Rowe, C., Stolyarov, A. V., Child, M. S., Svendsen, A., El Ghazaly, M. A. & Andersen, L. H. 2005 Dissociative recombination of rare gas hydride ions: II. ArH+. J. Phys. B 38 (10), 175.CrossRefGoogle Scholar
Murphy, A. 2000 Transport coefficients of hydrogen and argon/hydrogen plasmas. Plasma Chem. Plasma Proc. 20, 279–297.CrossRefGoogle Scholar
O’Hara, H. & Smith, F. 1971 Transport collision integrals for a dilute gas. Comput. Phys. Commun. 2 (1), 47–54.CrossRefGoogle Scholar
Ostrikov, K. K., Yoon, H.-J., Rider, A. E. & Vladimirov, S. V. 2007 Two-dimensional simulation of nanoassembly precursor species in $\text{Ar}+\text{H}_{2}+\text{C}_{2}\text{H}_{2}$ reactive plasmas. Plasma Proc. Polymers 4 (1), 27–40.CrossRefGoogle Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1999 Numerical Recipes in Fortran, vol. 77. Cambridge University Press.Google Scholar
Rat, V., André, P., Aubreton, J., Elchinger, M. F., Fauchais, P. & Vacher, D. 2002 Transport coefficients including diffusion in a two-temperature argon plasma. J. Phys. D 35 (10), 981–991.CrossRefGoogle Scholar
Shibata, N., Fudagawa, N. & Kubota, M. 1992 Effects of hydrogen mixed with argon carrier gas in electrothermal vaporization-inductively coupled plasma-mass spectrometry. Spectrochimica Acta Part B: Atomic Spectroscopy 47, 505–516.CrossRefGoogle Scholar
Soldan, P., Lee, E. & Wright, T. 2001 Static dipole polarizabilities ($\unicode[STIX]{x1D6FC}$) and static second hyperpolarizabilities ($\unicode[STIX]{x1D6FE}$) of the rare gas atoms (He-Rn). Phys. Chem. Chem. Phys. 3, 4661.CrossRefGoogle Scholar
Stolyarov, A. V. & Child, M. S. 2005 Theoretical study of the ArH+ electronic states. Phys. Chem. Chem. Phys. 7, 2259–2265.CrossRefGoogle ScholarPubMed
Taylor, W. L.1979 Algorithms and FORTRAN programs to calculate classical collision integrals for realistic intermolecular potentials. [Classical transport integrals; SCAN; Coll], doi:10.2172/5842372.CrossRefGoogle Scholar
Terashkevich, V. A., Pazyuk, E. A., Stolyarov, A. V. & Wiebe, D. S. 2019 An accurate ab initio electronic structure calculation for interstellar argonium. J. Quant. Spectrosc. Radiat. Transfer 234, 139–146.CrossRefGoogle Scholar
Troe, J. 1979 Predictive possibilities of unimolecular rate theory. J. Phys. Chem. 83 (1), 114–126.CrossRefGoogle Scholar
Supplementary material: File

Terashkevich et al. supplementary material

Terashkevich et al. supplementary material

Download Terashkevich et al. supplementary material(File)
File 29.4 KB