No CrossRef data available.
Article contents
Characteristics of collisional damping of surface ion-acoustic mode in Divertor Plasma Simulator-2 (DiPS-2)
Part of:
Focus on Fusion
Published online by Cambridge University Press: 15 December 2021
Abstract
The dissipation of ion-acoustic surface waves propagating in a semi-bounded and collisional plasma which has a boundary with vacuum is theoretically investigated and this result is used for the analysis of edge-relevant plasma simulated by Divertor Plasma Simulator-2 (DiPS-2). The collisional damping of the surface wave is investigated for weakly ionized plasmas by comparing the collisionless Landau damping with the collisional damping as follows: (1) the ratio of ion temperature $({T_i})$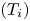
to electron temperature $({T_e})$
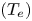should be very small for the weak collisionality $({T_i}/{T_e} \ll 1)$
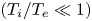; (2) the effect of collisionless Landau damping is dominant for the small parallel wavenumber, and the decay constant is given as $\gamma \approx{-} \sqrt {\mathrm{\pi }/2} {k_\parallel }{\lambda _{De}}\omega _{pi}^2/{\omega _{pe}}$
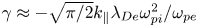; and (3) the collisional damping dominates for the large parallel wavenumber, and the decay constant is given as $\gamma \approx{-} {\nu _{in}}/16$
, where ${\nu _{in}}$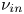
is the ion–neutral collisional frequency. An experimental simulation of the above theoretical prediction has been done in the argon plasma of DiPS-2, which has the following parameters: plasma density ${n_e} = (\textrm{2--9)} \times \textrm{1}{\textrm{0}^{11}}\;\textrm{c}{\textrm{m}^{ - 3}}$
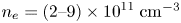, ${T_e} = 3.7- 3.8\;\textrm{eV}$
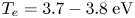, ${T_i} = 0.2- 0.3\;\textrm{eV}$
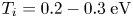and collision frequency ${\nu _{in}} = 23- 127\;\textrm{kHz}$
. Although the wavelength should be specified with the given parameters of DiPS-2, the collisional damping is found to be $\gamma = ( - 0.9\;\textrm{to}\; - 5) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$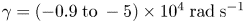
for ${k_\parallel }{\lambda _{De}} = 10$
, while the Landau damping is found to be $\gamma = ( - 4\;\textrm{to}\; - 9) \times {10^4}\;\textrm{rad}\;{\textrm{s}^{ - 1}}$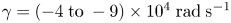
for ${k_\parallel }{\lambda _{De}} = 0.1$
.
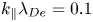- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
Alexandrov, A.F., Bogdankevich, L.S. & Rukhadze, A.A. 1984 Principles of Plasma Electrodynamics. Springer.CrossRefGoogle Scholar
Aliev, Y.M., Schlüter, H. & Shivarova, A. 2000 Guided-Wave-Produced Plasmas. Springer.CrossRefGoogle Scholar
Banks, J.W., Brunner, S., Berger, R.L., Arrighi, W.J. & Tran, T.M. 2017 Collisional damping rates for electron plasma waves reassessed. Phys. Rev. E 96, 043208.CrossRefGoogle ScholarPubMed
Barr, H.C. & Boyd, T.J.M. 1972 Surface waves in hot plasmas. J. Phys. A 5, 1108.CrossRefGoogle Scholar
Claire, N., Bachet, G., Stroth, U. & Doveil, F. 2006 Laser-induced-fluorescence observation of ion velocity distribution functions in a plasma sheath. Phys. Plasmas 13, 062103.CrossRefGoogle Scholar
Girka, V., Girka, I. & Thumm, M. 2014 Surface Flute Waves in Plasmas. Springer.CrossRefGoogle Scholar
Kang, I.J., Bae, M.-K., Lho, T. & Chung, K.-S. 2017 Experimental investigation of free and bounded presheaths in weakly magnetized plasmas. Curr. Appl. Phys. 17, 358.CrossRefGoogle Scholar
Kang, I.J., Bae, M.-K., Park, I.S., Lee, M.J. & Chung, K.-S. 2020 Estimation of plasma density perturbation from dusty plasma injection by laser irradiation on tungsten target in DiPS. Plasma Sci. Technol. 22, 045601.CrossRefGoogle Scholar
Kaw, P.K. & Mcbride, J.B. 1970 Surface waves on a plasma half-space. Phys. Fluids 13, 1784.CrossRefGoogle Scholar
Kumar, N. & Roberts, B. 2003 Ion–neutral collisions effect on MHD surface waves. Solar Phys. 214, 241.CrossRefGoogle Scholar
Leake, J.E., Arber, T.D. & Khodachenko, M.L. 2005 Collisional dissipation of Alfvén waves in a partially ionised solar chromosphere. Astron. Astrophys. 442, 1091.CrossRefGoogle Scholar
Lee, M.-J. & Jung, Y.-D. 2018 Ion-driven instabilities of surface dust ion-acoustic waves in bounded plasma devices. Plasma Sources Sci. Technol. 27, 025010.CrossRefGoogle Scholar
Li, C., Wu, Z., Yang, W. & Chu, P.K. 2014 Surface electromagnetic wave equations in a warm magnetized quantum plasma. Phys. Plasmas 21, 072114.CrossRefGoogle Scholar
Mishra, R. & Dey, M. 2018 Propagation of electrostatic surface wave along the dust void boundary. Phys. Scr. 93, 085601.CrossRefGoogle Scholar
Oksuz, L., Atta Khedr, M. & Hershkowitz, N. 2001 Laser induced fluorescence of argon ions in a plasma presheath. Phys. Plasmas 8, 1729.CrossRefGoogle Scholar
Polo, J. Jr., Mackay, T. & Lakhtakia, A. 2013 Electromagnetic Surface Waves. Elsevier.Google Scholar
Shokri, B. 2000 Low-frequency waves and relaxation processes in semibounded and bounded plasma-like media. Phys. Plasmas 7, 3867.CrossRefGoogle Scholar
Shokri, B. & Rukhadze, A.A. 2019 Electrodynamics of Conducting Dispersive Media. Springer.CrossRefGoogle Scholar
Stenflo, L. 1996 Theory of nonlinear plasma surface waves. Phys. Scr. T63, 59.CrossRefGoogle Scholar
Tigik, S.F., Ziebell, L.F. & Yoon, P.H. 2016 Collisional damping rates for plasma waves. Phys. Plasmas 23, 064504.CrossRefGoogle Scholar
Trivelpiece, A.W. 1967 Slow-Wave Propagation in Plasma Waveguides. San Francisco Press.Google Scholar
Trivelpiece, A.W. & Gould, R.W. 1959 Space charge waves in cylindrical plasma columns. J. Appl. Phys. 30, 1784.CrossRefGoogle Scholar