Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T04:23:50.357Z Has data issue: false hasContentIssue false
  • English
  • Français

Bridging the gap between collisional and collisionless shock waves

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  09 March 2021

Antoine Bret Open the ORCID record for Antoine Bret [Opens in a new window]  and
Asaf Pe'er
Antoine Bret*
Affiliation:
ETSI Industriales, Universidad de Castilla-La Mancha, 13071Ciudad Real, Spain Instituto de Investigaciones Energéticas y Aplicaciones Industriales, Campus Universitario de Ciudad Real, 13071Ciudad Real, Spain
Asaf Pe'er
Affiliation:
Department of Physics, Bar-Ilan University, Ramat-Gan52900, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

While the front of a fluid shock is a few mean-free-paths thick, the front of a collisionless shock can be orders of magnitude thinner. By bridging between a collisional and a collisionless formalism, we assess the transition between these two regimes. We consider non-relativistic, non-magnetized, planar shocks in electron–ion plasmas. In addition, our treatment of the collisionless regime is restricted to high-Mach-number electrostatic shocks. We find that the transition can be parameterized by the upstream plasma parameter 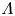$\varLambda$ which measures the coupling of the upstream medium. For 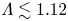$\varLambda \lesssim 1.12$, the upstream is collisional, i.e. strongly coupled, and the strong shock front is about 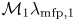$\mathcal {M}_1 \lambda _{\mathrm {mfp},1}$ thick, where 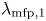$\lambda _{\mathrm {mfp},1}$ and 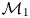$\mathcal {M}_1$ are the upstream mean free path and Mach number, respectively. A transition occurs for 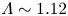$\varLambda \sim 1.12$ beyond which the front is 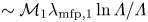$\sim \mathcal {M}_1\lambda _{\mathrm {mfp},1}\ln \varLambda /\varLambda$ thick for 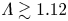$\varLambda \gtrsim 1.12$. Considering that 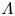$\varLambda$ can reach billions in astrophysical settings, this allows an understanding of how the front of a collisionless shock can be orders of magnitude smaller than the mean free path, and how physics transitions continuously between these two extremes.

Keywords

astrophysical plasmasplasma nonlinear phenomenaspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 2 , April 2021 , 905870204
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baalrud, S. D., Callen, J. D. & Hegna, C. C. 2008 A kinetic equation for unstable plasmas in a finite space-time domain. Phys. Plasmas 15 (9), 092111.CrossRefGoogle Scholar
Bale, S. D., Mozer, F. S. & Horbury, T. S. 2003 Density-transition scale at quasiperpendicular collisionless shocks. Phys. Rev. Lett. 91, 265004.CrossRefGoogle ScholarPubMed
Balogh, A. & Treumann, R. A. 2013 Physics of Collisionless Shocks: Space Plasma Shock Waves. Springer.CrossRefGoogle Scholar
Berezhko, E. G. & Ellison, D. C. 1999 A simple model of nonlinear diffusive shock acceleration. Astrophys. J. 526 (1), 385–399.CrossRefGoogle Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511.CrossRefGoogle Scholar
Biskamp, D. & Pfirsch, D. 1969 Comments on “Turbulent shock waves in plasmas”. Phys. Fluids 12 (3), 732–733.CrossRefGoogle Scholar
Bret, A. 2020 Can we trust MHD jump conditions for collisionless shocks? Astrophys. J. 900 (2), 111.CrossRefGoogle Scholar
Bret, A. & Narayan, R. 2018 Density jump as a function of magnetic field strength for parallel collisionless shocks in pair plasmas. J. Plasma Phys. 84 (6), 905840604.CrossRefGoogle Scholar
Bret, A. & Narayan, R. 2019 Density jump as a function of magnetic field for collisionless shocks in pair plasmas: the perpendicular case. Phys. Plasmas 26 (6), 062108.CrossRefGoogle Scholar
Buneman, O. 1964 Models of collisionless shock fronts. Phys. Fluids 7 (11), S3–S8.CrossRefGoogle Scholar
Chandrasekhar, S. 1943 Stochastic problems in physics and astronomy. Rev. Mod. Phys. 15, 1–89.CrossRefGoogle Scholar
Dupree, T. H. 1966 A perturbation theory for strong plasma turbulence. Phys. Fluids 9 (9), 1773–1782.CrossRefGoogle Scholar
Fitzpatrick, R. 2014 Plasma Physics: An Introduction. Taylor & Francis.CrossRefGoogle Scholar
Gross, E. P. & Krook, M. 1956 Model for collision processes in gases: small-amplitude oscillations of charged two-component systems. Phys. Rev. 102, 511.CrossRefGoogle Scholar
Hammett, G. W. & Perkins, F. W. 1990 Fluid moment models for landau damping with application to the ion-temperature-gradient instability. Phys. Rev. Lett. 64, 3019–3022.CrossRefGoogle ScholarPubMed
Hazeltine, R. D. 1998 Transport theory in the collisionless limit. Phys. Plasmas 5 (9), 3282–3286.CrossRefGoogle Scholar
Kulsrud, R. M. 2005 Plasma Physics for Astrophysics. Princeton Univeristy Press.CrossRefGoogle Scholar
Lee, Y. T. & More, R. M. 1984 An electron conductivity model for dense plasmas. Phys. Fluids 27 (5), 1273–1286.CrossRefGoogle Scholar
Mott-Smith, H. M. 1951 The solution of the Boltzmann equation for a shock wave. Phys. Rev. 82 (6), 885–892.CrossRefGoogle Scholar
Petschek, H. E. 1958 Aerodynamic dissipation. Rev. Mod. Phys. 30, 966–974.CrossRefGoogle Scholar
Ruyer, C., Gremillet, L., Bonnaud, G. & Riconda, C. 2017 A self-consistent analytical model for the upstream magnetic-field and ion-beam properties in Weibel-mediated collisionless shocks. Phys. Plasmas 24 (4), 041409.CrossRefGoogle Scholar
Sagdeev, R. Z. 1966 Cooperative phenomena and shock waves in collisionless plasmas. Rev. Plasma Phys. 4, 23.Google Scholar
Salas, M. D. 2007 The curious events leading to the theory of shock waves. Shock Waves 16 (6), 477–487.CrossRefGoogle Scholar
Schwartz, S. J., Henley, E., Mitchell, J. & Krasnoselskikh, V. 2011 Electron temperature gradient scale at collisionless shocks. Phys. Rev. Lett. 107, 215002.CrossRefGoogle ScholarPubMed
Spitkovsky, A. 2008 Particle acceleration in relativistic collisionless shocks: fermi process at last? Astrophys. J. Lett. 682, L5–L8.CrossRefGoogle Scholar
Stockem, A., Fiuza, F., Bret, A., Fonseca, R. A. & Silva, L. O. 2014 Exploring the nature of collisionless shocks under laboratory conditions. Sci. Rep. 4, 3934.CrossRefGoogle ScholarPubMed
Thorne, K. S. & Blandford, R. D. 2017 Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics. Princeton University Press.Google Scholar
Tidman, D. A. 1958 Structure of a shock wave in fully ionized hydrogen. Phys. Rev. 111 (6), 1439–1446.CrossRefGoogle Scholar
Tidman, D. A. 1967 Turbulent shock waves in plasmas. Phys. Fluids 10 (3), 547–564.CrossRefGoogle Scholar
Tidman, D. A. & Krall, N. A. 1969 Reply to comments by D. Biskamp and D. Pfirsch. Phys. Fluids 12 (3), 733–735.CrossRefGoogle Scholar
Zel'dovich, Y. B. & Raizer, Y. P. 2002 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Dover Publications.Google Scholar