Suffering a loss is a blessing/ 吃亏是福 – Zheng Banqiao/郑板桥 (1693–1765)
The human superpower is really based on fiction. – Yuval Noah Harari
How does one make a choice among options? The following anecdote from The Three-Character Classic (三字经) illustrates a choice that may be different from yours:
In the Eastern Han Dynasty, there lived a person named Kong Rong. He had five older brothers and one younger brother. One day, his father bought some pears, deliberately picking one of the largest and giving it to Kong Rong. However, Kong Rong shook his head and selected the smallest one.
The logic of little Kong Rong’s choice is not isolated to this case only. Such a choice is frequently exemplified in Western and Eastern cultures. Some examples include the Italian proverb, “He who eats pears with his master should not choose the best”.
Giving away the bigger pear (i.e. not to make a value-maximizing choice) is understood as incurring costs to allocate benefits to others. This choice of human generosity is illogical according to economic rationality models (Delton, Krasnow, Tooby, & Cosmides, Reference Delton, Krasnow, Tooby and Cosmides2011). For example, in classical decision theory, options are presented as points in a multidimensional space, in which each dimension represents a distinct attribute that describes the object (Birnbaum, Reference Birnbaum1997; S. Li, Reference Li2004, Reference Li2016; Méndez, Reference Méndez1974). Importantly, in some decision models such as INdividual Differences SCALing (INDSCAL; Carroll & Chang, Reference Carroll and Chang1970), an important aspect is the dimensional uniqueness property, that is, its dimensions are unique (Carroll & Arabie, Reference Carroll, Arabie and Birmbaum1998). When options are represented by a fixed set of dimensions in such models, choices are assumed to be guided by the principle of value maximization (VM) (Luce, Reference Luce1959). Each option x is assigned a value v(x), such that the decision maker selects the option with the highest value in the face of a given set of dimensions (Tversky & Shafir, Reference Tversky and Shafir1992).
In light of these models and their assumptions, the father of little Kong Rong or bystanders will come to a deadlock. In other words, little Kong Rong’s choice is a dominated option. The value (or any extended form of utility, such as predicted utility, experienced utility, decision utility, prospective utility and many others) assigned to the selected option (the smallest pear) should in no way be greater than that assigned to the unselected option (the bigger pear). This premise holds true as long as the choices are restricted to the options offered by the father of little Kong Rong, and the value is limited to a given biological dimension (representing the option as a small or big pear) on which any type of utility is to be established.
Does the choice of a dominated option, which contradicts the VM principle, represent a decision bias or a deliberate decision? If choosing a dominated option is not a bias or error (e.g. a decision by an individual with mental incapacity), then how can the deadlock be resolved? Similar to when the deadlock of “irrational” altruism can be resolved by understanding the manner in which “altruism is actually selfishness in disguise” (Fisher, Reference Fisher1999, p. 151; see also Hamilton, Reference Hamilton1964; Hu, Li, Jia, & Xie, Reference Hu, Li, Jia and Xie2016; X. Li, & Xie, Reference Li and Xie2017; Trivers & Hare, Reference Trivers and Hare1976), we believe that something has not been captured by traditional theories of choice that can help explain why the dominated option is frequently selected by ordinary people.
In the context of the little Kong Rong example, the deadlock remains undetected even if little Kong Rong explains his rationale for choosing a small pear over a big pear:
His dad was very curious and asked, “Why?” Kong Rong said, “I am younger, so I should eat the smaller pear, and brothers should eat the bigger ones.” His dad was very glad after hearing his words but asked further, “What about your younger brother who is younger than you are?” Kong Rong said, “I am older than him, so, I should leave the bigger one to my little brother.”
Neither younger nor older person should choose the bigger pear, which means that Kong Rong should consistently pick the smallest one all his life. Kong Rong’s explanation illustrates the manner in which the mechanisms of choice that fail to maximize the values of the offered options remain largely undefined.
To address this gap in understanding, we propose and demonstrate a “worth-based choice” approach, as compared to a “value-based choice” approach, to explain and predict choices that result in apparent loss (e.g. Tang, Zhou, Zhao, & Li, Reference Tang, Zhou, Zhao and Li2014; Zhao et al., Reference Zhao, Shen, Rao, Zheng, Liu and Li2018). In classical analysis, the relationship of preference is inferred from observed responses and is assumed to reflect the decision maker’s underlying utility or value (Tversky, Sattath, & Slovic, Reference Tversky, Sattath and Slovic1988). In our proposed model, we define a set of dimensions offered by proposer as x to represent different attributes that describe the options we choose from. Importantly, considering the fictional ability of human decision makers, we define an extra set of dimensions, xc, that is, that are not passively offered by proposer but actively and creatively produced by the decision maker to fictionally present the offered option per se.
Correspondingly, for each option that is represented by a fixed set of dimensions, x, we define a general cardinal utility function, (Uv), v(x), as the value that individuals attach to the various outcomes of the option; for each option that is represented by an extra set of fictional dimensions, xc, we also define a general cardinal utility function, (Uw), w(xc), as the worth, which provides a general metric for measuring the value that individuals attach to the consequences of various outcomes.
After an extra dimension is regenerated and a utility is assigned, the choice between a bigger or smaller pear is viewed as a contest between v(x) and w(xc), which are assigned to these options. In particular, the final choice depends on the utility of v(x) assigned to the options (e.g. pears) on the given dimension. It also depends on the utility of w(xc) assigned to the options on the extra dimension defined above. The decision maker selects the option with the highest worth rather than the one with the highest value.
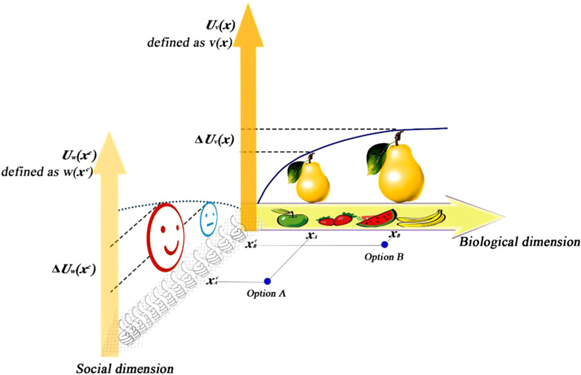
The aim of this study is to examine whether worth-based choice exists and investigate whether a decision maker’s capacity to generate an extra fictional dimension to represent the outcome(s) of the offered options is a key enabler in choosing options with less value. For the remainder of the article, we refer to v(x) and w(xc) as the value and worth associated with the choice respectively. To elaborate the relationship between v(x) and w(xc), we reconsider little Kong Rong’s choice between a smaller pear and a bigger pear (see Figure 1). In the language of our model, both v(x) and w(xc) are the utility of the offered pear options. They differ in that v(x) is the utility (Uv) assigned by Kong Rong to a smaller pear or bigger pear that is represented on the biological dimension, whereas w(xc) is the utility (Uw) assigned by Kong Rong to the option that is represented on an extra fictional dimension of social reinforcement that is not offered by the proposer but is only imagined and produced by Kong Rong thereafter. In this manner, the deadlock is resolved: Kong Rong chooses the pear of less value not because it has greater utility, (Uv), established on the given biological dimension but because it has greater utility, (Uw), established on the newly generated dimension of social reinforcement.
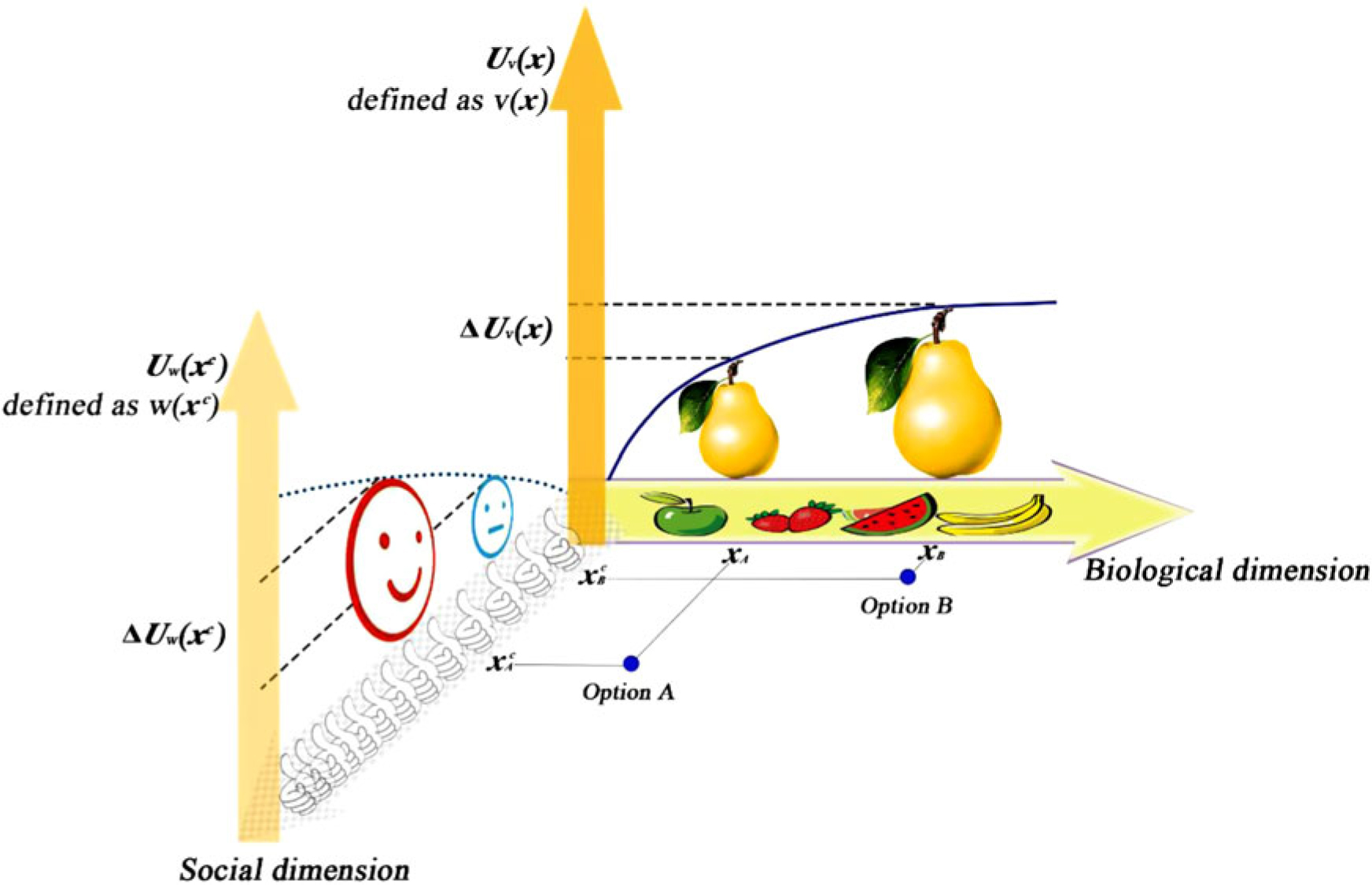
Figure 1. Choice between Option A (smaller pear) and Option B (larger pear) represented as points in a multidimensional space, in which each dimension represents a distinct attribute that describes the object. For ordinary children, the given (offered) dimension that presents the two options is the biological dimension x, in which a smaller pear (Option A) is presented as xA and a larger pear (Option B) as xB. The utilities (Uv) assigned by children to xA and xB on the biological dimension are defined as value, v(x), v(xA) and v(xB), respectively. Grounding their choice on value function, they prefer to choose the larger pear because v(xB) > v(xA). Subsequently, the decision stops. However, Little Kong Rong does not end with maximizing value on the given dimensions between options but continues to generate a new fictional dimension (a social dimension) xc, in which Option A (a smaller pear) and Option B (a bigger pear) can be presented as xAc (with social reinforcement) and xBc (without social reinforcement) respectively. The utilities (Uw) assigned by Kong Rong to xAc and xBc on the social dimension are defined as worth, w(xc), w(xAc) and w(xBc) respectively. The judgment that ΔUw (xc) >> ΔUv (x) will compel Kong Rong to base his choice only on worth function. Thereafter, he selects a smaller pear because w(xAc) > w(xBc).
From the perspective of utility analysis, our model shares a common aspect with existing decision models: people assess the utility of outcomes rather than the outcomes per se. This explanation is the case if utility is treated as a general concept for measuring the value that individuals attach to the consequences of various outcomes, and it can be anchored either in the hedonic experience of outcomes or in the preference or desire for the said outcomes (Kahneman, Reference Kahneman1994). Despite this commonality, previous investigations differ from the present study in that the latter assumes that the utility of outcomes can be assigned to a set of dimensions that are not offered by the proposer but generated by the decision maker in our model; in existing decision models, the utility of outcomes is assigned strictly to a fixed set of dimensions offered by the proposer. We believe that adaptive individuals (a) are rarely satisfied by passively choosing between the utilities assigned to the fixed set of dimensions, (b) will actively generate an extra dimension with fiction, and (c) will assign a utility to the generated dimension in terms of worth. In our view, actors who are willing to go “one step further” do not necessarily arrive accidentally at a value-maximizing level (e.g. S. Li, Reference Li1995, Reference Li1996) but instead reach a choice that ends at a worth-maximizing level. As a consequence, well-adapted individuals in evolving populations make more “one step further” choices than poorly adapted individuals.
In summary, if a decision maker only assesses the outcome of the option based strictly on the fixed set of dimensions that are offered by the proposer, then the utility (Uv) that he/she assigns is defined as v(x). However, if a decision maker further assesses the outcome of the option based on an extra set of dimensions that are created by the decision maker, then the utility (Uw) that he/she assigns is defined as w(xc). The significance of w(xc) is most unlikely to be noted or captured by traditional theories of choice. The distinction between v(x) and w(xc) opens new avenues for the study of choices that result in selecting options with less value. Through extrapolation, the principle of VM can be hypothesized as practiced only if the final decision is ultimately based on the fixed set of dimensions that are offered by the proposer; however, this premise is not necessarily the case when an extra set of dimensions is created to present the outcome of the option. Whether or not an individual is able to creatively produce an extra fictional dimension to represent the outcome(s) of the offered options is a key enabler in making a worth-based choice. The subsequent experiments demonstrate our attempt to prove or disprove our hypothesis regarding the alleged “worth-based choice”.
Experiment 1. Is giving away the larger pear a myth or reality?
Before testing our hypothesis, we intend to ensure that the choice of giving away the larger pear exists in the real-world setting. That is, we aim to replicate the choices established in The Three-Character Classic (三字经) and the Italian proverb: when faced with a choice between a bigger value option and a smaller value option, some people might not make a value-maximizing choice. Giving away the larger pear could be argued as simply explained by the fact that the decision maker does not like pears or something similar to that reason (e.g. not choosing a bigger high-protein hamburger or a bigger high-calorie chocolate might be simply due to the fear of gaining weight). To rule out this concern, we use real common currency (i.e. monetary payoffs) rather than real pears as our choice options in the present experiment because people rarely intend to take a smaller amount of money (S. Li, Bi, Su, & Rao, Reference Li, Bi, Su and Rao2011).
Participants
A total of 62 undergraduate students (24 males, 37 females) from the School of Transportation, Fujian University of Technology participated in this experiment.
Method
Materials and procedure
The participants were recruited to visit the lab twice with an interval of seven days to participate in two unrelated experiments on intertemporal choice. Each experiment lasted for nearly an hour. The facilitators of the experiments were three students and one lecturer from the same school (School of Transportation, Fujian University of Technology). At the end of the second experiment, a fifth experimenter gave each participant the following face-to-face instruction: To thank you and the experimenters (either a fellow student or a lecturer) for joining these time-consuming experiments, you are offered a choice between a larger (Ұ10) or a smaller (Ұ5) Red Packet (红包) as a reward. The not-chosen Red Packet will be left to one of the four experimenters (either a fellow student or a lecturer). The four experimenters were absent in the experiment room when participants made the choices. Participants could recognize the denominations of the paper currency, which was half enveloped in the Red Packet. The participants’ decisions about which option (envelope with ¥5 or envelope with ¥10) to consider were recorded.
The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences. Given that the protocol was judged to pose low risk with the data analyzed anonymously, verbal consent was recommended and obtained from the study participants prior to data collection.
Results and Discussion
Table 1 summarizes the participants’ choice between the two Red Packets.
Table 1. A summary of the measured data. The total number and corresponding percentage of participants (in parentheses) who chose each option as function of the status of experimenter
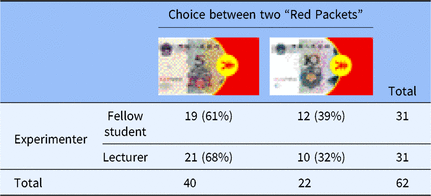
The majority of our participants (64.5%) appeared to have behaved consistently with those reported in The Three-Character Classic (三字经) and the Italian proverb: 40 out of the 62 participants selected the smaller amount of monetary payoff (c.f. smaller pear), χ2(1, N = 62) = 5.226, p = .022, phi-squared = 0.290. More participants selected “red packets with ¥5” under the lecturer condition (68%) compared with those under the fellow student condition (61%). However, the difference did not reach statistical significance, χ2(1, N = 62) = 0.282, p = .596, phi-squared = 0.067.
Our finding suggests that the choice of selecting the option with less value (in terms of giving away the bigger pear) is not a myth but a certain reality. The experimental design, which used real monetary payoffs as the choice options, could rule out the possibility that the choice of selecting the option with less value was a result of practicing the principle of value minimizing (e.g. taking a smaller low-calorie chocolate to keep fit). The following experiment sought to answer the question of what participants were maximizing if they did not maximize the outcomes on the offered monetary dimension. In the language of worth-based choice, we attempted to determine what unoffered non-monetary dimension participants were maximizing.
Experiment 2. In whose eyes is the lower value always lower and less attractive, children’s or parents’?
To test our hypothesis, we then compared the decisions of children with those of their parents. The lack of any hidden meanings in the options offered to the children allows us to manipulate the presence of generated dimensions by selecting participants from different generations. In other words, in addition to the given set of dimensions offered by the proposer, the parental generation can possibly generate an additional dimension(s) that the children’s generation cannot.
Methods
Preliminary investigation
To identify a dimension that children cannot possibly generate, we first consider numbers and colors that are nominal scales in terms of “economic value” but mean different things to different people in different cultures (Block & Kramer, Reference Block and Kramer2009; Hutchings, Reference Hutchings2004; Sutton & Whelan, Reference Sutton and Whelan2004; Wiseman & Watt, Reference Wiseman and Watt2004). For example, in the English culture, 13 is an unlucky number, whereas in the Chinese culture, 13 is not unlucky, but 4 is unlucky (Lin, Reference Lin2004). For the Chinese, the color red means happiness; for the Japanese, it means anger or danger; for Egyptians, it means death; for the French, it means aristocracy; and for Americans, it means danger or stop (Al-Badi & Mayhew, Reference Al-Badi and Mayhew2010).
We therefore constructed 10 phone numbers (from 510 to 519) and eight colored lanterns (the seven colors of the rainbow plus white). Twenty 3- to 6-year-old Chinese children (11 females, mean year = 4.70, SD = 0.86) in the local community in Beijing were asked to ascertain any meaning behind a phone number or colored lantern. If the answer was negative, then no other question was asked. If the answer was positive, then the children were asked about the meaning.
When asked the phone number question, all of the children recognized the numbers without difficulty, but none of them (0%) could decipher a meaning behind the 10 phone numbers. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
In the questions about the colored lanterns, 16 children (80%) failed to decipher a meaning behind the eight colored lanterns. Only four children (20%) reported that they had observed red/orange lanterns during the Spring Festival. However, they could not explain what red/orange represented.
The result suggested that 3- to 6-year-old children have not yet acquired the representative meanings of phone numbers or colored lanterns from their culture’s customs. Considering that the meanings of numbers and colors vary depending on their context in Chinese customs and culture, we specifically used “red and white lanterns” and “514Footnote 1 and 518Footnote 2 phone numbers” as the options’ outcomes, which are fictionally represented by generated dimensions for adults in the scenarios of Experiment 2.
Participants
Participants were recruited through word-of-mouth and messages posted in three kindergartens in Jinan, China. Children were asked whether they, together with their parents, would have fun by making some choices. Twenty-nine mother–daughter dyads and 31 father–son dyads (children’s age range = 3–6 years; parents’ age range = 27–36 years) at the three kindergartens were approached to participate in the study. All of our participants were Chinese. These subjects were selected randomly and were paid 10 Yuan for participating.
Materials and procedure
A colored lantern scenario and a mobile phone number scenario were constructed to produce VM data. Each scenario contained three pairs of choices (which differed only in the bracketed text) between a relatively economical or cheap lantern or phone number (Ұ10) and a relatively expensive one (Ұ20), which read as follows.
Mobile phone number scenario: Suppose you were to buy a mobile phone number. Being faced with only two options, which would you prefer?
A. A mobile phone number ending with 513 (513/514) at the price of Ұ10
B. A mobile phone number ending with 517 (518/517) at the price of Ұ20
Colored lantern scenario: Suppose you plan to buy a lantern for the New Year. Faced with only two options, which would you prefer?
A. A blue (blue/white) lantern at the price of Ұ10
B. A purple (red/purple) lantern at the price of Ұ20
The choices presented to the children were enlarged photos with real paper money. One-third of the parent–child dyads were randomly assigned to each of the three pairs of choices. The children and their parents were asked separately to indicate which option out of each pair they preferred and how strongly they preferred it (for children: one smiley face indicated that the choice was slightly preferred; two smiley faces indicated that the choice was preferred; and three smiley faces indicated that the choice was strongly preferred). As a result, a variable called “strength of preference” was constructed: “strongly prefer A” was coded as 1, “prefer A” was coded as 2, “slightly prefer A” was coded as 3, “slightly prefer B” was coded as 4, “prefer B” was coded as 5, and “strongly prefer B” was coded as 6.
After completing the hypothetical decisions, each participant was asked to choose between a larger (Ұ6) or a smaller (Ұ3) Dove Chocolate Singles Bar as a reward or gift for the participant as well as the experimenter, and the participant’s selection was recorded.
Results and discussion
In the recorded chocolate selections, 93.3% of the children chose the bigger Dove Chocolate Singles Bar, whereas only 8.3% of their parents made the same choice, χ2(1, N = 120) = 86.72, p < .001, phi-squared = .72. The choice of the smaller pear prescribed in Western and Eastern cultures is perfectly reflected in the decisions of cultivated parents.
Table 2 summarizes the percentages (and actual numbers) of participants who chose each option in the two scenarios. A 2 (generation) × 3 (pair) × 2 (scenario, nested within participants) analysis of variance (ANOVA) conducted on the strength of preference revealed a significant main effect of generation, F(1, 114) = 113.69, p < .001, and a significant main effect of pair, F(2, 114) = 32.58, p < .001. No significant effect of scenario was found, F(1, 114) = .23, p = .63. Similarly, no significant interaction effects were found between generation and scenario, F(1, 114) = .03, p = .87, or between pair and scenario, F(2, 114) = .08, p = .93. However, a significant interaction effect was found between generation and pair, F(2, 114) = 22.78, p < .001.
Table 2. A summary of the measured data: Means of the strength of preference, the total number (in parentheses) and corresponding percentage of participants who chose each option as functions of the scenario and the choice pair
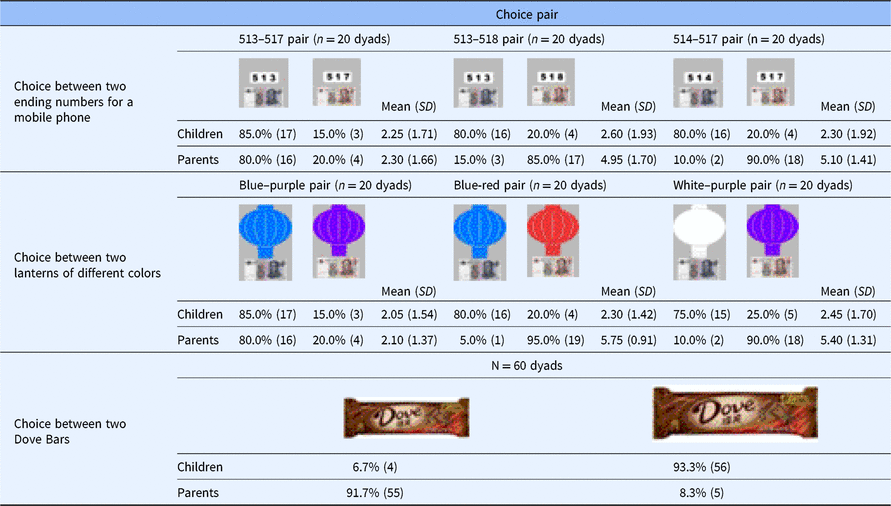
When faced with the colored lantern and mobile phone number scenarios, the children always chose the options with the greater value (more economical or cheap) regardless of the competing option (all means for strength of preference ≤ 2.60), and no significant difference was found between pairs, F(2, 57) = 0.42, p = .66. Their overwhelming choices suggest that the option with the greater value is dominant. When a dominant option exists, it is unambiguously the best option available, and therefore no further analysis is required (von Winterfeldt & Edwards, Reference von Winterfeldt and Edwards1986). However, our parent participants behaved differently across pairs; a significant main effect existed for pairs, F(2, 57) = 66.50, p < .001. They chose the options with greater value (more economical or cheap) when the competing option was a phone number ending with 517 (M 513-517 pair = 2.30) or the purple lantern (M blue-purple pair = 2.10) and chose the options with less value (more expensive) when the competing option was the phone number ending with 513 (M 513-518 pair = 4.95)/blue lantern (M blue-red pair = 5.75) or the phone number ending with 514 (M 514-517 pair = 5.10)/white lantern (M white-purple pair = 5.40).
Overall, the paired results showed that the stern practitioners of the principle of value maximization were not the parents but their children. The observed generation gap is robust even if the choice is between real and non-evocative items. Our explanation for this phenomenon is that adults have generated a fictional dimension, assigned a utility (worth) to the options on the fictional dimension, and maximized the utility (worth) thereafter. We consider the resulting findings (i.e. children failed to decipher the meaning behind the numbers and colors) as supportive evidence that children were unable to automatically generate a fictional dimension (consequently, they can only maximize value on the offered monetary dimension). Notably, the number of attributes (monetary + color/number) that describes the offered options in the present experiment was more than that (monetary only) in Experiment 1. The additional attribute of color or number provided by the options themselves could be argued to be relevant to the so-called fictional dimension (auspiciousness dimension), thereby possibly leading people to question whether the so-called non-monetary dimensions were not offered but the one actually generated by the decision makers themselvesFootnote 3. Therefore, the following experiment sought to collect other evidence to support our conjecture that fictional ability other than providing a related attribute is a must to generate a fictional dimension. In particular, the following experiment sought to answer why a dominant option in the eyes of a child might turn out to be a non-dominant option in the eyes of an adult. That is, which aspects render a bigger pear insufficiently large to be chosen?
Experiment 3a. When choosing options with unknown/unrealistic source, what are the concepts that are seen and represented on generated dimension(s)?
When faced with a choice between colored lanterns or between mobile phone numbers, which are supposed to mean different things to different people in different cultures, our parent participants in Experiment 2 tended to choose the option with less value. The present experiment aimed to identify the aspects that are fictionally represented on generated dimension(s), thereby prompting adults to choose the option with less value.
Participants
This experiment was performed with college students only. Participants were 148 Chinese undergraduate students from the Central University of Finance and Economics who were recruited through advertisements posted on the university campus in Beijing. All of the participants provided informed consent and were paid for their participation. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
Method
Materials and procedure
In the present experiment, the thought-listing procedure suggested by query theory (Johnson, Häubl, & Keinan, Reference Johnson, Häubl and Keinan2007) was used. The basic assumption of this approach is that when agents are faced with a decision, they generally decompose the overall question into a series of component queries. The order of these queries is shaped by one’s implicit goals in the situation. As a result of each query, various aspects of the situation are recruited from memory in a serial manner. The method suggested by query theory is supposed to know the things we want by arguing with ourselves (Weber & Johnson, Reference Weber and Johnson2011); moreover, it has been used successfully in analyzing cognitive processes in similar tasks (Hardisty, Johnson, & Weber, Reference Hardisty, Johnson and Weber2010; Johnson et al., Reference Johnson, Häubl and Keinan2007; Weber et al., Reference Weber, Johnson, Milch, Chang, Brodscholl and Goldstein2007). Participants first performed a choice task using the same mobile phone number and colored lantern scenarios as those in Experiment 2. Thereafter, they practiced listing their thoughts by describing the reasons for their choices and by answering the following prompt: “Please provide at least two reasons for this decision.”
Results and discussion
Student participants in the present experiment made choices similar to those of the parent participants in Experiment 2. The presence of sequential queries and the order of these queries can be inferred from a statistic known as the standardized median rank difference (SMRD; see Johnson et al., Reference Johnson, Häubl and Keinan2007). We computed the SMRD scores of the respondents in different pairs using the SMRD formula. SMRD was defined as 2(MRi – MRd)/n, where MRd = median rank of the offered monetary aspects in a participant’s sequence, MRi = median rank of the generated nonmonetary aspects in a participant’s sequence, and n is the total number of aspects listed. For any sequence (of length s) in which only one of the two response categories of interest (i.e. non-monetary aspects or monetary aspects) appears, the median rank of the unobserved response category is set to s + 1, which is a conservative approach for representing the low level of accessibility of thoughts of that type. In addition, for the purpose of calculating the SMRD score, n = s + 1 for such single-category sequences. For sequences that include responses from both categories, n = s. Prior to indicating their valuation of the mobile phone number and the colored lantern, participants listed the aspects they were considering in making their decisions. Specifically, they were instructed to write down all of the reasons why they personally would want to either have the cheap one or the expensive one, providing one reason at a time (see Johnson et al., Reference Johnson, Häubl and Keinan2007). SMRD scores can take values from 1 (all generated non-monetary aspects were listed before any offered monetary aspects) to −1 (all offered monetary aspects were listed before any generated non-monetary aspects; see Table 3).
Table 3. Classification of aspects based on focus and valence

Note: The top left and bottom right cells have non-monetary aspects. The top right and bottom left cells have monetary aspects.
1 Commercial and research interests have invested in number 8. Its application was advertised by Continental Airlines as “$888 to Beijing. Lucky You” before the Beijing Summer Olympics, which were scheduled to begin on August 8, 2008, at 8 p.m. (Kramer & Block, Reference Kramer and Block2008). Not surprisingly, a Chinese airline paid 2.4 million yuan for the telephone number 8888 8888 (Yardley, Reference Yardley2006).
2 “Four” sounds like the word for “death” in Chinese. Using hedonic price analysis, Bourassa and Peng (Reference Bourassa and Peng1999) demonstrated that lucky house numbers are capitalized into house values in Auckland, New Zealand. Because of the stigma associated with the number four, it appears that Chinese households may avoid purchasing houses with that number.
When practicing the principle of VM (means of strength of preference: M 513–517 pair = 1.82; M blue–purple pair = 2.32), the mean SMRD scores for the 513–517 and blue–purple pairs were −0.63 and −0.39 respectively, suggesting that the reasons listed earlier by adult decision makers were limited to monetary aspects (cf. the top right and bottom left cells in Table 3).
When participants were not practicing the principle of VM (means of strength of preference: M 513–518 pair = 4.44; M blue–red pair = 5.52 and M 514–517 pair = 4.67; M white–purple pair = 5.08), the mean SMRD scores fell into the range between 0 and 1 (the mean SMRD scores for the 513–518, 514–517, blue–red, and white–purple pairs were 0.25, 0.26, 0.64, and 0.46 respectively), suggesting that the reasons listed earlier by the adult decision makers were limited to non-monetary aspects (cf. the top left and bottom right cells in Table 3).
The analyses revealed that the mean SMRD scores were significantly higher when participants did not practice the principle of VM than when they practiced such a principle (all Fs ≥ 40.70, ps < .001), with no significant differences between the two pairs in which participants did not practice the principle of VM; the 513–518 pair versus the 514–517 pair, F(1, 96) = 0.01, p = .92; the blue–red pair vs. the white–purple pair, F(1, 96) = 3.45, p = 0.07. Logistic regressions that considered SMRD scores accounted for 83% and 67% of the variance in the choices in the mobile phone number scenario (β = 6.25, p < .001; Nagelkerke R 2 = .83) and in the lantern scenario (β = 3.99, p < .001; Nagelkerke R 2 = .67) respectively.
Thus, the generated dimensions (aspects) produced by the adult decision makers who listed reasons that relatively earlier indicated non-monetary aspects are likely the reasons they chose the option with less value. By contrast, being unable to foresee or turning a blind eye to these additional dimensions may lead to a choice that remains engaged in maximizing values of the offered options. These “query” results and those of Experiment 2 indicate that providing a related attribute (e.g. color or number) is not a must to generate a fictional dimension (e.g. auspiciousness). However, the fictional ability to decipher a meaning behind the offered color or number is a requirement. This ability renders a larger pear insufficient to be chosen.
Experiment 3b. When choosing options with a known/realistic source, what are the concepts that are seen and represented on generated dimension(s)?
When asked to choose between a larger and a smaller Dove Chocolate Singles Bar that is a real, non-superstitious item, our parent participants in Experiment 2 also chose the option with less value. As is implied in the proverb about giving away the bigger pear, the cultural context in such a case might be perceived as a social relationship of whether the unchosen option is specified for a person (e.g. the experimenter in Experiments 1 and 2, the master in the Italian proverb, or the brothers to whom Kong Rong leaves the bigger pear) or not. Therefore, Experiment 3b intended to examine whether the social relationship regarding the not-chosen options being specified for a person or not could enable our participants to choose the option with less value and, if this case was true, to identify the aspects fictionally represented on the generated dimension(s) that could prompt adults to choose the option with less value.
Participants
Experiment 3b was also performed with college students only. A total of 171 Chinese undergraduates and postgraduates (age range = 18–24 years; 62 females) from Beijing Forestry University and the University of Chinese Academy of Sciences participated in this experiment, recruited through advertisements posted on campus billboards in Beijing. All of the participants provided informed consent and were paid for their participation. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
Materials and procedure
Two pairs of choice problems were prepared. Our participants were instructed to respond under two conditions. Under one condition (the not-chosen option not specified for a person), the following instruction was given: “Two options are available for you to choose from.” Under the other condition (the not-chosen option specified for a friend), the following instruction was given: “Two options are available for you and your friend to choose from (i.e. you select A and then your friend gets B; you select B and then your friend gets A).”
Each condition contained two pairs of choices, which reads as follows:
Pencil choosing problem with one option superior in variety:
A. Select one pencil from two pencils in black color
B. Select one pencil from one pencil in white color and one pencil in black color
Pencil choosing problem with one option superior in number:
A. Select one pencil from two pencils in black color
B. Take two pencils from two pencils in black color
Participants were first asked to indicate “which option they would prefer to have” on a 6-point scale (1 = strongly prefer A; 2 = prefer A; 3 = slightly prefer A; 4 = slightly prefer B; 5 = prefer B; 6 = strongly prefer B) under both conditions. Thereafter, under the condition of the not-chosen options being specified for a friend, the participants were asked to write down (as many as possible) their answers to the question “How would you benefit from choosing Option A?” after they had decided on each pair of choices.
Results and discussion
When choosing under the condition in which the not-chosen option was not specified for a person, participants tended to have a stronger preference for Option B, which was superior either in variety (M v = 4.05) or number (M n = 3.76). When choosing under the condition in which the not-chosen option was specified for a friend, their preference decreased for Option B, which was superior in variety (M v = 3.22) or number (M n = 3.26) (see Figure 2).
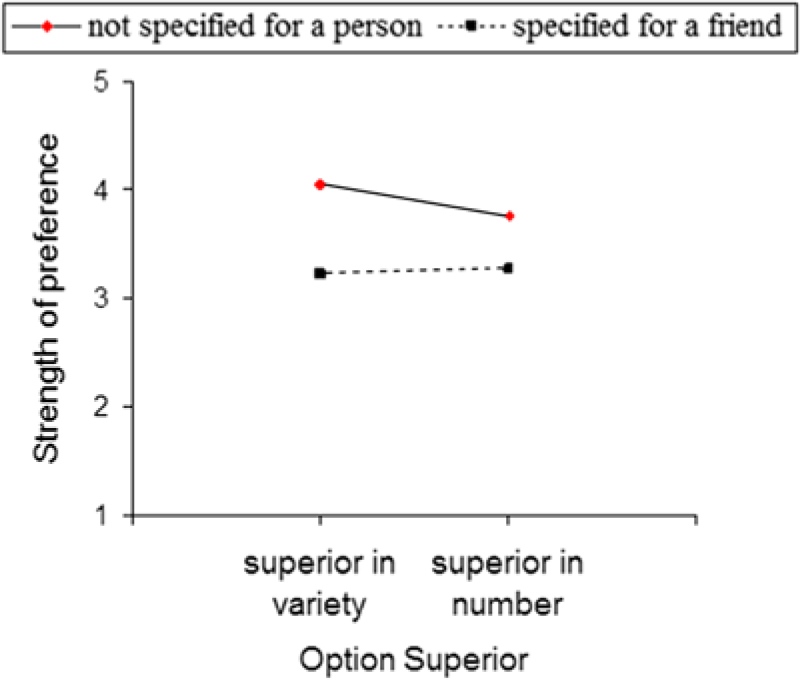
Figure 2. Strength of preference as a function of the not-chosen option (not specified for a person vs. specified for a friend) and the option superior (superior in variety vs. superior in number). The higher the strength of preference score, the more strongly participants prefer Option B (superior in variety or number).
A 2 (not-chosen option: not specified for a person vs. specified for a friend) × 2 (option superior: superior in variety vs. superior in number) ANOVA conducted on the strength of preference revealed a significant main effect of choosing the not-chosen option, F(1,169) = 23.359, p < .01. No significant effect of option superior emerged, F(1, 169) =.793, p = .374. Similarly, no significant interaction effect emerged between not-chosen option and option superior, F(1, 169) = 1.409, p = .236. These findings suggested that the presence of a social relationship regarding the not-chosen option being specified for a person could enable our participants to choose the option with less value.
Table 4 summarizes the participants’ answers to “How would you benefit from choosing Option A?” A total of 433 items rated “benefit” were recorded, with each participant contributing 2.53 items on average. The most frequently indicated benefits included “making my friend happy” and “developing and maintaining friendship” (34.6% and 22.9% in the pair with superiority in variety and 36.1% and 25.5% in the pair with superiority in number respectively). Two major conclusions can be drawn from the findings presented in Table 4. One is that people are indeed able to generate “additional” benefits regardless of whether they have actually selected Option A or not. Those generated benefits can be coded as: (a) leaving Option B to friends makes them happy; (b) less effort is required to make the decision; (c) choosing from two black pencils feels nice; and (d) less is better. The other conclusion is that those who selected Option A generated more “benefits” (M v = 1.64; M n = 1.51) than those who selected Option B (M v = 1.24; M n = 0.74), t = 3.376, p < .01 for the problem with one option superior in variety and t = 5.879, p < .01 for the problem with one option superior in number, suggesting that participants’ abilities to produce additional fictional dimensions (aspects) to represent “benefits” were very likely responsible for their selection of the options with less value.
Table 4. Number of “benefits” listed by the participants for option a under the “not-chosen options being specified for a friend” condition

In summary, these findings consistently provided evidence that the fictional ability and not the presence of the related attribute could enable our participants to generate a fictional dimension and choose the option with less value. What our participants were maximizing is the imagined outcomes on the unoffered non-monetary dimension. Experiments 3a and 3b showed that for those who chose the option with less value, the aspects fictionally represented on the generated dimension(s) by the participants all related to something that had been socialized into their culture. These sociocultural matters count and prompt adults to choose the option with less value. The difference lies in the fact that the aspect fictionally represented on the generated dimension(s) is created by an unknown/unrealistic source (i.e. superstitious beliefs) in Experiment 3a but by a known/realistic source (i.e. a friend) in Experiment 3b.
Experiment 4. How do we stop and reach a final choice? A contest between utilities established on a given dimension and utilities established on a generated dimension
The adults’ contingent responses in the above experiments suggest that the more economical or cheap options are not necessarily the dominant ones. One option is better based on a monetary attribute, whereas the other option is better based on a non-monetary attribute.
In choosing between non-dominant options, an alternative mode is to “equate” the conflicting dimensional differences to render the applicability of a weak dominance rule. Weak dominance states that if option A is at least as good as option B on all attributes, and if option A is definitely better than option B on at least one attribute, then option A dominates option B (c.f. Lee, Reference Lee1971; von Winterfeldt & Edwards, Reference von Winterfeldt and Edwards1986). Considering the limited computational capacity of human decision makers, the equate-to-differentiate model (S. Li, Reference Li1994, Reference Li2001a, Reference Li2001b, Reference Li2003, Reference Li2004, Reference Li2005, Reference Li2006) and the graph-edited, equate-to-differentiate model (Sun, Li, Bonini, & Su, Reference Sun, Li, Bonini and Su2012) postulate that in using the very intuitive or compelling rule of weak dominance to reach a binary choice between option A and option B in more general cases, the final decision is based on detecting option A dominating option B if at least one j exists, such that UAj (xj) – UBj (xj) > 0 having subjectively treated all UAj (xj) – UBj (xj) < 0 as UAj (xj) – UBj (xj) = 0, or detecting option B dominating option A if there exists at least one j, such that UBj (xj) – UAj (xj) > 0 having subjectively treated all UBj (xj) – UAj (xj) < 0 as UBj (xj) – UAj (xj) = 0, where xj (j = 1, …, M) is the objective value of each option on dimension j (for an axiomatic analysis, see S. Li, Reference Li2001b). In other words, the decision maker’s task is to achieve a so-called “equated dominance,” that is, option A (B) dominates option B (A), having treated the smaller dimensional difference that option B (A) is better than option A (B) as subjectively equal. Hogarth (Reference Hogarth1987) and Payne (Reference Payne1976) stated that the dimension-based processes can be psychologically simpler to use and implement than the alternative-based processes. Using such a simpler process requires a dimension-based information search pattern, selective use of information about the options, and simple and ordinal comparisons (Su et al., Reference Su, Rao, Sun, Du, Li and Li2013; Zhou et al., Reference Zhou, Zhang, Wang, Rao, Wang, Li, Li and Liang2016).
Experiment 4 was designed to test whether the adults’ choices could be explained as being guided by a generalization of dominance detection; in particular, in a manner suggested by the equate-to-differentiate model.
Method
Participants
The poster advertising the experiment was posted in the online bulletin board system (BBS) of the Central University of Finance and Economics in Beijing. A total of 148 Chinese students (age range = 17–25 years; 89 females) on the campus of this university were approached to participate and were paid 10 yuan for their participation. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
Materials and procedure
The same three choice problems of the lantern and the mobile phone number scenarios in Experiment 2 were again used and tested. In light of a fictional representation system (with a monetary attribute and a non-monetary attribute) for describing each of the three choice problems, A is viewed as better than B on the monetary dimension, whereas B is viewed as better than A on the non-monetary attribute dimension (Figure 3). Participants were first asked to indicate \which option they would prefer to have on a 6-point scale (1 = strongly prefer A; 2 = prefer A; 3 = slightly prefer A; 4 = slightly prefer B; 5 = prefer B; 6 = strongly prefer B).
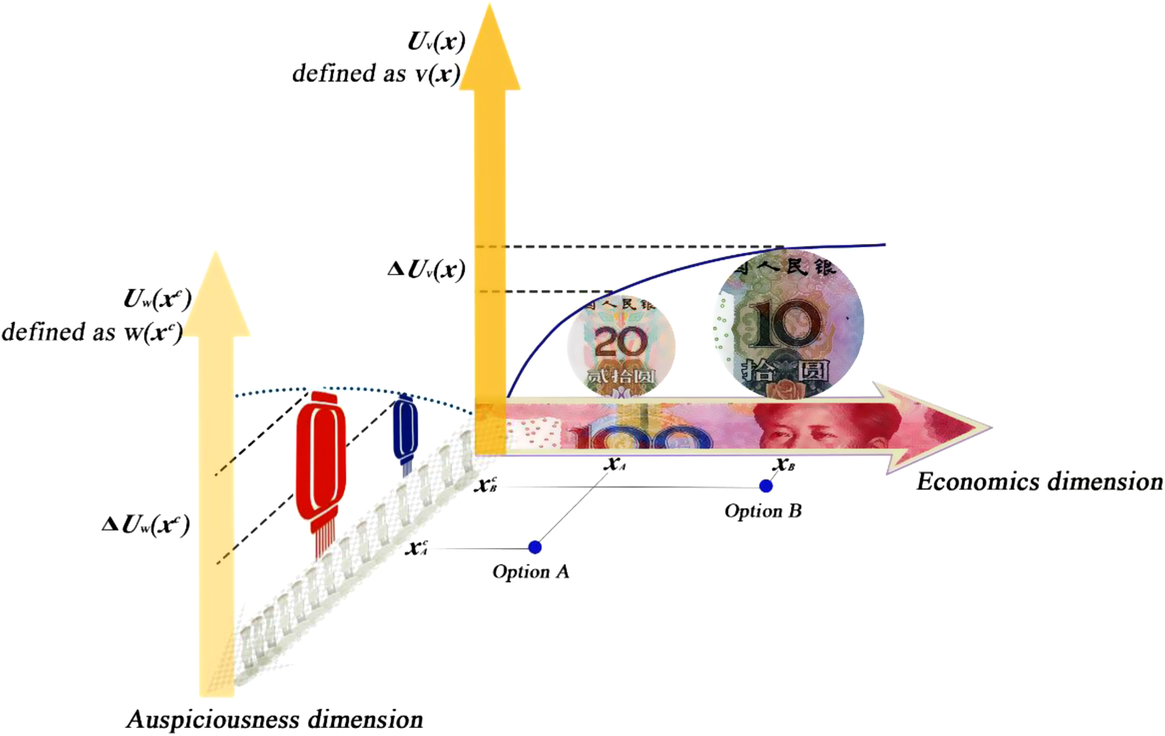
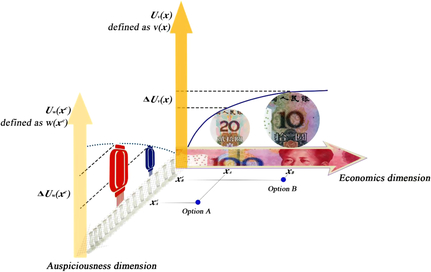
Figure 3. Choice between Option A (expensive lantern) and Option B (cheap lantern) represented as points in a multidimensional space, in which each dimension represents a distinct attribute that describes the object. The given (offered) dimension that presents the two options is the economics (monetary) dimension x, in which an expensive lantern (Option A) is presented as xA and a cheap lantern (Option B) as xB. The utilities (U v) assigned by the participants to x A and x B on the economics (monetary) dimension are defined as value (v[x]), v(x A) and v(x B), respectively. An additional unoffered/self-generated dimension that presents the two options could be the auspiciousness (non-monetary) dimension xc. Option A (an expensive lantern) and Option B (a cheap lantern) can be presented as x Ac (with luck) and x Bc (without luck), respectively. The utilities (U w) assigned by participants to x Ac and x Bc on the auspiciousness (non-monetary) dimension are defined as worth (w[xc]), w(x Ac) and w(x Bc), respectively. Given these two dimensions, the choice is considered a competition between ΔU v(x) established on a given dimension and ΔU w(xc) established on a generated dimension. The winner of the competition determines whether the final choice is simply one of choosing between the utilities established on a given monetary dimension or between those established on a generated non-monetary dimension.
Coupled with the three choice problems, a so-called “matching task”Footnote 4 was designed. The matching task offered a choice between two alternatives (labeled C and D) for which the option outcomes on each dimension were paired. The matching task was then given to one-third of the participants (see Table 5). These participants were asked in the matching task the alternative (e.g. C: “phone number ending with 513” vs. “phone number ending with 518” or D: “costs 10 yuan” vs. “costs 20 yuan”) that was the most different for them; that is, to determine which difference, Δ Uv(x) or Δ Uw(xc) in Figure 3, was subjectively greater.
Table 5. Contingency table for the choice and matching decisions in the colored lantern and the mobile phone number scenarios

Notes: CN1 indicates the alternative of “phone number ending with 513” vs. “phone number ending with 517”; CN2 indicates the alternative of “phone number ending with 513” vs. “phone number ending with 518”; CN3 indicates the alternative of “phone number ending with 514” vs. “phone number ending with 517”; CL1 indicates the alternative of “blue lantern” vs. “purple lantern”; CL2 indicates the alternative of “blue lantern” vs. “red lantern”; CL3 indicates the alternative of “white lantern” vs. “purple lantern”; D indicates the alternative of “costs 10 yuan” vs. “costs 20 yuan”. r indicates the point-biserial correlation (ps < .01). The data in bold type are those that were consistent with the equate-to-differentiate model.
Results and discussion
The results from the choice and matching tasks are summarized in Table 5. According to the equate-to-differentiate model, as soon as the dimension on which the utility difference is the greatest is determined, the decision maker’s objective is reduced to the choice of a better outcome along this dimension. That is, if C (D) is circled as being the most different, then B (A) will be chosen, and vice versa.
The prediction was satisfactorily confirmed by a point-biserial correlation analysis (the point-biserial correlation coefficients of the matching results and the choice results ranged from .46 to .87, ps < .01). A contingency table was generated by converting the 6-point data into binomial data. Chi-squared tests for the six choices on the contingency table revealed that 29–78% of the choice variance was significantly accounted for by matching (ps < .001).
The results indicated that the winner of the contest determines whether the final choice is simply one of choosing between the utilities established on a given monetary dimension or between the utilities established on a generated non-monetary dimension. In saying “generated”, we mean that there will be no dimensional difference at all (e.g. no value difference between “phone number ending with 513” and “phone number ending with 518”) if a new non-monetary dimension that signifies a distinct attribute that describes the options is not generated. These findings are of interest because they suggest that VM-violating (majority responses) as well as VM-satisfying (minority responses) choices are systematic, consistent, and predictable.
Experiment 5. Will adults shift back toward a choice that results in a VM decision if the difference between the utilities established on a generated dimension is reduced?
The results of Experiment 4 suggest that for the majority of adults, the greater one-dimensional difference between options is not the one established on the given monetary dimension but that established on the generated non-monetary dimension. In addition, the perceived greater difference between the utilities established on the generated non-monetary dimension prompts adults to choose the option with less monetary value. This finding raises the question: Can the final choice shift if the greater one-dimensional difference is changed from the generated non-monetary dimension to the given monetary dimension? Considering that our study of choosing the smaller pear will make sense only if the relationship between the offered monetary values remains unchanged, will adults choose the option with the greater monetary value if the difference between the utilities established on a generated nonmonetary dimension is reduced?
We sought the answer to this question in Experiment 5. We reasoned that the non-monetary dimensional difference between the options – for example, August 18 (a lucky number) versus September 5 (a non-lucky number) must be smaller when it is associated with a friend’s dinner party without being particular about where or when than it would be with a wedding banquet (Block & Kramer, Reference Block and Kramer2009) of meaning and image, which could induce a choice shift.
Method
Participants
Ninety-two adults (age range = 19–34 years; 59 females) working in manufacturing, retail, or service jobs participated voluntarily in the study through advertisements posted on bulletin boards at a supermarket in Jinan City. All of our participants were Chinese. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
Materials and procedure
A “wedding banquet” scenario and a “friend’s dinner party” scenario were constructed to manipulate the proposed non-monetary differences between options by applying lucky number 8 to a wedding banquet and a friend’s dinner party situation. Each scenario (which differed only in the text in brackets) contained a choice between a relatively economical or cheap banquet (Ұ3,000) and a relatively expensive one (Ұ4,000). The scenario reads as follows.
Wedding banquet/Friend’s dinner party scenario: Suppose you were to book a wedding banquet (friend’s dinner party). Faced with only two options, which would you prefer?
A. The banquet dated August 18 at the price of Ұ4,000
B. The banquet dated September 5 at the price of Ұ3,000
Each participant was asked to indicate the option they preferred and in which situation (wedding banquet or friend’s dinner party) they would take the date difference into account.
Post hoc investigation
To provide more direct evidence that the difference between the utilities established on a generated non-monetary dimension of the two options would be reduced from the wedding banquet scenario to the friend’s dinner party scenario, we asked another group of participants (N = 33, 23 females, age range = 18–23 years) to imagine themselves as restaurant managers and to set separate prices for the wedding banquet and friend’s dinner party on August 18 and in September 5. The results (see Figure 4) revealed that the mean price set for the wedding scenario (M = 1,137.89) was higher than that for the friend’s dinner party scenario, (M = 450.70), F(1, 32) = 9.60, p < .01, and that the mean price set on August 18 (M = 927.70) was higher than that on September 5 (M = 660.89), F(1, 32) = 5.93, p = .02. An interaction between date and scenario was also found, F(1, 32) = 4.32, p = .046. Further analysis revealed that the price on the lucky date was higher than that on the unlucky date for the wedding scenario (p = .03), whereas no significant difference between the lucky and unlucky dates was found for the friend’s dinner party scenario (p = .16). The pricing difference observed between the wedding banquet scenario and the friend’s dinner party scenario indicated that the difference between the utilities established on a generated non-monetary dimension was indeed reduced in the friend’s dinner party scenario.
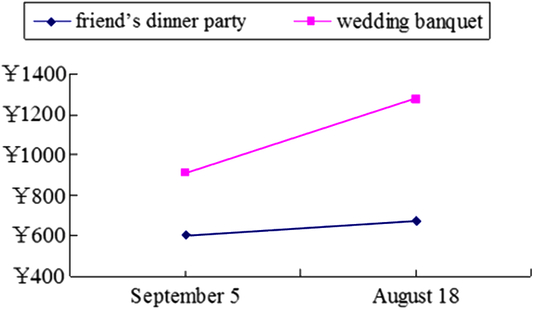
Figure 4. Mean price set by 33 participants for the wedding banquet/friend’s dinner party on August 18 or September 5.
Results and discussion
Similar to the findings in the mobile phone (with number 8) scenarios, the majority of the participants in the wedding banquet scenario also selected the option with the higher price (73.9% choosing the more expensive banquet date). Interestingly, for the friend’s dinner party scenario, the majority of the participants selected the option with the lower price (88.0% choosing the less expensive banquet date; see Table 6). Additionally, the majority (80.4%) of the participants indicated that the date difference should be considered for a wedding banquet but not for a friend’s dinner party.
Table 6. Percentage distribution of preferred option (higher price or lower price) as a function of type of banquet (wedding or friend’s dinner party)

Note: McNemar’s test, p < .001.
Overall, the results of Experiment 5 indicate that the principle of VM is obeyed in a friend’s dinner party scenario but violated in a wedding banquet scenario even when the offered parameters (the date and price) are identical in the two scenarios. This finding supports our proposition that adults will shift toward choosing between the utilities established on the given monetary dimension of offered options (i.e. selecting the option with the greater monetary value) when the difference between the utilities established on the generated non-monetary dimension is reduced.
Experiment 6. Were junior people (c.f. children) more willing to make value-based choices than senior people (c.f. adults)?
When a decision outcome is a smaller pear or an apparent loss, the most commonly used “self-defence” in daily life is likely to be “it’s worth the money”. In Experiment 3, when the more expensive option was chosen, frequently reported reasons included the term “worth”, implicitly suggesting something that is greater than monetary value. Specifically, social reinforcement (Skinner, Reference Skinner1958, Reference Skinner1971), future or delayed rewards (Green, Fry, & Myerson, Reference Green, Fry and Myerson1994; Rao & Li, Reference Rao and Li2011), cooperative decisions (Chen & Li, Reference Chen and Li2005), mutual benefits at all levels of life (Trivers, Reference Trivers2004), superstition value (Ng, Chong, & Du, Reference Ng, Chong and Du2010), and many other factors are all very likely to be captured by “worth” as unspoken gains.
Experiment 3 showed that the aspects fictionally represented on the generated dimension(s) by the participants for subjects who chose the option with less value are related to factors that have been socialized into their culture. Considering that individuals are socialized with age, we expected that junior people were more willing to make value-based choices than senior people. Experiment 6 was designed to test this expectation.
Method
Participants
Fifty Chinese senior citizens (age range = 47–70 years; 21 females) from the Community University in Beijing for the Aged and 50 young Chinese college students (age range = 19–21 years; 33 females) from the Central University of Finance and Economics in Beijing were recruited through advertisements in local social media (BBS) to fill out a short questionnaire in exchange for a small gift. The study was approved by the Institutional Review Board of the Institute of Psychology, Chinese Academy of Sciences.
Materials and procedure
The 514–517 pair from the phone number scenario and the blue–red pair from the colored lantern scenario in previous experiments were used in the present experiment. In addition, another two choices in a non-superstition context were designed. The choices read as follows.
Career scenario: Suppose you were a state-sponsored student studying abroad. Faced with a career decision, which would you prefer?
A. Working abroad with a yearly salary of $50,000 (approximately Ұ300,000)
B. Working in your home country with a yearly salary of Ұ200,000
Gift money scenario: Suppose you were given Ұ600 as a gift from your colleague when you got married; now is your colleague’s turn to get married. Which would you prefer to give your colleague?
A.Ұ600 as a gift
B. Ұ800 as a gift
Participants were first asked to indicate which option they would prefer to have with a 6-point scale (1 = strongly prefer A; 2 = prefer A; 3 = slightly prefer A; 4 = slightly prefer B; 5 = prefer B; 6 = strongly prefer B). They were then asked to make a value judgment and a worth judgment on a 7-point scale (for the value judgment, 1 = strongly agree that A produces more monetary losses than B; 7 = strongly agree that B produces more monetary losses than A; for the worth judgment, 1 = strongly agree that A is worth more than B; 7 = strongly agree that B is worth more than A).
Results and discussion
Similar to the previous scenarios, the majority of the participants in the newly added scenarios selected the option with the lower monetary value (68% chose the lower paying job; 62% chose to give more gift money), indicating a generalized violation of the principle of VM.
Experiment 6 was accomplished with regression analyses across the four scenarios, with the strength of preference as the dependent variable and the value and worth judgments entered simultaneously as independent variables (see Table 7).
Table 7. Regression analyses conducted with both younger and senior samples across the four scenarios
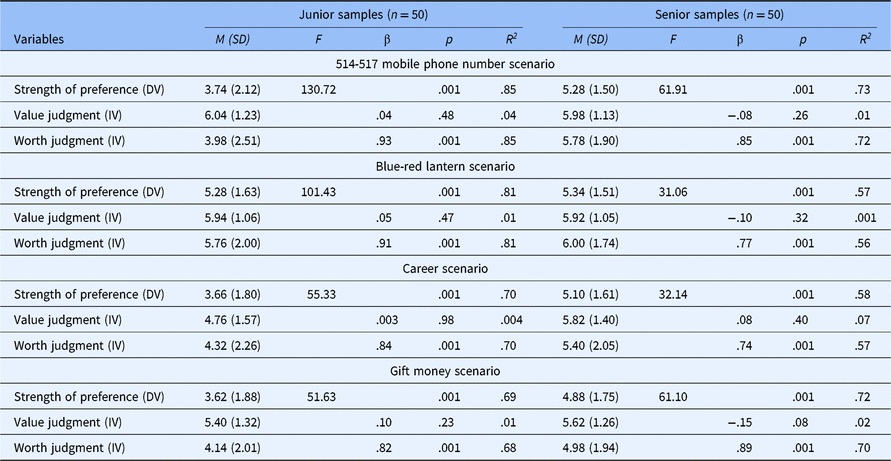
The results demonstrate that knowledge of the value difference between options does not permit the prediction of option selection (value judgment was a non-significant predictor, ps >.08) but knowledge of the worth difference between the options does (worth judgment predicted 56–85% of the variation in choice, ps <.001). That is, the chosen option could be viewed as having greater value or lesser value, but it is always perceived as having greater worth. As expected, the most preferred option across scenarios was also the most expensive or least valuable (M seniors + juniors = 4.52, SD = 1.14), and the preference for the option that generated greater worth was stronger for the seniors (M = 5.39, SD = 1.24) than for the younger respondents (M = 4.60, SD = 1.25), F(1, 99) = 10.21, p < .01.
The finding that the elders were less willing to make value-based choices, together with the finding in Experiment 2 that those who obeyed the principle of VM were not the parents but their children, generally supports our conjecture regarding the age effect on the choice of the “smaller pear” in our culture. As people grow older, they are socialized further into their culture, they learn other values of their culture, and therefore they easily generate a fictional dimension. Their ability to make a worth-based choice is then considered on the basis of individuals’ adaptive and survival strategies when they are socialized into their cultures.
General Discussion
Even at an early age, humans are clever enough to differentiate value of the offered options and make a value-maximizing choice. A child’s scientific ability is sometimes amazingly accurate (Cook, Goodman, & Schulz, Reference Cook, Goodman and Schulz2011). As people grow older and become more knowledgeable and socialized, they can foresee more possibilities in cause and effect relationships. They may then modify the rule of when to stop the decision process and, as suggested by this study, further explore the potential gains that are linked to the option but not explicitly expressed by a dimension offered by proposer. To achieve this goal, decision makers may creatively generate a new dimension and assign a delayed subjective value to the newly generated dimension, such as worth. When a decision is strictly based on the given set of dimensions, the equate-to-differentiate model suggests that our decision could be a simple choice between the values of options represented on one offered dimension or another (S. Li, Reference Li1994, Reference Li1995, Reference Li1996, Reference Li2001a, Reference Li2004, Reference Li2016). However, when a new dimension is generated, much of our decision making is a simple choice between the values assigned to the options on the given dimension or between the worth assigned to the options on the extra fictional dimension.
To test our choice model, we explored two forms of extreme worth (i.e. a very realistic resource and a very unrealistic superstition) that could give an offered “smaller pear” an even greater worth afterwards. In the superstition case, the supposed worth was attached to the consequences of the lucky number or color in the phone number (banquet) and colored lantern scenarios respectively. The role of these superstitious beliefs is similar to that of the “name letter effect” (Chandler, Griffin, & Sorensen, Reference Chandler, Griffin and Sorensen2008; Nelson & Simmons, Reference Nelson and Simmons2007; Nuttin, Reference Nuttin1987).
In the resource case, the supposed worth is something that pays back. This worth is assumed to be generated by a reliable resource, such as the experimenter or friend in the red packet containing money as gift/chocolate/pencil choosing problems or the home country or a colleague in the job-seeking and gift-giving scenarios respectively. These choice problems and those in the phone number (banquet) and colored lantern scenarios suggest that worth, although in very general terms (e.g., in little Kong Rong’s case), is applied only to a potential future reward that is fictionally represented on a generated dimension.
It is particularly noteworthy that, according to Yuval Noah Harari’s viewpoint presented in Sapiens: A Brief History of Humankind, “the ability to compose fictions”, namely, the ability to transmit information regarding things that do not exist at all (Harari, Reference Harari2014, p. 18), was notably the key for human beings to cooperate effectively in large numbers and to move up the food chain. The human superpower is really based on fiction (see Bloom, Reference Bloom2017). The worth-based choice, which was proposed in the present study, could then actually be seen as a process of “fiction-generating”. Without an ability to imagine things that do not actually exist, decision makers were unable to generate an unoffered dimension, nor could they assign a delayed utility (worth) to the options on the self-generated dimension. By considering the fiction perspective, the concept of worthFootnote 5 that we introduced in this study should be stressed as considered a future or delayed utility. Using as an example the Chinese idiom, “A book holds a house of gold” (书中自有黄金屋), the later reward of a house of gold requires time to attain collective understanding and individual realization. The central idea, as proposed by Harari (Reference Harari2014, p. 149), is that money is not a material reality – it is a psychological construct. Dollars have value only in our common imagination.
Although the concept of fiction-generating ability has been proposed by Harari (Reference Harari2014), the lack of an operational definition prevents genuine understanding. Therefore, we are optimistic that the ability to further generate a fictional dimension, to assign a delayed utility (worth) to the options on the fictional dimension, and to make a worth-based choice as described in the present study, could eventually be deemed the operational definition to measure the degree of “fiction-generating ability” developed by Harari (Reference Harari2014).
It would be relevant to notice that the fictional issue under investigation is not isolated. An increasing number of researches could be brought or placed under the umbrella of “choosing option with less value (i.e. giving away the bigger pear)”. Hu et al. (Reference Hu, Li, Jia and Xie2016) sought to address the question of whether the potential future reward received by an altruistic performer could be any positive internal reward. In the language of our model, the so-called positive internal reward could be effectively represented on an unoffered but fictional dimension. Recently, O’Brien and Kassirer (Reference O’Brien and Kassirer2018) determined that the joy of giving lasts longer than the joy of getting. They found that the happiness we get from giving appears to sustain itself. In the language of our model, the so-called “happiness we get from giving” may be rephrased as follows: act of giving (c.f. giving away pear) is represented on an offered (monetary) dimension; moreover, no utility, such as happiness, will be assigned to the “act of giving” on the monetary dimension unless the donator will self-generate an extra fictional dimension (e.g. social reinforcement) to present the. act of giving.Footnote 6
More relevantly, in Tang et al.’s (Reference Tang, Zhou, Zhao and Li2014) study, four factors/dimensions, that is, 惠 (favor), 善 (virtuous), 义 (righteousness), and 法 (law), which underlay worth-based choice were extracted using exploratory factor analysis, and the four-factor construct proved to be reliable and valid based on the results of confirmatory factor analysis. Zhao et al. (Reference Zhao, Shen, Rao, Zheng, Liu and Li2018) reported that people with a higher tendency to accept an option resulting in loss (e.g. unpaid overtime, counterfeit cash, or signing away an inheritance) were more likely to report higher scores on subjective well-being and the Socioeconomic Index, which is further enhanced with increasing time interval. The revealed material or mental benefits in Zhao et al.’s (Reference Zhao, Shen, Rao, Zheng, Liu and Li2018) survey are important and support our conjecture that an extra dimension exists that is not offered but is self-generated. This is because the real but later benefits (either material or mental) can be analogously seen as that little Kong Rong’s later successes can be fictionally represented on an extra unoffered/self-generated dimension (c.f., social reinforcement).
The idea of the generated dimension is also taken literally in neuroeconomics. In a review paper on the common neural currency for social and monetary rewards, Saxe and Haushofer (Reference Saxe and Haushofer2008) suggest that some rewards in life are more valuable than money. However, to state that love is worth more than money is to imply a third scale: a common “currency” in which physical and social rewards can be measured and thus compared. In a recent functional magnetic resonance imaging (fMRI) study on the neural basis of superstition, Rao, Zheng, Zhou, and Li (Reference Rao, Zheng, Zhou and Li2014) found that the middle/superior frontal gyrus showed a significantly stronger neuronal deactivation for the auspiciousness-based choices than for the economics-based choices and that the activation of the right middle/superior frontal gyrus in the auspiciousness-based versus economics-based choice contrast was significantly correlated with individuals’ wedding date-related superstitious beliefs. These findings suggest that a specific brain region is responsible for superstitious beliefs (i.e. a type of “worth” established on an extra dimension).
Our findings suggest that children have difficulty choosing options with less value because they are unable to generate an extra dimension and assign worth for the offered options. In contrast, for older people, the chosen option is always the option with the greater worth, regardless of whether it is of greater value. Such a finding is in agreement with the dynamics of knowledge accumulation: forming a fictional entity of cultural heritage requires time, and trusting in such a fictional entity (e.g. wedding date or gift) requires time as well. As time progresses, the imagined reality becomes increasingly powerful (Harari, Reference Harari2014).
Further analysis of a worth-based choice indicates that the development of the contingency between the potential reward and the worth-maximizing choice is unstable and slow. Not everyone is born with the ability to imagine an option with low value as the “ugly duckling”. In contrast to the strategy of value-based choices that is developed early in life, the strategy of worth-based choices is developed later in life. The age effect on individual life spans that was detected in our study supports this conjecture. Further supportive evidence may be generated from the evolutionary history of human society from hunting to farming. This evolution is possible only if humans are brave enough to make the risky decision of losing edible seeds now and yielding derived products seasons later. Other evidence that highlights the difficulty of making worth-based choices can be found in our legal system. Considering that what should be protected by law is morally correct yet vulnerable, an unstable and slowly formed choice behavior that requires extra attention and protection makes sense. Our legal system and society tend to value and treat value- and worth-based choices differently. An act of immediate gain and later nothing or even a larger loss (e.g., drug abuse or a usurious loan) is punished by law, whereas an act of immediate loss and a later larger gain (e.g. education investment or charity donation) is generally protected.
To summarize, this study investigated choices in which the options’ values were established on a fixed set of dimensions that were not value-maximized in a framework of worth-based choice. It clarifies the mechanisms of making a loss choice and provides an improved understanding of why people do not choose the option with the apparent greater value. An important implication of this study is as follows. In real life, numerous people remain uneasy and willing to move “one step further” than ordinary people. In this study, the so-called “one step further” is to generate an additional dimension more than others, to assign an additional utility to the offered options, and then make a worth-based choice. If you say, “We are what we choose” (Bezos, Reference Bezos2010), such a “one step further” choice may serve as a behavioral marker to distinguish qualified from unqualified Homo sapiens (Shen, Chen, Guo, & Li, Reference Shen, Chen, Guo and Li2018) or even serve to solidify human beings’ top position in the food chain.
As further research is pursued, two issues are worthy of special consideration. First, the extent to which the present findings may apply to other countries’ contexts must be determined. Given that our research was conducted “with Chinese characteristics” in terms of samples, scenarios and other aspects, cross-validating our findings from one country to another would be worthwhile. From a collective view that fiction has enabled us not merely to imagine things, but to do so collectively, the concern is reasonable. Various fictional dimensions of “Chinese characteristics” have been generated by our Chinese samples; such fictional entities as the lucky numbers and others would work if and only if we all believe in the same fictional stories or common myths (Harari, Reference Harari2014). Second, the extent to which we can improve our approach to identify the additional fictional dimension and measuring dimensional differences between offered and generated dimensions must be ascertained. In this study, the additional fictional dimension between options was chiefly identified by utilizing query theory. Using some neuroscience measures, such as fMRI, is a promising approach to explore whether a neural basis for such a fictional dimension exists (e.g. Rao et al. Reference Rao, Zheng, Zhou and Li2014).
Author ORCIDs
Shu Li 0000-0003-4402-1674
Acknowledgments
This research was partially supported by the National Natural Science Foundation of China (No. 71761167001; 31471005; 71701114), the Major Project of National Social Science Foundation of China (18ZDA332; 17ZDA325), Key Projects of National Social Science Foundation of China (16AZD058) and Humanity and Social Science Youth Foundation of Ministry of Education of China (14YJC630208). The authors thank Libo Li from School of Mathematics and Statistics, University of New South Wales for his assistance with concept expression, Yi-Ping Tang for his assistance with data collection, Guang-Hui Shen for his help in preparing experimental materials, Shu-Wen Yang for her writing or editing assistance, and Xiao-Ming Wang for her assistance with graph work.
Financial Support
None.