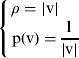1. INTRODUCTION
Localization is a key capability of autonomous navigation of vehicles and robots. The Global Positioning System (GPS) has been the most widespread navigational system used in outdoor navigation. However, navigation methods relying on GPS can be vulnerable, and the signals may be disturbed in urban environments with tall buildings or elevated rails. Worse, it is not available in specific areas such as underground locations and outer space. However, integrated vision navigation is a technique that uses single or multiple cameras to acquire 2D image information from a scene, and then performs the navigation by applying algorithms such as image processing, computer vision, and object recognition to locate the 3D dynamic positions. In the non-GPS environment, integrated vision navigation is more advanced than other techniques. It is a passive positioning technique with good imperceptibility, high observation speed, and good accuracy. On the other hand, integrated vision navigation can avoid some strict environmental restrictions because it does not depend on any signal or radiant sources. However, it still becomes a problem when real-time and high-precision performance is required.
DeSouza and Kak (Reference DeSouza and Kak2002) presented an investigation of the developments in the fields related to vision for mobile robot navigation in the past 20 years. The differences in how vision is used for indoor and outdoor robots are large; thus they divided their investigation into two different categories: indoor navigation and outdoor navigation. Indoor navigation was then focused on map-based, map-building-based and mapless navigation. The map-based navigation solution is supported by providing the robot with a model of the environment. It is proposed by providing automated or semi-automated robots that could explore their environment and build an internal representation. However, the mapless navigation solution relies on the integrated navigation system without considering any prior description of the environment. Compared with indoor navigation, outdoor navigation usually involves obstacle-avoidance, landmark detection, map building/updating, and position estimation. Thus, outdoor navigation is concentrated on structured and unstructured environments, and some progress can be efficiently made to represent the uncertainties in a robot's knowledge of its environment as well as its own relative position in the environment.
A first prototype of the vision navigation system ‘NavLAB’ was developed by Carnegie Mellon University (Thorpe et al., Reference Thorpe, Hebert, Kanade and Shafer1988). It mainly considered path tracking and 3D vision. The area correlation-based method is used in path tracking by dividing an image into road and non-road points. This method can adaptively select road models according to different roads and environments, and the most likely road border point is determined based on the acquired road or non-road points to finally achieve path recognition and tracking. After 3D information has been acquired via point-cloud processing from ERIM LIDAR data, 3D vision is performed to optimize the vehicle navigation by recognizing track obstacles and analysing track terrains.
The Chinese Academy of Sciences (Su and Zhu, Reference Su and Zhu2005) presents a design method for a novel configured stereo vision navigation system for mobile robots, which is a catadioptric sensor called the Omnidirectional Stereo Vision Optical Device (OSVOD), based on a common perspective camera coupled with two hyperbolic mirrors. As the hyperbolic mirrors ensure a Single View Point (SVP), the incident light rays are easily found from the points of the image. The two hyperbolic mirrors in OSVOD share one focus that coincides with the camera centre, which is coaxially and separately aligned. Thus, the geometry of OSVOD naturally ensures matched epipolar lines in the two images of the scene. The separation between the two mirrors provides a large baseline and eventually leads to a precise result. The properties mentioned above make OSVOD especially suitable for omnidirectional stereo vision because depth estimation depends on speed, efficiency and precision. The proposed system can be used by mobile robots for obstacle detection, automatic mapping of environments, and machine vision where fast and real-time calculations are needed.
Actually, the application of Visual Odometry (VO) and IMUs on Mars exploration rovers are famous and successful examples; they enabled the rovers to drive safely and more effectively in highly-sloped and sandy terrains. After moving a small amount on a slippery surface, the rovers were often commanded to use camera-based VO to correct its errors in the initial wheel odometry-based estimation when the wheels lost traction on large rocks and steep slopes (Cheng et al., Reference Cheng, Maimone and Matthies2005; Maimone et al., Reference Maimone, Cheng and Matthies2007).
Another successful application of VO/IMU integration is in the natural environment revealed by Konolige et al., (Reference Konolige, Agrawal and Solà2007). In this algorithm, an Extended Kalman Filter (EKF) was used for VO and IMU data fusion via loose coupling. It is implemented for three steps:
• Step 1. The EKF formulation starts with motion prediction from VO.
• Step 2. The IMU is used as an inclinometer (absolute roll and pitch) to correct the absolute gravity normal.
• Step 3. The IMU is used as an angular rate sensor (for incremental yaw) to correct relative yaw increments.
By using these techniques, the EKF attains precise localization in rough outdoor terrain. As the author presented, a typical result is less than 0·1% maximum error over a 9 km trajectory, the IMU used in the system with Gyro bias stability of 1 deg/h.
Later, Bayoud developed a mapping system using vision-aided inertial navigation (Bayoud and Skaloud, Reference Bayoud and Skaloud2008). The system employs the method of Simultaneous Localization and Mapping (SLAM) where the only external inputs available to the system at the beginning of the mapping mission are a number of features with known coordinates.
Stereo image-matching is one of the key techniques in integrated vision navigation. It is a process of calculating selected features and building relationships between features to match the image points in different images. Image matching is a process that identifies the relationship between a reference image and the image under investigation. A great number of image-matching algorithms have been proposed in recent decades. These algorithms are classified into two categories: pixel-based and feature-based. Pixel-based algorithms can robustly estimate simple transition motion but may fail when dealing with either images with serious transformation or highly degraded images. Optical flow and pixel correlation are two of the most popular pixel-based methods (Lucas and Kanade, Reference Lucas and Kanade1981; Castro and Morandi, Reference Castro and Morandi1987). Feature-based algorithms have recently been widely developed (Mikolajczyk and Schmid, Reference Mikolajczyk and Schmid2005). They can offer a robust image-matching capability when tackling dramatically changed or degraded images, which are invariant to image transition, scaling, rotation, illumination, and limited ranges of viewpoint changes. Feature-based algorithms can have higher image-matching performance than pixel-based algorithms in terms of reliability and precision.
However, feature-based algorithms are not practical for some real-time applications because of the nature of computational complexity and the huge memory consumption. For a feature-based method, Bay et al., (Reference Bay, Tuytelaars and Van Gool2006) proposed the Speeded Up Robust Feature (SURF) algorithm based on previous research results by considering the time assumption. SURF uses the integral image to approximate the Gaussian convolution, thereby accelerating the convolution process. However, SURF still displays a weakness in matching robustness and results in addition to wrong matching points. Moreover, it is still considered too slow to be adopted for real-time applications even though it has significantly improved the processing speed of feature extraction and generation of the feature descriptors.
Song (Reference Song2004) then analysed the basic theory of binocular stereo vision and studied the key technique of linear feature stereo matching, which is the strategy of camera calibration, feature abstraction, and matching strategy. He first proposed an improved two-step camera calibration method, which obtains interior and exterior orientation elements and lens distortion parameters. At the same time, the proposed method removes control points with large errors and iterations to retrieve more accurate parameters. Song extracted a continuous single-pixel width segment using phase grouping and a heuristic connecting segment extraction algorithm. Finally, he proposed a novel stereo-matching strategy based on the geometry features and corner points of neighbouring segment regions. The matching and calibration results are both optimized with epipolar and parallax continuity constraints.
Results show that although stereo-matching has been developed for years with great achievement, several theoretical and technical problems remain to be addressed. For example, the method based on feature matching produces great computation but is hard to use in high real-time demand applications. The problem of executing a fast match of common points between images is the core issue of stereo-matching. Another challenge in stereo-matching is the ambiguity of the matching results. Under certain circumstances, two independent images share many similar features or pixels, resulting in the resolution of big barriers. The results of stereo-matching can facilitate the fast measurement of the 3D coordinates of an object; however, a challenge is presented when the image is acquired at high speed, such as in a moving vehicle. Thus, a new vision navigation system based on image matching and photogrammetric theory is proposed in the current paper, and the determination of real-time, 3D positions from the sequence-based image is also discussed.
2. STEREO CAMERA CALIBRATIONS
One of the most important tasks of computer vision is to reconstruct a 3D model of the real world and recognize objects by implicitly analysing geometric information included in the images captured by a camera. The spatial geometric information of a point and its corresponding point in the image space is determined by the model parameters of the camera, and in most conditions, these parameters are not easy to know directly. However, they can still be obtained via experiments, known as camera calibration. Camera calibration determines the geometric and optical parameters of the camera, and the orientation and position parameters of the camera coordinate system relative to the object coordinate. This process greatly affects the accuracy of computer vision.
Furthermore, camera calibration determines camera position and property parameters, and establishes the imaging model, which determines the show points in the space coordinate project and their correspondence in the image plane. An ideal optical projection imaging model is the central projection, also known as the pinhole model. The pinhole model assumes that the reflected light is projected onto the image plane, which satisfies the conditions for direct light transmission. The pinhole projection model consists of the centre of the projection, the image plane, and the optical axis (Figure 1).

Figure 1. Pinhole projection model.
Most existing camera models are parametric and currently use the following camera calibration methods (Pei, Reference Pei2010):
• Direct linear transformation method: fewer parameters involved, convenient to compute.
• Perspective transformation matrix method: builds the camera's imaging model through the perspective transformation matrix.
• Two-step camera calibration: initially uses the perspective transformation matrix method to solve the linear camera parameters, and then uses these parameters as initial values, considering the distortion factors to obtain nonlinear solutions using the optimization method.
• Two-plane calibration method.
The camera calibration module of the commercial software iWitness® used in the current experiment can easily access the internal and external parameters of the camera. Figure 2 shows the calibration results using the actual image shooting in Tongji University, Shanghai, China and the corresponding coordinate data. From the experimental results, the camera centre and focal length measured by a non-measurement camera exhibits significant deviation from the actual values, resulting in greater deviation in the subsequent resection experiment. Therefore, the camera must be pre-calibrated before a non-measurement camera is used in the measurements; otherwise, the accuracy of the subsequent results would be reduced.

Figure 2. Camera calibration result.
3. SURF-BASED IMAGE-MATCHING ALGORITHM
The purpose of stereo image matching is to find the correspondence in two or more images of the same scene shot from different perspectives. For any kind of stereo-matching method, the effectiveness of the solution depends on three key areas, namely, choosing the right matching features, looking for their essential properties, and then establishing a stable feature-matching algorithm. In the present research, feature selection can be divided into two categories, namely, region-based image correlation matching (area-based matching), and features-based image correlation matching.
According to the selected feature, feature-based matching can be subdivided into point-matching, line-matching and surface-feature matching. In general, feature-matching can be done in three steps: (a) feature extraction, (b) feature description, and (c) feature matching. Compared with other matching algorithms, the feature-based matching algorithm does not directly depend on the characteristics of grey, and thus is significantly more robust. Meanwhile, these algorithms can be calculated faster and relatively easily deal with disparity discontinuity regions. However, their matching accuracy largely depends on the accuracy of matching point detection.
3.1. Principle of SURF-Based Image-Matching Algorithm
In 2006, Herbert Bay proposed a novel scale and rotation-invariant interest point detector and descriptor and named it ‘Speeded Up Robust Features’ (SURF). It approximates and even outperforms previously proposed schemes in the areas of repeatability, distinctiveness, and robustness, and can be computed and compared much faster (Bay, Reference Bay, Tuytelaars and Van Gool2006). This performance is achieved by relying on integral images for image convolutions; by building on the strengths of the leading existing detectors and descriptors (specifically the Hessian matrix-based measure for the detector, and a distribution-based descriptor); and by further simplifying these methods.
3.1.1. SURF Algorithm
The SURF algorithm can be divided into three typical steps, namely, accurate interest point localization, interest point descriptor, and feature vector matching (Figure 3).

Figure 3. Flow chart of SURF.
3.1.2. Matching result of SURF
The program used in the current article is based on the function of the open-source library OPENCV. Figure 4(a) shows the matching result of a standard Graffiti scene, Figure 4(b) shows the result of the surveying building in Tongji University, and Figure 4(c) shows an image of the Germany centre. The size of the three images are 800×640 pixels, and in each image there are over 200 feature points. These three matching results show remarkable accounts of error-matching points (label 1 is the correct matching point, whereas the labels 2 and 3 are error-matching points). Further improvement is necessary to use these matching results for future measurements.

Figure 4. SURF-matching results.
3.2. Improved SURF-Based Image-Matching Algorithm
SURF significantly improves the matching efficiency. However, it also reduces the matching stability and results in increased error-matching points. Certain measures must be taken to reduce the number of error-matching points because they are highly important in the follow-up application.
3.2.1. Improvement Strategy
Given that most points have achieved correct matching in the original SURF matching process and only a small number obtained error matching, the original matching results are treated as coarse results with gross errors. In addition, because the same 2D point coordinates in both images have been obtained during the original matching process, the improvement takes the translation, rotation, and scaling parameters between these two images into account using a robust parameter estimation method for estimation, and a certain threshold is set. The deviation between the original and estimated results is compared, and points with low accuracy are removed, thereby obtaining better matching results. The following equations show the translation model and the specific robust estimation function used in the current paper.
• Image translation model:
(1)Assign c=μ cos α, d=μ sin α (2)
(2)
• The ‘Selecting Weight Iteration’ method is used for a robust estimation. The specific method is called a “Norm minimization.” Its ρ and weight function are expressed as:
(3)
The flow chart of the improved SURF algorithm is shown in Figure 5.

Figure 5. Flow chart of the improved SURF algorithm.
3.2.2. Experimental Result of the Improved SURF Algorithm
The same images appearing in the SURF process are used in the current experiment. Figure 6(a) shows the improved result of the standard Graffiti scene and Figure 6(b) shows that of the surveying building. Figure 6(c) shows the Germany centre. The number of matching points in the figures decreases, but the matching accuracy obviously improved. Moreover, the improved SURF algorithm does not significantly increase the execution time (Table 1). Therefore, the improved algorithm appears effective.

Figure 6. Matching results of the improved SURF.
Table 1. Comparison between the efficiencies of the original and improved SURF.

4. THREE-DIMENSIONAL POSITIONING FROM AN IMAGE SEQUENCE
4.1. Rough Navigation and Position
In the image sequence, the intersection theory from photogrammetry can be adopted to calculate the corresponding positions of these feature points in the object space if the exterior parameters of the first and second image and the image coordinates of the same point are known. Another resection operation is performed to obtain the orientation and position parameters of the third image. The exterior parameters of the second and third images are already known; hence, the intersection and resection can be continuously operated until a Three Dimensional (3D) coordinate measurement is achieved. The entire process is shown in Figure 7. The specific calculation strategy is as follows:
• The exterior parameters of the first and second images are calculated using the image coordinates of the feature point and the corresponding 3D coordinates in object space (POS1 and POS2 in Figure 7).
• The matching points between the first and second image are identified, and the 3D coordinates of the point in the object space are obtained using the matching result (that is, the coordinates of points A, B, C, D, and E).
• The object coordinates obtained from the second step are passed to the third image using the matching result from the second and third images.
• The exterior parameters of the third image are calculated (obtaining the posture of POS3, as shown in Figure 7).
• The matching points in the second and third images are recalculated and their 3D coordinates in the object space are obtained using the intersection theory (i.e., the 3D coordinates of F, G, H, and J are retrieved).
• The same operations from the fourth image are executed until the task is completed.
After finishing the feature matching, the image point coordinates of feature points can be obtained in stereo images based on photogrammetry mathematic model. Here the titled bundle adjustment is used to get the exterior orientation parameters of cameras and the 3D coordinates of unknown ground points as well. Bundle adjustment is based on collinearity equation, making the bundles intersect optimally by means of rotating and transforming. For each matched feature point, two error equations can be formed.

Where, v x and v y are observation residuals of image point coordinates, a 11−a 16, a 21−a 26 are coefficients of error equations, dX s, dYs, dZs, dφ, dω, dκ are correction values of exterior orientation parameters, dX, dY, dZ are correction values of 3D coordinates of unknown ground point, for control points, dX, dY, dZ are zero, l x and l y are deviation of observation of image point coordinates and approximate values in the iteration process. For each matched point, an error equation could be established. After all the error equations are established, we would use the iterated solution to get correction values of exterior orientation parameters and 3D coordinates of unknown ground points based on Least-squares principle.

Figure 7. Image sequence-based coordinate measurement.
The data shown in Tables 2 to 4 are used in the current experiment. Tables 2 and 3 show the feature point image coordinates and their object coordinates in the first and second images, respectively, which are used to calculate the exterior parameters. Table 4 shows the calculation results, as shown in Figure 8.

Figure 8. Exterior parameters of the image sequence.
Table 2. Coordinates on the left image.

Table 3. Coordinates on the right image.

Table 4. Retrieved posture results.

4.2. Obtaining the Image Exterior Parameter Through IMU
The relative spatial position and attitude relation between the IMU and the camera must be calculated to facilitate the integration with IMU and achieve optimization (Figure 9). The calibration consists of two steps: (1) determining the offset between the camera projection centre and the geometry centre of the IMU; and (2) determining the rotation matrix between the image space coordinate system and the carrier coordinate system (original at the centre of the IMU).

Figure 9. Spatial relationship between IMU and the camera.
The calibration is performed in an experiment ground with sufficient number of feature points. firstly, two points, named A and B, are selected, with their coordinates obtained via differential GPS, then Gauss projection is performed to obtain their Gaussian coordinates, so they can be used as control points in the following total station survey. The procedure is as follows:
• n feature points on the ground are selected and marked as control points in the resection process, and their 3D coordinates are obtained via total station survey. Images are shot with the camera and their exterior parameters are retrieved according to the resection theory, so the transformation matrix R Ce from image space coordinate system to Earth-Centred Earth-Fixed (ECEF) coordinate system is obtained.
• The carrier vehicle is placed in a suitable position and angle and kept stationary. The IMU continuously obtains measurement data. For a high accuracy IMU, the attitude (pitch, roll, yaw) of the carrier vehicle can be obtained through initial alignment, however, for a low accuracy IMU, in which the gyro is not able to sense the earth's rotation, we can only obtain pitch and roll angle; thus, the yaw angle should be obtained by other means. For our carrier vehicle, the base is designed in the shape of rectangle, and the IMU is mounted aligned to its centre line. So the coordinates of the four corner points of the carrier base are measured, and the carrier heading angle is obtained.
While the IMU stays stationary, it outputs the gravitational acceleration g and the component of Earth's rotation angular velocity in the carrier coordinate system. However, an IMU with low accuracy cannot sense the Earth's rotation. Therefore, only the pitch and roll angle can be calculated from the IMU output.
The output gravitational acceleration while stationary is assumed as g b; that is:
The component of the gravitational acceleration g in the local coordinate is assumed as gL. This component can be easily retrieved as follows:
These assumptions satisfy the following equation:
where RLb is the rotation matrix between gb and gL.
In detail, the above equation can be expressed as:

Thus, the expression for the calculation of the pitch and roll angles is:

The azimuth of the carrier can be presented by the midpoints of the front and back ends. The midpoint of the front end is marked asC 0, and that of the back end as D 0. Thus, the following equation is obtained:

The following equation is used to retrieve the carrier azimuth a:
Hence, the attitude matrix of the carrier can be directly calculated using the p, r, and y values:

where y=2π−a.
When the R bL and R Ce values are known, the rotation matrix can be easily calculated:
where R eL is the rotation matrix from the ECEF to the local system, which depends on the latitude and longitude of the carrier.
R eL can be expressed as follows:

where:
φ is latitude.
λ is longitude.
φ and λ are obtained from the linear elements of camera's exterior parameters.
R Ce is the rotation matrix from image space coordinate system to ECEF.
R Ce can be expressed as follows:

where, ϕ, ω, κ are three Euler angles from image space coordinate system to ECEF, which are angle elements of the camera's exterior parameters.
The coordinates can be retrieved from the centre of the IMU, and its offset to the centre of the camera can be obtained.
4.3. Optimization with the Integrated IMU
As a key part of the algorithm, the integration of the VO and the IMU using an EKF will be implemented; actually, a wheel odometry is also used in our system which can provide velocity information of the carrier. Two approaches are considered: one is that, when the image features are sufficiently rich, we use the estimated position and attitude of the camera via bundle adjustment to calibrate the gyro drifts, accelerometer bias, scale factor error of the wheel odometry with EKF; the residuals of the camera position and attitude can also be estimated. Once all these sensor errors are calibrated, a high accuracy can be obtained and used to support the estimation of the parameters for situations in which the image features are too poor to determine the camera's position or attitude; this needs another approach to be considered. Under this situation, only IMU measurements and wheel odometry data are used for integration, and the estimated position and attitude are transformed and assigned to the camera.
VO and IMU are fused via loose coupling, in which each subsystem is taken as an independent estimator. In the current paper, an indirect Kalman filter is used to estimate the system errors. The error state considers the INS navigation parameter errors, IMU errors, and scale factor errors for the wheel odometry. The dynamic equation of the system is based on the INS error equation.
The error state vector can be written as
where δrL, δvL, δεL, d and b are 3D position errors, 3D velocity errors, 3D misalignment angles, 3D gyro drifts, and 3D accelerometer bias for the INS, respectively.
δk is the scale factor error of the wheel odometry.
The error state vector can also be written as
The system dynamic equation is described as follows:
![$$\mathop X\limits^\cdot = \left[\openup2 {\matrix{ {\mathop {F_{ins}} \limits_{15 \times 15}} & {\mathop O\limits_{15 \times 1}} \cr {\mathop O\limits_{1 \times 15}} & 0 \cr}} \right]\left[\openup2 {\matrix{ {X_{ins}} \cr {X_{od}} \cr}} \right] + G \cdot W$$](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151127083647536-0836:S0373463312000264_eqn18.gif?pub-status=live)
where F ins is the coefficient matrix of the INS error equation, which can be derived from the INS navigation equation in the local-level frame, and G is the process noise dynamic matrix.
The inputs to the Kalman filter include the velocities from the INS outputs and wheel odometry measurements, the coordinates from the INS outputs and VO outputs, and the attitude angles from the INS outputs and VO outputs. The measurement equation can be written as follows:

where:
Z v, Zr, Za are filter measurements.
H v, Hr, Ha are matrix measurements.
V v, Vr, Va are the residuals.
The velocity errors can be denoted as:
where V odb is the velocity of the vehicle in a forward direction as measured using the wheel odometry.
The measurement matrix for the velocity errors can be derived as follows:

The position errors can be denoted as:
where:
r ins represents the position of the vehicle obtained from IMU.
r image represents the position of the vehicle obtained from VO.
The position vector r image should be expressed using the origin in the IMU centre by subtracting the lever arm between IMU and the camera.
The measurement matrix for the position errors can be easily written as follows:

The attitude errors can be denoted as:
where:
a ins represents the attitude of the vehicle obtained from IMU.
a image represents the attitude of the vehicle obtained from VO.
The attitude vector a image should be denoted as the attitude that relates the body frame with the local-level frame, by taking into account the calibrated result of the transformation matrix between IMU and the camera.
The measurement matrix for the attitude errors can be used to determine the relationship between the attitude errors and the misalignment angles. The equation can thus be derived as follows:

In a filter circle, the state error is estimated and compensated in the system, and the parameters for VO are also adjusted
where ![]() is the output of the Kalman filter for the error state estimation, and
is the output of the Kalman filter for the error state estimation, and ![]() ,
, ![]() are the adjustment parameters for VO.
are the adjustment parameters for VO.
Figure 10 summarizes the Kalman filter frame for the visual odometry/IMU integration. The system is a closed loop Kalman filter, the outputs of which are fed back to the system. When the solution for VO succeeds, the calibrated parameters for VO after the filtration process return, and the estimated IMU errors and wheel odometry error are calibrated. Thus, the integrated system can maintain high accuracy for some time, even under the occasional short-lived VO solution failures. When the VO solution fails, the only inputs are the velocities from INS and the wheel odometry, with no VO inputs. Kalman filtering for the integrated IMU/wheel odometry system is implemented, and the outputs, which are the optimal estimated INS parameters (position and attitude), are passed on to the camera. In both cases, the coordinates of the matched feature points would be recalculated via a forward intersection using the estimated parameters for Kalman filtering for the camera.

Figure 10. Visual odometry/IMU integration Kalman filter.
5. EXPERIMENT AND RESULTS
The author developed a hardware system, including a stereo camera pair, an IMU, a wheel sensor, a computer, and a router, all mounted on a navigation vehicle, as well as a computational software based on the algorithms presented in the current paper. The IMU used in our system consists of three Fibre Optic Gyros and three MEMS Accelerometers. Gyro bias stability is 0·005 deg/s. Accelerometer bias stability is 10 mg. The type of stereo cameras is progressive scanning CCD, the baseline is 30 cm, the focal length is 12 mm, and the image frame is 696×520 pixels, with pixel size of 6·45μm×6·45μm, the field of view in horizontal and vertical are 42° and 31°. The system is capable of data collection and navigation solution in real time.
We conducted an experiment in a realistic situation to demonstrate the validity of our algorithm. The experiment is performed in an open square located in Beijing, see Figure 11. The entire process lasts for approximately 45 minutes, with the vehicle running at a distance of about 1150 m. The data set collected includes images, IMU data, wheel sensor data, and RTK GPS data. In the data collection process, the images are captured at a rate of 2 Hz, and the total images collected are over 4300 frames. The wheel sensor output velocity of the vehicle is 2 Hz, and the IMU data rate is 200 Hz. The RTK GPS outputs real-time differential results at 1 Hz with an accuracy of several centimetres, and is used as a position truth to evaluate the accuracy of the test results. The surroundings of the vehicle path are very complex, with a considerable amount of grass and scattered stones on the ground for most sections of the route. Some sections were bare ground.

Figure 11. Navigation platform in an experiment.
Three different methods, namely, visual odometry, IMU/WO integration, VO/IMU integration, are used for data processing using the collected data sets; a comparison of the results is also conducted. Occasional failures occur when the VO algorithm is used to compute all the image frames of the data sets. The analysis shows that solution failure occurs when the number of feature points in the image is too low, such as in highly reflective bare ground. This failure also occurs when the feature matching is difficult to perform, such as in a monotonous grass background. To fill these gaps, the IMU/wheel odometry integration is used to link the failed image frames.
Figure 12 shows the trajectories of the vehicle in the experiment; the four trajectories obtained from RTK GPS, IMU/WO integration, VO solution, and VO/IMU integration are also shown. The trajectory from the VO/IMU integration is very close to that of RTK GPS. The deviations between the RTK GPS trajectory and the three others are also found to increase with the running distance. Table 5 lists the navigation errors of the three methods. The position error of the terminal point of the VO/IMU integration is much smaller than that of the IMU/wheel odometry integration and the VO solution, with running distance of 1150 m, an accumulated error of 8·6 m, and a relative error percentage of 0·75%. During the experiment, there are six times of short-time visual odometry failure, but we can see that the accuracy of the integrated system is not seriously affected by the visual odometry failure.

Figure 12. Trajectories obtained from the different solutions.
Table 5. Solution errors compared to GPS.

The innovation of Kalman filtering is illustrated in Figure 13 and Figure 14, including position innovation and attitude innovation. It can be seen from Figure 13 that the maximum position innovation in X, Y, Z directions is less than 0·15 m, and in most cases less than 0·05 m. It can be seen from Figure 14 that the maximum attitude innovation in pitch, roll, yaw angles is less than 0·1°, and in most cases less than 0·02°. The innovation indicates that the Kalman filtering process is relatively stable, the visual odometry and IMU integrated algorithm in this paper is valid and efficient.

Figure 13. Position innovation of Kalman filtering.

Figure 14. Attitude innovation of Kalman filtering.
6. CONCLUSIONS
The current article introduces in detail the integrated vision navigation system matching concept, research background, and recent developments both domestic and abroad. The proposed passage applies a reliable estimation method that improves the matching results of the SURF method, significantly reducing the rate of wrong matches while avoiding extra calculation time. The proposed system makes use of the improved results from the SURF method as well as the relevant theories on photogrammetry. Moreover, the proposed system realizes the measurement of 3D coordinates and an image sequence-based fast coordinate extrapolation. At the same time, relevant programs are developed and applied, and experimental results are collected and analysed. Finally, the proposed system uses the integrated IMU data to further improve the accumulated error of the model, which would be the foundation for further studies.
The SURF method can execute a faster common point matching and perform real-time matching. However, several wrong matching points are still obtained, affecting the application range for the matching results. The improved SURF method not only rapidly matches the common points, it also avoids many wrong matching points, contributing to the overall accuracy. However, the improved method reduces the amount of matching points. Based on the simple and efficient 3D coordinate measurement method of the basic theory of photogrammetry, the coordinates of the image point in object space can easily be obtained. However, a number of technical problems on the measurement of the image sequence-based coordinates remain to be resolved. The IMU can provide an exterior orientation for the image, which greatly simplifies the calculation. The combined treatment of IMU data will be investigated in the future.
ACKNOWLEDGEMENT
The work in this paper is supported by National Basic Research Program of China (Project No. 2012CB957702).