2.1. Orbit dynamic model

WGS84 is selected as the reference coordinate system, and we suppose that the high order terms of disturbance caused by the Earth, Sun, Moon or atmosphere are ignored. The equations of this model are given below (Ning and Fang, Reference Ning and Fang2007):

(1)$$\left\{ \eqalign{\displaystyle{{{\rm d}x} \over {{\rm d}t}} = & v_x + w_x \cr \displaystyle{{{\rm d}y} \over {{\rm d}t}} = & v_y + w_y \cr \displaystyle{{{\rm d}z} \over {{\rm d}t}} = & v_z + w_z \cr \displaystyle{{{\rm d}v_x} \over {{\rm d}t}} = & - \mu \displaystyle{x \over {r^3}} \left[ {1 - J_2 \left( {\displaystyle{{R_e} \over r}} \right)\left( {7.5\displaystyle{{z^2} \over {r^2}} - 1.5} \right)} \right] + a_x + w_{v_x} \cr \displaystyle{{{\rm d}v_y} \over {{\rm d}t}} = & - \mu \displaystyle{y \over {r^3}} \left[ {1 - J_2 \left( {\displaystyle{{R_e} \over r}} \right)\left( {7.5\displaystyle{{z^2} \over {r^2}} - 1.5} \right)} \right] + a_y + w_{v_y} \cr \displaystyle{{{\rm d}v_z} \over {{\rm d}t}} = & - \mu \displaystyle{z \over {r^3}} \left[ {1 - J_2 \left( {\displaystyle{{R_e} \over r}} \right)\left( {7.5\displaystyle{{z^2} \over {r^2}} - 4.5} \right)} \right] + a_z + w_{v_z} \cr \displaystyle{{{\rm d}a_x} \over {{\rm d}t}} = & - \alpha _x a_x + w_{a_x} \cr \displaystyle{{{\rm d}a_y} \over {{\rm d}t}} = & - \alpha _y a_y + w_{a_y} \cr \displaystyle{{{\rm d}a_z} \over {{\rm d}t}} = & - \alpha _z a_z + w_{a_z}} \right.$$

where r represents $\sqrt {\left( {x^2 + y^2 + z^2} \right)} $, x, v _x, y, v_y, z, v_z are satellite positions and velocities on the three axes respectively; a _x, a_y, a_z are part of the perturbing accelerations on the three axes respectively which can be approximated by the Singer model; α _x, α_y, α_z are reciprocals of the correlation time constants on the three axes respectively; R _e is the earth radius; μ is the gravitational constant of the earth; J ₂ is the second zonal coefficient.

2.2. Measurement model of GPS

The theory of satellite navigation is illustrated by Figure 1.

Figure 1. Diagram of satellite navigation.

The pseudo-range between spacecraft receiver and navigation satellite is regarded as the observation of the measurement equations. To determine unknown position vectors of the target spacecraft in space, the position information of three navigation satellites needs to be obtained. Considering that the clock bias can produce a big observation error that can neither be ignored nor be predicted, the clock bias is regarded as an unknown quantity that needs to be determined. As a result, the information of a fourth navigation satellite is needed. Now, the position information of four navigation satellites need to be obtained to determine the position vectors of the target spacecraft and clock bias of receiver using the least squares method. The number of observable satellites is assumed to be four, and the measurement equations are given as follows:

(2)$$\left\{ {\matrix{ {\rho _1 = \sqrt {\left( {x^1 - x} \right)^2 + \left( {y^1 - y} \right)^2 + \left( {z^1 - z} \right)^2} + c\delta t_u + \varepsilon _1} \cr {\rho _2 = \sqrt {\left( {x^2 - x} \right)^2 + \left( {y^2 - y} \right)^2 + \left( {z^2 - z} \right)^2} + c\delta t_u + \varepsilon _2} \cr {\rho _3 = \sqrt {\left( {x^3 - x} \right)^2 + \left( {y^3 - y} \right)^2 + \left( {z^3 - z} \right)^2} + c\delta t_u + \varepsilon _3} \cr {\rho _4 = \sqrt {\left( {x^4 - x} \right)^2 + \left( {y^4 - y} \right)^2 + \left( {z^4 - z} \right)^2} + c\delta t_u + \varepsilon _4} \cr}} \right.$$

where [xⁱ, yⁱ, zⁱ]^T (i = 1, 2, 3, 4), [x, y, z]^T denote the position of observable satellites and position of spacecraft receiver in the WGS84 coordinate system respectively; c denotes the velocity of light; δt _u denotes the GPS clock bias; ρ _i (i = 1, 2, 3, 4) denotes the pseudo-range between spacecraft receiver and observable satellites; ε _i is the measurement noise and assumed to be zero-mean white noise.

Define δf _u as the clock bias drift of receiver, and δt _u is caused by the clock bias drift with the following equation:

(3)$$\dot \delta t_u = \delta f_u $$

In practice, δf _u is usually regarded as coloured noise, and can be modelled as a Markov model:

(4)$$\dot \delta f_u = - \lambda _\xi \delta f_u + s$$

where λ _ξ denotes the reciprocal of the correlation time constants for the model, s denotes the zero-mean Gaussian noise.

2.3. Autonomous navigation system model based on GPS measurement

X = [x, v _x, a_x, y, v_y, a_y, z, v_z, a_z, δt_u, δf_u]^T is regarded as the state variable of an autonomous navigation system, where δt _u and δf _u denote the clock bias and clock bias drift of GPS receiver respectively. According to Equations (1) to (4), the autonomous navigation model based on GPS measurement can be given by:

(5)$$\eqalign{{\bi \hat X} &= f\,({\bi X}) + {\bi w} \cr {\bi Z} &= h({\bi X}) + {\bi \varepsilon}} $$

where ${\bi X} \in {\opf R}^n $ and ${\bi Z} \in {\opf R}^m $ denote the state variable and observation which is comprised of the pseudo-range between target spacecraft and GPS navigation satellites; f(·) and h(·) denote the general equation of Equation (1) and Equation (2) respectively; w = (w _x, w_vx, w_ax, w_y, w_vy, w_ay, w_z, w_vz, w_az, 0, w _t)^T, ε = (ε ₁, ε ₂, ε ₃, ε ₄)^T denotes the system noise and measurement noise respectively.

3.1. PLDIs model of autonomous navigation estimation error system

${\bi \hat X}$ is assumed to be the optimal system state estimation. The system state and observed estimation satisfy:

(6)$$\eqalign{{\bi \dot {\hat X}} = f\left( {{\bi \hat X}} \right) \cr {\bi \hat Z} = h\left( {{\bi \hat X}} \right)} $$

where ${\bi \hat Z}$ denotes the observed estimation of measurement model.

The state estimation error and observed residual can be defined as:

$$\eqalign{\Delta {\bi X} = & {\bi X} - {\bi \hat X} \cr \Delta {\bi Z} = & {\bi Z} - {\bi \hat Z}} $$

Therefore, the estimation error model of autonomous navigation system can be given by:

(7)$$\eqalign{\Delta {\bi \dot X} = f\left( {\bi X} \right) - f\left( {{\bi \hat X}} \right) + {\bi w} \cr \Delta {\bi Z} = h\left( {\bi X} \right) - h\left( {{\bi \hat X}} \right) + {\bi \varepsilon}} $$

Theorem 1

Ω_x is a subset of n-dimensional space, ${\bi \Omega} _x \subseteq {\opf R}^n $, and the vector function f is defined as: ${\bi \Omega} _x \to {\opf R}^m $. If Ω_x and f satisfy the following conditions:

1. (1) f is continuously differentiable;

2. (2) The arbitrary point X and vector H at the subset Ω_x satisfy: X + α H ∈ Ω_x;

3. (3) Partial derivatives of f vary in a bounded domain belonging to ${\opf R}^{m \times n} $;

Then,

(8)$$f\left( {{\bi X} + {\bi H}} \right) - f\left( {\bi X} \right) \in Co\left( {{\bi \Omega} _f} \right){\bi H}$$

where 0 ⩽ α ⩽ 1, ${\bi H} \in {\opf R}^n $, Co(Ω_f) is the convex hull generated by Ω_f.

Proof:

The vector function $f{\hskip -2pt}:{\bi \Omega} _x \to {\opf R}^m $ is continuously differentiable. The arbitrary point X and X + H ∈ Ω_x satisfy X + α H ∈ Ω_x, thus according to differential mean value theorem of vector function (de Boor, Reference De Boor2005) we have:

(9)$$f\,({\bi X} + {\bi H}) - f\,({\bi X}) = [\int_0^1 {\nabla f\,({\bi X} + \alpha {\bi H}){\rm d}\alpha} ]{\bi H}$$

where ∇f is the partial derivative of f, namely, the Jacobian matrix of f. Therefore,

(10)$$f_i ({\bi X} + {\bi H}) - f_i ({\bi X}) = \int_0^1 {\sum\limits_{\,j = 1}^n {\left[\displaystyle{{\partial f_i} \over {\partial x_j}} ({\bi X} + \alpha {\bi H})h_j\right ]} {\rm d}\alpha} $$

where i = 1, 2···m. Because partial derivatives of f vary in a bounded domain belonging to ${\opf R}^{m \times n} $, the value of each element in ∇f is bounded, and can be expressed as:

(11)$$\eqalign{\nabla f_{{\rm ij}} = & \displaystyle{{\partial f_i} \over {\partial x_j}} \cr \nabla f_{{\rm ij}}^{\max} = & \max \left( {\nabla f_{{\rm ij}} \left( {{\bi X} + \alpha {\bi H}} \right)} \right) \cr \nabla f_{{\rm ij}}^{\min} = & \min \left( {\nabla f_{{\rm ij}} \left( {{\bi X} + \alpha {\bi H}} \right)} \right)} $$

∇f _ij can also be expressed as:

(12)$$\nabla f_{{\rm ij}} ({\bi X} + \alpha {\bi H}) = \lambda _1 \nabla f_{{\rm ij}}^{\max} + \lambda _2 \nabla f_{{\rm ij}}^{\min} $$

where,

(13)$$\eqalign{\lambda _1 = & \displaystyle{{\nabla f_{{\rm ij}} ({\bi X} + \alpha {\bi H}) - \nabla f_{{\rm ij}}^{\min}} \over {\nabla f_{{\rm ij}}^{\max} - \nabla f_{{\rm ij}}^{\min}}} \cr \lambda _2 = & \displaystyle{{\nabla f_{{\rm ij}}^{\max} - \nabla f_{{\rm ij}} ({\bi X} + \alpha {\bi H})} \over {\nabla f_{{\rm ij}}^{\max} - \nabla f_{{\rm ij}}^{\min}}}} $$

When ∇f _ij^max = ∇f _ij^min, one of λ ₁ and λ ₂ can be assumed to be 1 and the other is assumed to be 0. As a result, the above equation holds. According to the above equation, ranges of λ ₁ and λ ₂ are 0 ⩽ λ ₁ ⩽ 1, 0 ⩽ λ ₂ ⩽ 1. Therefore, according to Equation (12):

(14)$$\nabla f_{{\rm ij}} ({\bi X} + \alpha {\bi H}) \in Co(\nabla f_{{\rm ij}}^{\max}, \nabla f_{{\rm ij}}^{\min} )$$

The following equation can be given by substituting the above equation into Equation (10):

(15)$$f_i \left( {{\bi X} + {\bi H}} \right) - f_i \left( {\bi X} \right) \in \int_0^1 {\sum\limits_{\,j = 1}^n {\left[ {Co(\nabla f_{{\rm ij}}^{\max}, \nabla f_{{\rm ij}}^{\min} )h_j} \right]} {\rm d}\alpha} $$

Let Ω_i be Ω_i = {a|a _j ∈{∇f _ij^max, ∇f _ij^min}, j = 1, 2···n}, namely, each point at set Ω_i is ${\bi a} \in {\opf R}^n $, a _j is the n-th element of a and its value is ∇f _ij^max or ∇f _ij^min. Thus, the above equation can also be expressed as:

(16)$$f_i \left( {{\bi X} + {\bi H}} \right) - f_i \left( {\bi X} \right) \in \int_0^1 {Co\left( {{\bi \Omega} _{\bi i}} \right){\bi H}} {\rm d}\alpha $$

Considering that the integral term is irrelevant to α, the above equation is equivalent to:

(17)$$f_i \left( {{\bi X} + {\bi H}} \right) - f_i \left( {\bi X} \right) \in Co\left( {{\bi \Omega} _i} \right){\bi H}$$

The above equation shows that each row in the Jacobian matrix of f can be expressed in the form of differential inclusion, $\displaystyle{{{\rm \partial} f_i} \over {\partial {\bi X}}} = Co({\bi \Omega} _i )$. The left side of Equation (9) can also be expressed as:

(18)$$\eqalign{\,f\left( {{\bi X} + {\bi H}} \right) - f\left( {\bi X} \right) &= \sum\limits_i^m {\left( {\,f_i \left( {{\bi X} + {\bi H}} \right) - f_i \left( {\bi X} \right)} \right)} {\bi I}_{m \times 1}^i \cr & \in \sum\limits_i^m {\left[ {Co({\bi \Omega} _i ){\bi H}} \right]} {\bi I}_{m \times 1}^i} $$

Where ${\bi I}_{m \times 1}^i $ denotes the i-th unit of space ${\opf R}^{m \times 1} $ whose elements are all 1. According to Equation (17), the above equation is equivalent to:

(19)$$f\left( {{\bi X} + {\bi H}} \right) - f\left( {\bi X} \right) \in Co\left( {{\bi \Omega} _f} \right){\bi H}$$

where Ω_f = {a|a _ij ∈ {∇f _ij^max, ∇f _ij^min}, i= 1, 2···m; j = 1, 2···n} means that each point in Ω_f is ${\bi a} \in {\opf R}^{m \times n} $, and the value of element in a, a _ij, is ∇f _ij^max or ∇f _ij^min.

QED.

According to Theorem 1, the estimation error system represented by Equation (7) can be expressed as:

(20)$$\eqalign{& \Delta {\bi \dot X} \in Co({\bi \Omega} _f )\Delta {\bi X} + {\bi w} \cr & \Delta {\bi Z} \in Co({\bi \Omega} _h )\Delta {\bi X} + {\bi \varepsilon}} $$

Theorem 2

Considering the nonlinear system represented by Equation (5), if f(·), h(·) are both continuously differentiable and the value set of the Jacobian matrices is a bounded set, the estimation error system can be modelled as follows:

(21)$$\eqalign{\Delta {\bi \dot X} = {\bi A}\Delta {\bi X} + {\bi w} \cr \Delta {\bi Z} = {\bi C}\Delta {\bi X} + {\bi \varepsilon}} $$

where matrix A and matrix C are defined as:

$$({\bi A},{\bi C}) = \sum\limits_{i = 1}^l {\lambda _i ({\bi A}_i, {\bi C}_i )} $$

where λ _i are weights of convex combination, and 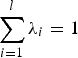$\sum\limits_{i = 1}^l {\lambda _i} = 1$, 0 ⩽ λ _i ⩽ 1, A_i and C_i are system vertex matrices of the PLDIs model; l is number of the system vertex matrices.

Proof:

The estimation error system represented by Equation (7) can be expressed as:

(22)$$\left( {\matrix{ {\Delta {\bi \dot X}} \cr {\Delta {\bi Z}} \cr}} \right) = \left( {\matrix{ {\,f\left( {{\bi \hat X} + \Delta {\bi X}} \right)} \cr {h\left( {{\bi \hat X} + \Delta {\bi X}} \right)} \cr}} \right) - \left( {\matrix{ {\,f\left( {{\bi \hat X}} \right)} \cr {h\left( {{\bi \hat X}} \right)} \cr}} \right) + \left( {\matrix{ {\bi w} \cr {\bi \varepsilon} \cr}} \right)$$

For a nonlinear filtering algorithm with good estimation performance, the difference between state estimation and real state of system, ΔX, tends to be zero or very small. As a result, we can find a proper subset ${\bi \Omega} _x \subset {\opf R}^n $ which includes ${\bi \hat X}$ and ${\bi \hat X}$ + αΔX, where 0 ⩽ α ⩽ 1. Considering that nonlinear functions f(·), h(·) are both continuously differentiable and partial derivatives of them vary in a bounded domain, the above estimation error system can be expressed as:

(23)$$\left( {\matrix{ {\Delta {\bi \hat X}} \cr {\Delta {\bi Z}} \cr}} \right) \in Co\left( {{\bi \Omega} _{{\rm fh}}} \right)\Delta {\bi X} + \left( {\matrix{ {\bi w} \cr {\bi \varepsilon} \cr}} \right)$$

Where ${\bi \Omega} _{{\rm th}} \subset {\opf R}^{(m + n) \times n} $ is the value set of partial derivative of nonlinear function g (X) = (f(X)^T h (X)^T)^T with respect to the system state variable. The above equation represents a Linear Differential Inclusion system (LDIs). In general, Co(Ω_fh) can be approximated by an endo-tangent polytope with any accuracy (Xie et al., Reference Xie, Soh and Du2005; Li, Reference Li2002). Therefore, there will always be a polytope Ω satisfying:

(24)$$Co\left( {{\bi \Omega} _{{\rm fh}}} \right) \approx {\bi \Omega} = \left\{ {\left. {\left( {\matrix{ {\bi A} \cr {\bi C} \cr}} \right)} \right|\left( {\matrix{ {\bi A} \cr {\bi C} \cr}} \right) = \sum\limits_{i = 1}^l {\lambda _i \left( {\matrix{ {{\bi A}_i} \cr {{\bi C}_i} \cr}} \right)}, 0 \les \lambda _i \les 1} \right\}$$

Thus, Equation (23) can be expressed in the form of Equation (21).

QED.

According to Theorem 1, Theorem 2 and the autonomous navigation estimation error system indicated by Equation (7), an estimation error system can be modelled as the PLDIs model. According to the TP model transformation (Baranyi, Reference Baranyi2004), the PLDIs model can be determined by the following steps:

Step 1: Determine the bound domain Ω_p. Considering that parameters included by the Jacobian matrices are positions on three axes, x, y, z, Ω_p can be expressed as Ω_p = [c ₁, d ₁] × [c ₂, d ₂] × [c ₃, d ₃].

Step 2: Divide Ω_p into I _n grids uniformly distributed on each dimensionality: ${\bi p}_n \in \{ {\bi p}_{n,1} ,{\bi p}_{n,2} ,\cdots {\bi p}_{n,I_n } \} $ where $c_n \les p_{n,1} \les p_{n,2} \cdots \les p_{n,I_n } \les d_n ,n = 1,2,3;$

Step 3: Sample the functions S(p_n,_in) over the hyper rectangular grid and store the sample matrices in the tensor S;

Step 4: Execute the Higher Order Singular Value Decomposition (HOSVD) on each dimensionality of tensor S, and discard not only zero n-mode singular values but also part of the non-zero n-mode singular values. Normalised n-mode matrices U_n, and tensor S are approximated by: ${\bi \hat S} = {\bi \bar G}^{\prime} \mathop \otimes \limits_{n = 1}^3 {\bi \bar U}_n^{\prime}$

Step 5: Extract the vertex matrices C_j for the PLDIs model from ${\bi \bar G}'$.

The vertex systems of autonomous navigation system which is modelled as a PLDIs model are determined by TP model transformation. It means that the Jacobian matrix is expressed in the form of convex combination, which is composed by a variety of constant matrices. S(p) is defined as a matrix composed by Jacobian matrices:

$${\bi S}({\bi p}) = \left( {\displaystyle{{\partial h} \over {\partial {\bi X}}}} \right),{\bi p}{\rm =} {\bi X}$$

According to TP model transformation, S(p) can be approximately expressed in the form of convex combination, composed by a variety of constant matrices.

(25)$${\bi S}\left( {\bi p} \right) \approx \sum\limits_{i = 1}^l {\lambda _i \left( {\bi p} \right){\bi S}_i} = \sum\limits_{i = 1}^l {\lambda _i \left( {\bi p} \right){\bi C}_i} $$

where λ _i (p) are weights of convex combination, and 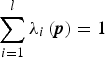$\sum\limits_{i = 1}^l {\lambda _i \left( {\bi p} \right)} = 1$, 0 ⩽ λ _i(p) ⩽ 1, C_i is the constant matrices.

Therefore, the autonomous navigation estimation error system can be described by a PLDIs model as follows:

(26)$$\eqalign{& {\rm \Delta} {\bi \dot X = \Phi} {\rm \Delta} {\bi X + B\upsilon} \cr & {\rm \Delta} {\bi Z = C}{\rm \Delta} {\bi X + D\upsilon}} $$

where

$$\eqalign{& {\bi B}\,=\,\left[ {{\bi I}_{11 \times 11}\,0_{11 \times 4}} \right],{\bi D} = \left[ {0_{4 \times 11}\,{\bi I}_{4 \times 4}} \right],\,{\bi \upsilon} = \left[ \matrix{{\bi w} \cr{\bi \varepsilon} } \right] \cr & {\bi C} \in \left\{ {\left. {\bi C} \right|{\bi C} = \sum\limits_{\,j = 1}^l {\lambda _j {\bi C}_j, 0} \les \lambda _j \les 1,\sum\limits_{\,j = 1}^l {\lambda _j} = 1} \right\}} $$

where C_j denotes the j-th vertex system matrices, and C_j is constant matrix; l is number of the vertex system matrices.

3.2. Spacecraft autonomous navigation algorithm

The PLDIs model of spacecraft autonomous navigation system is determined by TP model transformation as above, and the PKF algorithm will be given by following steps based on the above results.

Forecast states:

(27)$${\bi \hat X}_{k/k - 1} = {\bi \Phi} _{k/k - 1} {\bi \hat X}_{k - 1} $$

(28)$${\bi \hat P}_{k/k - 1} = {\bi \Phi} _{k/k - 1} {\bi \hat P}_{k - 1} \left( {{\bi \Phi} _{k/k - 1}} \right)^T + {\bi Q}_k $$

(29)$$\Delta {\bi Z}_k = {\bi Z}_k - {\bi \hat Z}_k = {\bi Z}_k - h\left( {{\bi \hat X}_{k/k - 1}} \right)$$

(30)$${\bi K}_{\,j,k} = {\bi \hat P}_{k/k - 1} {\bi C}_j ^T \left( {{\bi C}_j {\bi \hat P}_{k/k - 1} {\bi C}_j ^T + {\bi R}_k} \right)^{ - 1} $$

Update estimation error covariance matrix: Different estimation error covariance matrices are obtained by different gains K_j,k and C_j, and the global estimation error covariance matrix is obtained according to data fusion.

(31)$${\bi \hat P}_{\,j,k} = \left( {{\bi I}_n - {\bi K}_{\,j,k} {\bi C}_j} \right){\bi \hat P}_{k/k - 1} \left( {{\bi I}_n - {\bi K}_{\,j,k} {\bi C}_j} \right)^T + \, {\bi K}_{\,j,k} {\bi R}_k {\bi K}_{\,j,k} ^T $$

(32)$${\bi \hat P}_k^{ - 1} = {{\sum\limits_{j = 1}^l {s_j \left( {{\bi \hat P}_{j,k}} \right)^{ - 1}}} \Big/ {\sum\limits_{j = 1}^l {s_j}}} $$

Calculate correcting value of state estimation: Different correcting values are obtained for different gains K_j,k, and the global correcting value can be given according to data fusion.

(33)$$\Delta {\bi \hat X}_{\,j,k} = {\bi K}_{\,j,k} \Delta {\bi Z}_k $$

(34)$$\Delta {\bi \hat X}_k = {{\sum\limits_{j = 1}^l {\left( {s_j \Delta {\bi \hat X}_{j,k}} \right)}} \Big/ {\sum\limits_{j = 1}^l {s_j}}} $$

Update state estimation:

(35)$${\bi \hat X}_k = {\bi \hat X}_{k/k - 1} + \Delta {\bi \hat X}_k $$

where j = 1…l, s _j denotes the j-th n-mode singular matrix of the n-mode matrix. The PKF navigation algorithm proposed in this section takes the place of EKF. The difference between the nonlinear filtering algorithm used by PKF navigation algorithm and that used by EKF navigation algorithm is that the Jacobian matrix is represented by convex combination composed by a variety of constant matrices. Compared with EKF, the algorithm proposed needs not to update the Jacobian matrix online and the algorithm design is simpler.