2. GEOMETRIC OBSERVERS

The search for a less demanding estimation method than Kalman filtering has led to the invention of a group of techniques which we call geometric observers. What they all have in common is that the estimates of all desired variables are expressed only in terms of quantities with clear geometrical meaning. These observers make use of three-dimensional vectors in conventional Euclidean space, and no multidimensional vector-matrix operations are needed.

3. BIAS OBSERVER DESIGN

We start the observer construction with several assumptions that are reasonable in the context of precision agriculture applications:

1. A) The IMU is subjected to factory calibration, so the residual sensor biases are small, as well as the attitude errors caused by these biases.

2. B) Farming machines typically move on nearly flat terrain, so the roll and pitch angles and the corresponding angular rates are small; vertical accelerations are negligible compared with gravity.

3. C) The vehicle does not suffer from sideslip and the GNSS signals are not blocked by any obstacles, so the heading angle is perfectly known as the direction of the vehicle velocity measured by the GNSS receiver.

4. D) The effects of Earth's rotation and curvature are not taken into consideration.

Now, if we neglect all the products of at least two small values, we can arrive at a linearized error dynamics model, from which the bias observer structure can be deduced and its stability proven. Any possible violations of our assumptions, e.g., during the motion on a hill slope, will not necessarily impair the practical performance of the observer but will of course invalidate its theoretical justifications.

A serious challenge in the observer construction is to decide what available quantities are suitable to drive the observer. The most obvious choice is to use the raw measurements provided by the IMU and the GNSS receiver. Unfortunately, they are coupled with the sensor biases through several complicated differential equations (Titterton and Weston, Reference Titterton and Weston2004), and this choice returns us to the implementation problems we wished to avoid. Then, following the guidelines of the geometric observers theory, we select the control angular rate to drive the bias observer. So we now need to find how this angular rate is coupled with the quantities of interest, i.e., with gyro and accelerometer biases.

3.1. Attitude Dynamics

Consider a strapdown AHRS that computes the direction cosine matrix C between the body frame b = {x _b, y_b , z_b} and the “virtual platform” frame p = {x _p, y_p, z_p}. The body frame is chosen such that x _b points forwards, y _b rightwards, z _b downwards. The “virtual platform” frame is slightly misaligned from the North-East-Down frame n = {N, E, D}.

The matrix dynamics are described by the equation (Salychev, Reference Salychev2004)

(1)$$\dot{\bf C} = {\bf C} \breve{{\bf \omega}}_b^b - \breve{{\bf \omega}}_p{\hskip-3pt^p} {\bf C}$$

Here a subscript denotes the frame for which the angular rate is specified, and the superscript denotes the frame to which the rate is projected. Thus, ω_b^b is the body frame angular rate as measured by the gyros, ω_p^p is the “virtual platform” control angular rate as seen from this “virtual platform”. An arc denotes a skew-symmetric matrix corresponding to a vector, so that $ {\breve{\bf a} \bf b} = {\bf a \times b}$.

Let us project the accelerometer measurements f_b onto the “virtual platform”:

(2)$${\bf f}_p = {\bf Cf}_b $$

For a perfect AHRS installed on a vehicle that moves on a flat non-rotating Earth (Assumption D), the “virtual platform” lies in the local level plane, so that f_p = f_n. Therefore, the first two components of f_p = [f _N, f_E, f_D]^Tcontain only the actual accelerations, but not the projections of the gravity vector g. If this ideal condition is violated and the “virtual platform” is not horizontal, there appears a difference between the measured specific force f_p and the true specific force ${\bf f}_n ^{GNSS} = \dot {\bf v}_n ^{GNSS} - {\bf g}$. The latter is provided by differentiating the vehicle velocity v_n^GNSS measured by the GNSS receiver. The difference is fed back to the “virtual platform” in the form of the control angular rate:

(3)$${\bf \omega}_p{\hskip-3pt^p} = - \breve{{\bf k}} _p ({\bf f}_n^{GNSS} - {\bf f}_p )$$

Here the vertical vector k = −k g/g represents the attitude correction gain, and the quantity τ = 1/(kg) is the correction time constant. Since in the perfect case ω_p^p = 0, any variation of this angular rate is equal to the rate itself: δ ω_p^p = ω_p^p.

3.2. Attitude Error Dynamics

In the presence of gyro and accelerometer biases, b_g and b_a, the “virtual platform” tilt error θ appears. This error is small due to Assumption A, so we are able to represent it by a vector and express the direction cosine matrix variation as $\delta {\bf C} = \breve{{\bf \theta}}_p^p {\bf C}$. By varying Equation (1) and substituting δ ω_b^b = b_g and δ ω_p^p = ω_p^p, we can get

(4)$$\dot {\bf \theta}_p^p = {\bf Cb}_g - {\bf \omega}_p^p $$

Equation (4) has a clear physical meaning. The rate of change of the attitude error vector is determined by two opposite factors: the gyro biases (projected onto the “virtual platform”) and the control angular rate. However, this equation is not convenient for the analysis of strapdown AHRS performance, since its terms are not constant during the vehicle turns. Instead, they are modulated by the C matrix, even if the sensor biases, b_g and b_a, are constant by themselves. To avoid this problem, Equation (4) can be transformed to the body frame:

(5)$$\dot {\bf \theta} _b^b + \breve{{\bf \omega}}_b^b {\bf \theta} _b = {\bf b}_g - {\bf \omega} _p^b $$

It is the last term ω_p^b = C^Tω_p^p that will be used for the estimation of inertial sensor biases. The relation between ω_p^b and b_g is already given by Equation (5). To establish a similar relation between ω_p^b and b_a, we vary Equation (2) with δ f_b = b_a:

(6)$$\delta {\bf f}_p = \;\breve{{\bf \theta}}_p^p {\bf f}_p + {\bf Cb}_a $$

Then we substitute Equation (6) into Equation (3):

(7)$${\bf \omega} _p{\hskip-3pt^p} = \breve{{\bf k}} _p \breve{{\bf \theta}}_p^p {\bf f}_p + \breve{{\bf k}} _p {\bf Cb}_a \; = \left( {{\bf k}_p^T {\bf f}_p}\right)\;{\bf \theta} _p - \left( {{\bf k}_p^T {\bf \theta} _p}\right)\;{\bf f}_p + \breve{{\bf k}} _p {\bf Cb}_a $$

The first term in the right-hand side of Equation (7) is proportional to the attitude error θ we wish to mitigate. It provides the desired error feedback that justifies our choice of the control law (Equation (3)). According to Assumption B, vertical accelerations are small, so f _D = −g and k_p^Tf_p = kg. The second term is an additional error that appears when the vectors k and θ are not orthogonal. Due to Assumption C, there is no heading error and only attitude errors are present. Then, θ lies in the level plane, while k is always vertical by its definition, so the whole term vanishes. The third term reflects the influence of accelerometer biases on the attitude correction accuracy. Though generally harmful, this term allows for the estimation of accelerometer biases by means of the ω_p^b signal. As stated in Assumption B, roll and pitch angles are small, so we can freely replace k_b by k_p and treat this vector as constant in any vehicle manoeuvres.

After accepting these simplifications and transforming Equation (7) to the body frame, we finally get

(8)$${\bf \omega} _p^b = kg\;{\bf \theta} _b + \breve{{\bf k}} _p {\bf b}_a $$

Equations (5) and (8) completely determine the attitude error dynamics and relate it to the sensor biases and to the “virtual platform” control angular rate.

3.3. Control Rate Dynamics

The attitude error by itself is neither measurable nor important for estimation. From our control law (Equation (3)) we know that, once sensor biases are estimated and compensated, the attitude error tends to zero. So it is expedient to eliminate this quantity from the final equations. First, we differentiate Equation (8), provided that b_a is constant, and get $\dot {\bf \omega} _p^b = kg\;\dot {\bf \theta} _b^b $. Second, we substitute Equation (8) and its derivative into Equation (5):

(9)$$\dot {\bf \omega}_p^b = - \left( {\breve{{\bf \omega}}_b^b + kg{\bf I}} \right){\bf \omega}_p^b + kg{\bf b}_g + \breve{{\bf \omega}}_b^b \breve{{\bf k}}_p {\bf b}_a $$

The vector triple product in the last term of Equation (9) can be significantly simplified if we utilise Assumption B and set ω_b^b = [0, 0, ω _zb]^T. Then, $\breve{{\bf \omega}} _b^b \breve{{\bf k}} _p {\bf b}_a = k\omega _{zb} {\bf b}_a $, so the product is collinear with b_a. Further, we recall the definition of the attitude correction time constant τ = 1/(kg) and rewrite Equation (9) in the form

(10)$$\tau \dot {\bf \omega}_p^b = - \left( {\tau \breve{{\bf \omega}}_b^b + {\bf I}} \right){\bf \omega}_p^b + {\bf b}_g + \omega _{zb} {\bf b}_a /g$$

The eigenvalues of the dynamics matrix $ - \left( {\tau \breve{{\bf \omega}} _b^b + {\bf I}} \right)$ are −1 and−1 ± iτω _zb. Therefore, the solution of Equation (10) is always stable.

This is exactly what we desired to obtain. Equation (10) describes a linearized coupling between sensor biases and control angular rate applied to the “virtual platform”. We will use it to justify the bias observer structure.

3.4. Bias Estimate Dynamics

The individual observers for gyro and accelerometer biases will be both driven by the control angular rate ω_p^b multiplied by some scalar gains. The choice of these gains should respect the observability conditions imposed by the nature of the system under study. In the Introduction we noticed that accelerometer biases are completely unobservable in a straight motion. This conclusion is confirmed by Equation (10). As far as ω _zb = 0, the control angular rate ω_p^b is by no means affected by accelerometer biases. Therefore, we will set the accelerometer bias observer gain proportional to the vehicle angular rate ω _zb.

Our observer equations finally take the form:

(11)$${\dot {\hat {\bf b}}}_g = {\bf \omega}_p^b /\tau_g $$

(12)$${\dot {\hat{\bf b}}}_a = g \omega_{zb} {\bf \omega}_p^b /\omega_a $$

Here, τ _g can be called the gyro bias observer time constant, and ω _a, by analogy, the accelerometer bias observer “rate constant”. These quantities play the role of adjustable parameters of the observers. They determine the settling time and the noise level of the obtained estimates.

At this stage, having derived the general observer equations, we can construct the estimation block diagram (Figure 1).

Figure 1. Bias Observer Block Diagram.

As seen from Equation (3), the bias observer requires the derivative of the measured velocity v_n^GNSS. It is generally admitted that numerical differentiation, when applied to real-world signals, results in large noise levels. Nevertheless, GNSS receivers are capable of providing quite smooth velocity measurements based on carrier phase raw data, even if the receiver position is updated using much noisier pseudorange information (Farrell and Barth, Reference Farrell and Barth1999). Since the observer does not rely on position measurements, its accuracy is enough for our particular purposes (Section 4).

3.5. Stability

When the current bias estimates are fed back to the input of the attitude observer, as shown in Figure 1, the residual sensor biases affecting the attitude accuracy are expressed as ${\bf b}_g = {\bf b}_g (0) - \hat{\bf b}_g $ and ${\bf b}_a = {\bf b}_a (0) - \hat{\bf b}_a $. The complete linearized closed-loop dynamics of these biases is determined by Equations (10) – (12) and admits the trivial zero solution. To prove its stability, we can construct a positive-definite candidate Lyapunov function:

(13)$$V = \displaystyle{\tau \over 2}\left\vert {{\bf \omega} _p^b}\right\vert^2 + \displaystyle{{\tau _g}\over 2}\left\vert {{\bf b}_g}\right\vert^2 + \displaystyle{{\omega _a}\over {2g^2}} \left\vert {{\bf b}_a}\right\vert^2 $$

Its time derivative according to dynamics equations is

(14)$$\dot V = - {\bf \omega} _p^{b\;T} \left( {\tau \breve{{\bf \omega}}_b^b + {\bf I}} \right){\bf \omega} _p^b $$

This quadratic form is negative-definite due to the specific properties of the matrix $ - \left( {\tau \breve{{\bf \omega}} _b^b + {\bf I}} \right)$ pointed out in Section 3.3. Therefore, V approaches its minimum value at the origin as long as f_p ≠ f_n^GNSS, and the trivial solution of Equations (10) – (12) is stable.

3.6. Steady-State Operation

Suppose that the vehicle is moving straight. The open-loop solution ω_p^b of Equation (10) will eventually converge to its steady value such that $\dot {\bi\omega} _{\bi p} ^{\bi b} = {\bf 0}$. Equation (10) will then take the simplest possible form

(15)$${\bf b}_g = {\bf \omega} _p^b $$

This result is in agreement with what was said in Section 2.2. The control angular rate merely compensates the gyro bias and can be directly used to estimate it.

Now suppose that the gyro bias has already been estimated and compensated, and the vehicle is turning at some constant angular rate ω _zb. Then from the steady-state solution of Equation (10) we get:

(16)$${\bf b}_a = \displaystyle{g \over {\omega _{zb}}} \left( {\tau \breve{{\bf\omega}}_b^b + {\bf I}} \right){\bf \omega} _p^b = g\left[ {\matrix{ {1/\omega _{zb}}& { - \tau}& 0 \cr \tau & {1/\omega _{zb}}& 0 \cr 0 & 0 & 0 \cr}} \right]{\bf \omega} _p^b $$

Unfortunately, Equation (16), first obtained in our previous paper (Tereshkov, Reference Tereshkov2013) without considering the general observer Equations (10) – (12), is of very limited engineering importance. Indeed, the steady-state conditions are satisfied only when the vehicle angular rate ω _zb is maintained constant for a time interval three to five times longer than the attitude correction time constant τ. Typical turns performed by land vehicles are significantly shorter, so the application of Equation (16) is not justified by practice. The general observer seems to be preferable over its elegant but unreliable steady-state solutions.

4. EXPERIMENTAL VALIDATION

The bias observer discussed in Section 3.4 was implemented in the special experimental firmware of a Topcon AGI-4 GNSS/IMU integrated receiver. The receiver was installed on the cabin roof of a MacDon 9300 self-propelled windrower (Figure 2). The windrower was driven along a curved path (Figure 3) so that the observability of both gyro and accelerometer biases was achieved.

Figure 2. MacDon 9300 Self-Propelled Windrower with Topcon AGI-4 GNSS/IMU Receiver.

Figure 3. Test Path.

To assess the observer accuracy, test run data were post-processed in two stages. At the first stage, the actual gyro and accelerometer biases for the longitudinal and lateral axes were estimated by the proposed observer and then compensated. Bias values were found to be b _gx = −0·08 deg/s, b _gy = −0·13 deg/s, b _ax = −0·11 m/s², b _ay = 0·00 m/s², which is typical for the consumer-grade MEMS sensors installed in the AGI-4 receiver. Nevertheless, these values by themselves cannot give any information regarding the bias observer performance. Since any other in-run bias estimation methods could have their own performance issues, none of them could serve as a reliable reference. For that reason, the second data processing stage was needed: the precisely known artificial biases were added to the sensor measurements, and the estimation procedure was repeated. The resulting bias estimates are shown in Figures 4 and 5.

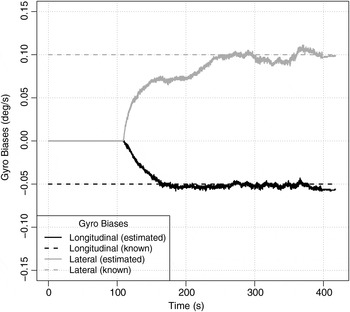
Figure 4. True and Estimated Gyro Biases.

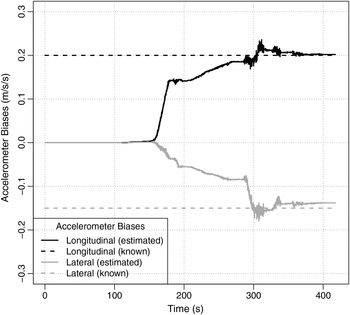
Figure 5. True and Estimated Accelerometer Biases.

Data post-processing was performed with the following observer parameter values: τ = 4 s, τ _g = 40 s, ω _a = 45 deg/s. The values were selected manually, but, in contrast to Kalman filter tuning, this was a straightforward task, as the bias observer performance is completely determined by these three constants with a rather clear and natural meaning (Section 3.4).

After the initial convergence is complete, the residual estimate variations are of the order of $\tilde b_g = 0\!\cdot \! 01\;{\rm deg/s}$ and $\tilde b_a = 0\!\cdot \!01\;{\rm m/s}^{\rm 2} $, which can be attributed partly to observer imperfections and partly to the actual uncompensated in-run bias instabilities correctly tracked by the observer. Consider the worst case when the estimate variations are solely due to observer errors. Let the vertical displacement of the GNSS/IMU integrated receiver from the vehicle “reference point” be h = 3 m, as in the example discussed in the Introduction. Then, the “reference point” positioning errors caused by the wrong attitude determination are $h\tilde b_g \tau = 2\;{\rm mm}$ and $h\tilde b_a /g = 3\;{\rm mm}$ respectively. It is by one order of magnitude less than the GNSS receiver positioning errors even in the RTK mode.

The bias observer proved to be quite robust against parameter variations: a 20 % change in any of the three adjustable constants leads to bias estimate deviations smaller than 0·001deg/ s and 0·01 m/ s².