1. INTRODUCTION
Space debris are man-made objects, which have existed in space since the first launch of artificial satellites. This includes satellites whose operational lifespan is over, components of rockets and other objects. Space debris is a major in-space operational hazard for both current and future satellites and manned missions. Therefore, it is rapidly becoming necessary to consider cleaning up potential orbits from any debris. The first stage of this is to precisely detect the orbits of debris (Flury, Reference Flury1995). Orbit determination (Armellin et al., Reference Armellin, Lizia and Zanetti2016; Curtis, Reference Curtis2013) is germane to one of the branches of astronomy, which observes, calculates and predicts space objects' orbits. One common application of orbit determination is supporting Global Positioning System (GPS) satellites (Montenbruck et al., Reference Montenbruck, Gill and Kroes2005) Andres Johan Lexell and Friedrich Gauss initiated modern orbit determination (Sten and Aspaas, Reference Sten and Aspaas2013). Furthermore, Gauss introduced a technique through which six orbital elements are obtained through only three observations at three different times (Chung, Reference Chung2006). For orbit determination, using Gauss's Method, right ascension and declination should be specified during three different times. Moreover, local sidereal time is also specified at the observation times. This technique is specific to short arcs; in other words, the time difference between two observations should be shortened (Fadrique et al., Reference Fadrique, Maté, Grau, Sánchez and García2012). One of the other methods for Angles-only Orbit Determination is the Laplace Method, which is a standard technique for initial orbit calculations. This method was used for the first time for the orbit determination of a meteor named P/1846 D1. The Laplace method is similar to the Gauss technique (Richard, Reference Richard2003).
Another method for orbit determination is Gooding's (Reference Gooding1993) method that considered various issues, the first of which is about the best position and time for observation of space objects. The second point pertaining to his work is utilisation of auxiliary sensory tools with the purpose of improving the observation conditions. Moreover, the effects of sensor type and their accuracy for initial distance determination were considered in the method. Further methods incorporate a myriad of corrections on the Laplace and Gauss methods. Briggs and Slowley (Reference Briggs and Slowley1959) presented a technique through which an iterative method was introduced utilising computer technologies. Escobal (Reference Escobal1965) has presented an approach for angles-only orbit determination, namely the Double Iteration Method. This technique is similar to the classical orbit determination methods; however, there are some differences between them. For instance, Escobal's approach is far more accurate than previous classical methods, but compared to the previous ones, the method suffers from long computational time. Vallado (Reference Vallado2010) has recently considered the three basic techniques including Gauss, Laplace and Escobal, and proposed these mentioned methods as the standard orbit determination techniques. All the Gauss, Laplace, Gooding and Escobal methods focus on angles. The Gooding method is an extended iterative technique that is specific to earth-orbiting satellites, where their angular data are based on several rotations around the earth. This method is not compatible with our objectives in this work. On the other hand, Escobal's technique, that is Double Iteration, is suitable for long arcs.
The Laplace approach will be optimal only if the distance between the grabber satellite and space debris is extremely long. Therefore, the best method for short arcs, which is the main objective of this paper, is the Gauss approach (Marsden, Reference Marsden1985). In addition, Xu et al. (Reference Xu, Hu and Jiang2016) achieved some rendezvous by the proposed adaptive control based on the measurements of relative position and velocity between the chaser and target spacecraft. Gruntman (Reference Gruntman2014) researched some methods that use optical methods for detecting sub millimetre and millimetre size debris in low earth orbits. In addition, some further research on extensions of these methods has also been conducted in Armellin et al. (Reference Armellin, Lizia and Zanetti2016) and Kaufman et al. (Reference Kaufman, Lovell and Lee2016) for further analysis of the uncertainties. Figure 1 exhibits the proposed plan of robust in-orbit localisation and orbit prediction of the space debris.

Figure 1. Diagram of robust in-orbit positioning, orbit determination, and path prediction.
2. ITERATIVE BEARING-ONLY POSITIONING OF SPACE DEBRIS
All the orbit determination methods are based on a common basis (Townsend, Reference Townsend2008). If
![]() $\vec{\bi r}$
is position vector of the space debris,
$\vec{\bi r}$
is position vector of the space debris,
![]() $\vec{\bi{\rho}}$
is the distance vector between the space debris and grabber satellite and
$\vec{\bi{\rho}}$
is the distance vector between the space debris and grabber satellite and
![]() $\vec{\bi R}$
is position vector of grabber satellite, it leads to:
$\vec{\bi R}$
is position vector of grabber satellite, it leads to:
where
![]() $\hat{L}$
is direction unit vector between the space debris and grabber satellite. A schematic view of the problem's geometry for orbit determination of space debris is displayed in Figure 2 For calculating the position vector of the space debris, it is necessary to present some assumptions in this paper. Since the main goal of this work is utilisation of a low-cost orbit determination based on the observations from an orbiting robot; this work is limited to utilising bearing-only methods. In other words, since finding the slant range between the space debris and grabber satellite needs expensive equipment, the Gauss technique, which is one of the bearing-only methods, is employed in this research (Curtis, Reference Curtis2013). Therefore, the azimuth and elevation angles between the observer and debris are specified. Note that the following angles are related to three different times over a short arc. For orbit determination using the Gauss method, the obtained azimuth and elevation angles are first converted into right ascension and declination, which are shown in Figure 3.
$\hat{L}$
is direction unit vector between the space debris and grabber satellite. A schematic view of the problem's geometry for orbit determination of space debris is displayed in Figure 2 For calculating the position vector of the space debris, it is necessary to present some assumptions in this paper. Since the main goal of this work is utilisation of a low-cost orbit determination based on the observations from an orbiting robot; this work is limited to utilising bearing-only methods. In other words, since finding the slant range between the space debris and grabber satellite needs expensive equipment, the Gauss technique, which is one of the bearing-only methods, is employed in this research (Curtis, Reference Curtis2013). Therefore, the azimuth and elevation angles between the observer and debris are specified. Note that the following angles are related to three different times over a short arc. For orbit determination using the Gauss method, the obtained azimuth and elevation angles are first converted into right ascension and declination, which are shown in Figure 3.

Figure 2. Schematic view of the geometry of orbit determination for a sample space debris.

Figure 3. Schematic view of the grabber satellite's position.
For this purpose, the unit vector of the sensor coordinate system, which is mounted on the viewer, is first obtained for transformation from sensor coordinate system to the right ascension and declination coordinate system as follows:
 $$\left[{\matrix{L_{hx} \cr L_{hy} \cr L_{hz}}} \right]=\left[{\matrix {-\cos {(AZ)}\cos {(El)} \cr \sin {(AZ)}\cos {(El)} \cr \sin {(El)}}} \right]$$
$$\left[{\matrix{L_{hx} \cr L_{hy} \cr L_{hz}}} \right]=\left[{\matrix {-\cos {(AZ)}\cos {(El)} \cr \sin {(AZ)}\cos {(El)} \cr \sin {(El)}}} \right]$$
where L h , AZ and EL are line of sight unit vectors between the space debris and grabber satellite, azimuth, and elevation angles, respectively. After calculating the line of sight unit vector, it is transformed to the right ascension and declination frame as noted below:
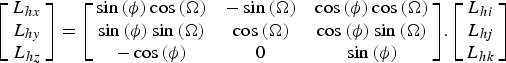 $$\left[{\matrix {L_{hx} \cr L_{hy} \cr L_{hz} \cr}} \right] =\left[{\matrix {\sin {(\phi )}\cos {({\Omega })} & -\sin {({\Omega })} & \cos {(\phi )}\cos {({\Omega })} \cr \sin {(\phi )}\sin {({\Omega })} & \cos {({\Omega })} & \cos {(\phi )}\sin {({\Omega })} \cr -\cos {(\phi )} & 0 & \sin {(\phi )}}} \right]\!. \left[{\matrix {L_{hi} \cr L_{hj} \cr L_{hk} \cr}} \right]$$
$$\left[{\matrix {L_{hx} \cr L_{hy} \cr L_{hz} \cr}} \right] =\left[{\matrix {\sin {(\phi )}\cos {({\Omega })} & -\sin {({\Omega })} & \cos {(\phi )}\cos {({\Omega })} \cr \sin {(\phi )}\sin {({\Omega })} & \cos {({\Omega })} & \cos {(\phi )}\sin {({\Omega })} \cr -\cos {(\phi )} & 0 & \sin {(\phi )}}} \right]\!. \left[{\matrix {L_{hi} \cr L_{hj} \cr L_{hk} \cr}} \right]$$
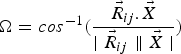 $$\Omega = cos^{-1}(\displaystyle{{\vec{R}_{ij}\kern-1pt{.}\,\vec{X}}\over{\mid\vec{R}_{ij} \parallel\vec{X}\mid}})$$
$$\Omega = cos^{-1}(\displaystyle{{\vec{R}_{ij}\kern-1pt{.}\,\vec{X}}\over{\mid\vec{R}_{ij} \parallel\vec{X}\mid}})$$
 $$\phi = cos^{-1}\left(\displaystyle{{\vec{R}_{ij}\kern-1pt{.}\,\vec{R}}\over{\mid\vec{R}_{ij} \parallel\vec{R}\mid}}\right)$$
$$\phi = cos^{-1}\left(\displaystyle{{\vec{R}_{ij}\kern-1pt{.}\,\vec{R}}\over{\mid\vec{R}_{ij} \parallel\vec{R}\mid}}\right)$$
where Ω, ϕ are right ascension and declination angles, respectively. Also
![]() $\vec{\hbox{X}}$
and
$\vec{\hbox{X}}$
and
![]() $\vec{\hbox{R}}$
are x-direction in the Earth-Centred-Inertial (ECI) frame and position vector of observer, respectively. There are numerical non-zero values including a, b and c which are capable of creating the following relationship:
$\vec{\hbox{R}}$
are x-direction in the Earth-Centred-Inertial (ECI) frame and position vector of observer, respectively. There are numerical non-zero values including a, b and c which are capable of creating the following relationship:
where
![]() $\vec{r}_{1}$
,
$\vec{r}_{1}$
,
![]() $\vec{r}_{2}$
and
$\vec{r}_{2}$
and
![]() $\vec{r}_{3}$
are position vector of space debris during the first, second and third observations. If the aforementioned relationship is solved in terms of
$\vec{r}_{3}$
are position vector of space debris during the first, second and third observations. If the aforementioned relationship is solved in terms of
![]() ${\vec{r}}_{2}$
, the following relationship will be created:
${\vec{r}}_{2}$
, the following relationship will be created:
For calculating the r 1 and r 3, the Lagrange coefficients, f and g are required through which the position vector for a specified time could be expressed in terms of position and velocity vectors during other times as noted below:
where
![]() $\vec{v}_{2}$
is the velocity vector of space debris during the second observation. Therefore,
$\vec{v}_{2}$
is the velocity vector of space debris during the second observation. Therefore,
![]() $\vec{r}_{1}$
and
$\vec{r}_{1}$
and
![]() $\vec{r}_{3}$
are calculated in terms of
$\vec{r}_{3}$
are calculated in terms of
![]() $\vec{r}_{2}$
. In addition, h
2 is angular momentum of space debris during the second observation and μ is the earth gravitational parameter. By combination the equations (Curtis, Reference Curtis2013), we have:
$\vec{r}_{2}$
. In addition, h
2 is angular momentum of space debris during the second observation and μ is the earth gravitational parameter. By combination the equations (Curtis, Reference Curtis2013), we have:
 $$\left[\matrix{L_{1x} & L_{2x} & L_{3x} \cr L_{1y} & L_{2y} & L_{3y} \cr L_{1z} & L_{2z} & L_{3z}} \right]\!.\left[\matrix{ c_{1}\rho_{1}\cr {c_{2}\rho }_{2}\cr c_{3}\rho_{3}} \right]=M=[L] \left[\matrix{ c_{1}\rho_{1}\cr {c_{2}\rho }_{2}\cr c_{3}\rho_{3}} \right]$$
$$\left[\matrix{L_{1x} & L_{2x} & L_{3x} \cr L_{1y} & L_{2y} & L_{3y} \cr L_{1z} & L_{2z} & L_{3z}} \right]\!.\left[\matrix{ c_{1}\rho_{1}\cr {c_{2}\rho }_{2}\cr c_{3}\rho_{3}} \right]=M=[L] \left[\matrix{ c_{1}\rho_{1}\cr {c_{2}\rho }_{2}\cr c_{3}\rho_{3}} \right]$$
where c
1 and c
3 are functions of
![]() $\vert \vec{r}_{2} \vert $
, t
1, t
2 and t
3. Moreover,
$\vert \vec{r}_{2} \vert $
, t
1, t
2 and t
3. Moreover,
![]() $\hat{L}$
1,
$\hat{L}$
1,
![]() $\hat{L}$
2 and
$\hat{L}$
2 and
![]() $\hat{L}$
3 are direction unit vectors between the debris and observer during the first, second and third observations. By inversing, the unit vectors of the line of sight matrix are:
$\hat{L}$
3 are direction unit vectors between the debris and observer during the first, second and third observations. By inversing, the unit vectors of the line of sight matrix are:
 $$\left[\matrix{c_{1}\rho_{1} \cr {c_{2}\rho }_{2} \cr c_{3}\rho_{3}}\right]=[L]^{-1}M$$
$$\left[\matrix{c_{1}\rho_{1} \cr {c_{2}\rho }_{2} \cr c_{3}\rho_{3}}\right]=[L]^{-1}M$$
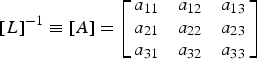 $$[L]^{-1}\equiv [A] =\left[\matrix{ a_{11} & a_{12} & a_{13} \cr a_{21} & a_{22} & a_{23} \cr a_{31} & a_{32} & a_{33}} \right]$$
$$[L]^{-1}\equiv [A] =\left[\matrix{ a_{11} & a_{12} & a_{13} \cr a_{21} & a_{22} & a_{23} \cr a_{31} & a_{32} & a_{33}} \right]$$
Afterwards, in terms of new variables the following relations are revealed:
 $$c_{1}\approx {\tau_{1} \over \tau_{2}}\left[ 1+{\lpar \tau_{2}^{2}-\tau_{1}^{2} \rpar \over {6}}h_{2} \right]=A_{1}+B_{1}h_{2}$$
$$c_{1}\approx {\tau_{1} \over \tau_{2}}\left[ 1+{\lpar \tau_{2}^{2}-\tau_{1}^{2} \rpar \over {6}}h_{2} \right]=A_{1}+B_{1}h_{2}$$
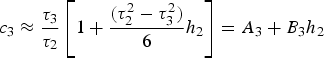 $$c_{3}\approx {\tau_{3}\over \tau_{2}}\left[ 1+{\lpar \tau_{2}^{2}-\tau_{3}^{2} \rpar \over {6}}h_{2} \right]=A_{3}+B_{3}h_{2}$$
$$c_{3}\approx {\tau_{3}\over \tau_{2}}\left[ 1+{\lpar \tau_{2}^{2}-\tau_{3}^{2} \rpar \over {6}}h_{2} \right]=A_{3}+B_{3}h_{2}$$
For obtaining ρ1, ρ2 and ρ3 the following relations are exploited:
Moreover, position vectors of the observer during three observations are expressed as noted below:
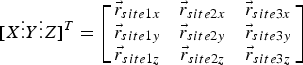 $$[X \vdots Y \vdots Z]^{T}=\left[ \matrix{ \vec{r}_{site1x} & \vec{r}_{site2x} & \vec{r}_{site3x}\cr \vec{r}_{site1y} & \vec{r}_{site2y} & \vec{r}_{site3y}\cr \vec{r}_{site1z} & \vec{r}_{site2z} & \vec{r}_{site3z}} \right]$$
$$[X \vdots Y \vdots Z]^{T}=\left[ \matrix{ \vec{r}_{site1x} & \vec{r}_{site2x} & \vec{r}_{site3x}\cr \vec{r}_{site1y} & \vec{r}_{site2y} & \vec{r}_{site3y}\cr \vec{r}_{site1z} & \vec{r}_{site2z} & \vec{r}_{site3z}} \right]$$
where
![]() $\vec{X}$
,
$\vec{X}$
,
![]() $\vec{Y}$
and
$\vec{Y}$
and
![]() $\vec{Z}$
are three directions in the ECI frame. Finally, for computation of the position vector of space debris during the second observation, the following equation is solved:
$\vec{Z}$
are three directions in the ECI frame. Finally, for computation of the position vector of space debris during the second observation, the following equation is solved:
By solving and obtaining eight possible answers, two cases occur. In the first case, if the space debris during the observation time lies in higher orbit relative to the satellite, that is
![]() $\vert \vec{r}_{2} \vert >\vert \vec{r}_{site2} \vert $
, the largest root is the desired solution. In the second case, if the satellite lies in higher orbit during the observation time relative to the space debris, that is
$\vert \vec{r}_{2} \vert >\vert \vec{r}_{site2} \vert $
, the largest root is the desired solution. In the second case, if the satellite lies in higher orbit during the observation time relative to the space debris, that is
![]() $\vert \vec{r}_{2} \vert <\vert \vec{r}_{site2} \vert $
, the second-largest root is the solution. Therefore, the position vector of the debris is eventually obtained as an input for the EKF for increasing the robustness and accuracy of the Gauss Method, which is described in detail in the next Section.
$\vert \vec{r}_{2} \vert <\vert \vec{r}_{site2} \vert $
, the second-largest root is the solution. Therefore, the position vector of the debris is eventually obtained as an input for the EKF for increasing the robustness and accuracy of the Gauss Method, which is described in detail in the next Section.
3. EKF AND ROBUST POSITIONING
In this work, the dynamics of the system are nonlinear. Hence, both the EKF and Unscented Kalman Filter (UKF) may be used. UKF is similar to the EKF but the linearization process is not applied in UKF. Because EKF is one of the most widely used filters for nonlinear systems, specifically because of its speed, this filter is employed in the current research (Giannitrapani et al., Reference Giannitrapani, Ceccarelli, Scortecci and Garulli2011). In fact, this filter converts the nonlinear system into a state-dependent time varying linear system; however, this transformation leads to some modelling errors. The significance of the Kalman filter is that all calculations for the system's state estimations (regardless of accuracies) are done using proper weighting. Relative motion between the earth and satellite is a two-body problem without any noise according to the law of universal gravitation.
3.1. Filtering and Estimation
Now, EKF is considered in detail. This filter is undoubtedly one of the most widely used filters for Gaussian nonlinear systems over the past few decades. By employing this filter, the system is first linearized through sampling times and then, systems' states are estimated for the next steps. Generally, the solving process for EKF is divided into two parts including predicting and updating times. During the estimation step, the measurement error covariance is first considered as follows (Wu et al., Reference Wu, Kong and Bo2013; Kaufman et al., Reference Kaufman, Lovell and Lee2016; Armellin et al., Reference Armellin, Lizia and Zanetti2016):
where plus and minus indices are germane to the next and previous times, respectively. State is estimated as noted below:
It should be noted that a fourth-order Runge-Kutta method has been utilised in this paper for calculating the
![]() $\hat{x}_{k}^{-}$
. Afterwards, the updating step is started by computation of the Kalman gain matrix as:
$\hat{x}_{k}^{-}$
. Afterwards, the updating step is started by computation of the Kalman gain matrix as:
where k k is the gain matrix. State variables and covariance matrices during the update process are calculated by means of observation data as follows:
3.2. Range Prediction Model
A diagramatic snapshot of orbits of observer space robot and space debris is shown in Figure 4. Here the state vector of the system is defined as (Wu et al., Reference Wu, Kong and Bo2013):

Figure 4. Supposed orbits of the grabber satellite and space debris.
Equations of motion in a Keplerian Orbit, comprising perturbations based on the law of universal gravitation are expressed as:
where μ is Earth gravitational parameter and
![]() ${\bi F}_{\bi p}$
model uncertainties due to the perturbations. Moreover, the motion state differential equation is defined as:
${\bi F}_{\bi p}$
model uncertainties due to the perturbations. Moreover, the motion state differential equation is defined as:
The second-order Taylor expansion for discrete form of the aforementioned relationship is:
where
![]() $O^{2}{}_{k}\lpar h \rpar $
is model uncertainty (Big-O-2) which is modelled as a Gaussian white noise with zero average and
$O^{2}{}_{k}\lpar h \rpar $
is model uncertainty (Big-O-2) which is modelled as a Gaussian white noise with zero average and
![]() $F\!\lpar X_{k} \rpar $
, Jacobian of F, is defined as below:
$F\!\lpar X_{k} \rpar $
, Jacobian of F, is defined as below:
State vectors of the satellite and space debris during k-th step are respectively calculated as follows:
Consequently, the Jacobian matrix of the state equation is derived as:
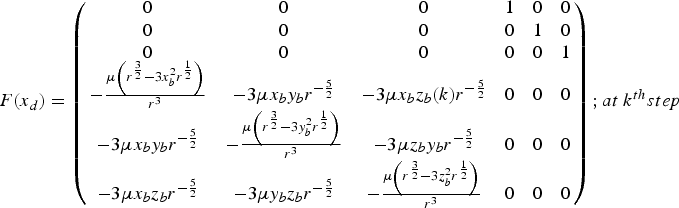 $${F(x}_{d})=\left( \matrix{ 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr -{\mu \left( r^{{3 \over 2}}-3x_{b}^{2}r^{{1 \over 2}} \right)\over r^{3}} & -3\mu x_{b}y_{b}r^{-{5\over 2}} & -3\mu x_{b}z_{b}\lpar k \rpar r^{-{5 \over 2}} & 0 & 0 & 0 \cr -3\mu x_{b}y_{b}r^{-{5 \over 2}} & -{\mu \left( r^{3\over 2}-3y_{b}^{2}r^{1\over 2} \right) \over r^{3}} & -3\mu z_{b}y_{b}r^{-{5 \over 2}} & 0 & 0 & 0 \cr -3\mu x_{b}z_{b}r^{-{5 \over 2}} & -3\mu y_{b}z_{b}r^{-{5 \over 2}} & -{\mu \left( r^{{3 \over 2}}-3z_{b}^{2}r^{1\over 2} \right)\over r^{3}} & 0 & 0 & 0} \right); at\ k^{th} step$$
$${F(x}_{d})=\left( \matrix{ 0 & 0 & 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 & 0 & 1 \cr -{\mu \left( r^{{3 \over 2}}-3x_{b}^{2}r^{{1 \over 2}} \right)\over r^{3}} & -3\mu x_{b}y_{b}r^{-{5\over 2}} & -3\mu x_{b}z_{b}\lpar k \rpar r^{-{5 \over 2}} & 0 & 0 & 0 \cr -3\mu x_{b}y_{b}r^{-{5 \over 2}} & -{\mu \left( r^{3\over 2}-3y_{b}^{2}r^{1\over 2} \right) \over r^{3}} & -3\mu z_{b}y_{b}r^{-{5 \over 2}} & 0 & 0 & 0 \cr -3\mu x_{b}z_{b}r^{-{5 \over 2}} & -3\mu y_{b}z_{b}r^{-{5 \over 2}} & -{\mu \left( r^{{3 \over 2}}-3z_{b}^{2}r^{1\over 2} \right)\over r^{3}} & 0 & 0 & 0} \right); at\ k^{th} step$$
where the exhibited elements are the resultant of the Jacobian operator on f. In addition, r denotes the squared range from the debris and is defined as noted below:
3.3. Bearing-Only Observation Model
In this work, measurement equation is considered as below:
where V resembles measurement noises. Moreover, the measured azimuth and elevation angles through mounted sensors on the observer robot are expressed as follows:
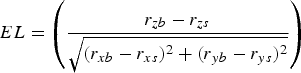 $$EL=\left({r_{zb}-r_{zs}\over\sqrt {\lpar r_{xb}-r_{xs} \rpar^{2}+\lpar r_{yb}-r_{ys} \rpar^{2}}}\right)$$
$$EL=\left({r_{zb}-r_{zs}\over\sqrt {\lpar r_{xb}-r_{xs} \rpar^{2}+\lpar r_{yb}-r_{ys} \rpar^{2}}}\right)$$
In the following, the Jacobian matrix of the measurement equation is derived as noted below:
 $$\eqalign{H &= \displaystyle{{\partial h} \over {\partial X_b}};at\;k^{th}\;step \cr & = \left[ {\matrix{{ - \displaystyle{{r_{y,bs}} \over {r_{x,bs}^2 + r_{y,bs}^2 }}} & {\displaystyle{{r_{x,bs}} \over {r_{x,bs}^2 + r_{y,bs}^2 }}} & 0 & 0 & 0 & 0 \cr { - \displaystyle{{r_{z,bs}r_{x,bs}} \over {{\left( {r_{x,bs}^2 + r_{y,bs}^2 } \right)}^{{\textstyle{1 \over 2}}}d^2}}} & { - \displaystyle{{r_{z,bs}r_{y,bs}} \over {{\left( {r_{x,bs}^2 + r_y^2 } \right)}^{{\textstyle{1 \over 2}}}d^2}}} & {\displaystyle{{{\left( {r_{x,bs}^2 + r_{y,bs}^2 } \right)}^{{\textstyle{1 \over 2}}}} \over {d^2}}} & 0 & 0 & 0}} \right]} $$
$$\eqalign{H &= \displaystyle{{\partial h} \over {\partial X_b}};at\;k^{th}\;step \cr & = \left[ {\matrix{{ - \displaystyle{{r_{y,bs}} \over {r_{x,bs}^2 + r_{y,bs}^2 }}} & {\displaystyle{{r_{x,bs}} \over {r_{x,bs}^2 + r_{y,bs}^2 }}} & 0 & 0 & 0 & 0 \cr { - \displaystyle{{r_{z,bs}r_{x,bs}} \over {{\left( {r_{x,bs}^2 + r_{y,bs}^2 } \right)}^{{\textstyle{1 \over 2}}}d^2}}} & { - \displaystyle{{r_{z,bs}r_{y,bs}} \over {{\left( {r_{x,bs}^2 + r_y^2 } \right)}^{{\textstyle{1 \over 2}}}d^2}}} & {\displaystyle{{{\left( {r_{x,bs}^2 + r_{y,bs}^2 } \right)}^{{\textstyle{1 \over 2}}}} \over {d^2}}} & 0 & 0 & 0}} \right]} $$
in which r x , r y , r z are elements of the range vector along x, y, and z directions while d is magnitude of the range vector at k th step:
4. SOLUTION OF LAMBERT PROBLEM AND ORBIT DEFINITION
The first stage in cleaning space debris from an orbit is determination of the debris' orbit through a space/ground observer. Since the position of the space debris is specified during a bearing-only process, the velocity vector should be calculated through some techniques for accomplishment of the requirements of orbit determination procedure. Since the Lambert approach (Curtis, Reference Curtis2013) is far more accurate than the Gibbs Method it is utilised in our preliminary orbit determination process. It is indicated that the Lambert Problem has a shorter computation time relative to the Gibbs one. In this method, orbital elements are calculated based on only two position observations and the time difference between them. It is supposed that the calculated position vectors during two different times are
![]() ${\bi r}_{\bf{1}}$
and
${\bi r}_{\bf{1}}$
and
![]() ${\bi r}_{\bf{2}}$
and the time difference between them is indicated. Afterwards, it is determined whether the orbit is retrograde or prograde. The angle between the two position vectors in the Lambert Problem is calculated as follows:
${\bi r}_{\bf{2}}$
and the time difference between them is indicated. Afterwards, it is determined whether the orbit is retrograde or prograde. The angle between the two position vectors in the Lambert Problem is calculated as follows:
Some auxiliary variables are employed for the sake of simplification, one of which is defined as:
Correspondingly, another auxiliary variable z is defined and obtained iteratively from numerical methods as follows:
The mentioned equation is a recursive one and the calculation process is continued until the value of z approaches its amount in the prior step. The auxiliary function of
![]() $y\lpar z \rpar $
is obtained from the following functions:
$y\lpar z \rpar $
is obtained from the following functions:
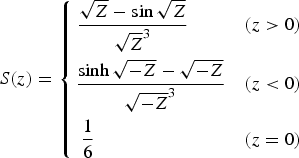 $$S(z)=\left\{\eqalign{{\sqrt Z -\sin \sqrt Z \over \sqrt Z^{3}} \quad \quad\quad (z>0)\cr {\sinh \sqrt {-Z} -\sqrt {-Z} \over \sqrt {-Z}^{3}} \quad (z< 0)\cr {1\over6}\quad\quad\quad\quad\quad\quad\quad\quad(z=0)}\right.$$
$$S(z)=\left\{\eqalign{{\sqrt Z -\sin \sqrt Z \over \sqrt Z^{3}} \quad \quad\quad (z>0)\cr {\sinh \sqrt {-Z} -\sqrt {-Z} \over \sqrt {-Z}^{3}} \quad (z< 0)\cr {1\over6}\quad\quad\quad\quad\quad\quad\quad\quad(z=0)}\right.$$
 $$C(z)= \left\{\eqalign{{1-\cos \sqrt Z \over \sqrt Z^{3}} \quad \quad\quad (z>0) \cr {\cosh \sqrt {-Z} -1 \over \sqrt {-Z}^{3}} \quad \quad (z< 0) \cr {1\over 2} \quad \quad\quad\quad\quad\quad\quad(z=0)}\right.$$
$$C(z)= \left\{\eqalign{{1-\cos \sqrt Z \over \sqrt Z^{3}} \quad \quad\quad (z>0) \cr {\cosh \sqrt {-Z} -1 \over \sqrt {-Z}^{3}} \quad \quad (z< 0) \cr {1\over 2} \quad \quad\quad\quad\quad\quad\quad(z=0)}\right.$$
where C(z) and
![]() $S\lpar z \rpar $
are called Stumpff functions, Afterwards, Lagrange coefficients and their derivatives are obtained as noted below:
$S\lpar z \rpar $
are called Stumpff functions, Afterwards, Lagrange coefficients and their derivatives are obtained as noted below:
Eventually, velocity vectors at the two observation times are calculated as follows:
As noted above, the six classical orbital elements are obtained from a union of the precomputed position and velocity vectors. It is mentioned that the Lambert Approach is far easier than the Gibbs Method. To elucidate further, the space object in the Gibbs Method is observed three times, whereas two observations as well as the time difference between them are sufficient in the Lambert Approach. Note that as per our experiments, the required solving time in the Gibbs Method is nearly five times greater than in the Lambert Problem. After computing the position and velocity vectors, angular momentum, inclination angle, the eccentricity vector is obtained as noted below:
Afterwards, right ascension, argument of perigee, and the true anomaly angle are also attained as follows:
where
![]() $\hat{K}$
is a unit vector along z. Moreover, perigee radius, apogee radius and semi-major axis are calculated from relations exhibited in Curtis (Reference Curtis2013).
$\hat{K}$
is a unit vector along z. Moreover, perigee radius, apogee radius and semi-major axis are calculated from relations exhibited in Curtis (Reference Curtis2013).
5. MODEL-BASED ORBIT PREDICTION AND MECHANISATION
Prediction of space debris' orbit, during the observations, is an essential task; due to the perturbations such as the earth anomalies like oblateness and bulge, atmospheric and geomagnetic forces and moments, solar and galactic winds and so on. Any geocentric orbit suffers from dynamical changes of orbital elements. This lack of symmetry means that the force of gravity on a revolving object is not focused along the centre of the earth. While the gravitational field of a plainly spherical sphere depends on the distance from its centre, oblateness causes a variation with latitude, which is called zonal variation, as well. The second zonal harmonic
![]() $\lpar {J}_{{2}}\rpar \comma \; $
is a dimensionless factor, which indicates the effects of oblateness on orbits. In the following, the gravitational specific force (per unit mass) in an oblate globe is given by:
$\lpar {J}_{{2}}\rpar \comma \; $
is a dimensionless factor, which indicates the effects of oblateness on orbits. In the following, the gravitational specific force (per unit mass) in an oblate globe is given by:
in which
![]() ${\bi F}_{\bi p}$
stands for the perturbing acceleration that is due to the earth spherical defects. This perturbing acceleration is comprised of the following noted components:
${\bi F}_{\bi p}$
stands for the perturbing acceleration that is due to the earth spherical defects. This perturbing acceleration is comprised of the following noted components:
where
![]() $\hat{\bi e}_{r}\comma \; \hat{\bi e}_{\bot }\comma \; \hat{h}$
are respectively, radial, transverse and perpendicular unit vectors attached to the satellite. Furthermore, p
r
, p
⊥and p
h
all depend on j
2 that are computed from the following relations:
$\hat{\bi e}_{r}\comma \; \hat{\bi e}_{\bot }\comma \; \hat{h}$
are respectively, radial, transverse and perpendicular unit vectors attached to the satellite. Furthermore, p
r
, p
⊥and p
h
all depend on j
2 that are computed from the following relations:
 $$p_{r} = -{\mu \over r^{2}}{3\over 2}J_{2}\left( {R\over r} \right)^{2}[{1-3}{sin}^{2}i\ {\sin}^{2}(\omega +\theta)]$$
$$p_{r} = -{\mu \over r^{2}}{3\over 2}J_{2}\left( {R\over r} \right)^{2}[{1-3}{sin}^{2}i\ {\sin}^{2}(\omega +\theta)]$$
 $$p_{\bot } = -{\mu \over r^{2}}{3\over 2}J_{2}\left( {R\over r} \right)^{2}{sin}^{2}i\ {\sin}[2(\omega +\theta)]$$
$$p_{\bot } = -{\mu \over r^{2}}{3\over 2}J_{2}\left( {R\over r} \right)^{2}{sin}^{2}i\ {\sin}[2(\omega +\theta)]$$
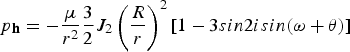 $$p_{\bf h} = -{\mu \over r^{{2}}}{{3}\over{2}}J_{{2}}\left( {R\over r} \right)^{{2}}{[1-3}{sin}{2}isin{(}\omega + \theta{)]}$$
$$p_{\bf h} = -{\mu \over r^{{2}}}{{3}\over{2}}J_{{2}}\left( {R\over r} \right)^{{2}}{[1-3}{sin}{2}isin{(}\omega + \theta{)]}$$
Prussing and Conway (Reference Prussing and Conway1993) showed how p r , p ⊥ and p h affect time rates of change for Right Ascension and Argument of Perigee, respectively.
Evidently, the time variation of the Right Ascension depends merely on the component of the instantaneous perturbing force, normal to the orbital plane, while the rate of change of the Argument of Perigee is subject to all the perturbation components.
5.1. Mechanisation in Inertial and Earth-Fixed Frames
To compute orbital position and velocity (
![]() $X\comma \; Y\comma \; Z\comma \; \dot{X}\comma \; \dot{Y}\comma \; \ \hbox{and}\ \dot{Z}$
) at time t, given,
$X\comma \; Y\comma \; Z\comma \; \dot{X}\comma \; \dot{Y}\comma \; \ \hbox{and}\ \dot{Z}$
) at time t, given,
![]() $a\comma \; e\comma \; i\comma \; \omega\comma \; \Omega\comma \; \ \hbox{and}\ T$
, at the first step the mean anomaly, MA, the eccentric anomaly, EA, and the true anomaly, ν, are computed respectively using the following relations (Chobotov, Reference Chobotov2002):
$a\comma \; e\comma \; i\comma \; \omega\comma \; \Omega\comma \; \ \hbox{and}\ T$
, at the first step the mean anomaly, MA, the eccentric anomaly, EA, and the true anomaly, ν, are computed respectively using the following relations (Chobotov, Reference Chobotov2002):
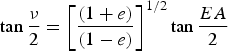 $$\tan{\nu \over 2} = \left[{(1+e)\over (1-e)}\right]^{1/2} \tan{EA \over 2}$$
$$\tan{\nu \over 2} = \left[{(1+e)\over (1-e)}\right]^{1/2} \tan{EA \over 2}$$
Afterwards, the radius, r, the specific angular momentum, h, the position and the velocity vectors' components, are computed as below:
To resolve coordinates in ECEF (Earth-Centred-Earth-Fixed) frame, the following relation is exploited:
 $$\left[{\matrix{X \cr Y \cr Z \cr}}\right]_{ECEF} = \left[{\matrix{{\cos \theta_G} & {\sin \theta_G} & 0 \cr {\sin \theta_G} & {\cos \theta_G} & 0 \cr 0 & 0 & 1 \cr } } \right]\left[{\matrix{{\dot X + \omega_EY} \cr {\dot Y + \omega_EX} \cr {\dot X} \cr}}\right]_{ECI}$$
$$\left[{\matrix{X \cr Y \cr Z \cr}}\right]_{ECEF} = \left[{\matrix{{\cos \theta_G} & {\sin \theta_G} & 0 \cr {\sin \theta_G} & {\cos \theta_G} & 0 \cr 0 & 0 & 1 \cr } } \right]\left[{\matrix{{\dot X + \omega_EY} \cr {\dot Y + \omega_EX} \cr {\dot X} \cr}}\right]_{ECI}$$
where θ G is the Greenwich sidereal time, and ω E is the Earth spin rate (7.2921158553x10−5 rad/sec). Furthermore, in order to reckon the space debris' ground track, which involves the geographic latitude and longitude, the following relations are utilised:
SIMULATION RESULTS
In the current work, we assume that the observer observes the debris' initial orbit from an unchanging orbit. This type of orbit is normally achieved via the Automatic Orbit Control System (AOCS) of the observer. The debris is also supposed to be the Switzerland CubeSat which encounters perturbations. Moreover, initial orbital elements for observer and space debris and orbital characteristics of the space debris obtained from the Lambert Method are presented in Table 1. By comparison with the reference data, it is clear that the employed hybrid procedure in this paper has sufficient accuracy during the preliminary orbit determination.
Table 1. Orbital elements of observer, space debris, and determined orbit.

The simulated orbits of the space debris and the observer robot are shown in Figure 5. In the next step, the variations of the space debris' position vector obtained using EKF are considered during the specified period. For observing the position vector variations, three different figures are considered based on the variations along x, y, and z. A view of simulated relative trajectory of space debris and the observer are shown in Figure 6, which demonstrates the complexity of the scenario. Moreover, the history of the reference orbit together with the estimated orbit by EKF are shown in Figure 6(b), where one might obtain a visual insight on the intimacy between them of the results.

Figure 5. A view of simulated orbits of space debris and the observer.

Figure 6. (a) A 3D/2D view of simulated relative trajectory of space debris and the observer. (b) History of the reference orbit and the estimated orbit by EKF.
The variations of the space debris' position vector along the x-axis are illustrated in Figure 7(a). As exposed, these variations due to different harmonies in the orbits of space debris and the observer are sinusoidal. Moreover, the distance between two peaks indicates the complete orbit cycle. The variations of the elements of space debris' position vector, along y-and-z-axes, are displayed in Figures 7(b), 7(c), respectively. Also, the variations of the space debris' velocity components, along x, y and z-axes, are exhibited in Figures 8(a), 8(b), and 8(c), in turn. The error components of the space debris' position vector are portrayed in Figures 9(a), 9(b), and 9(c), respectively. The error components of the space debris' velocity vector, along x, y and z-axes, are demonstrated in Figure 10(a), 10(b), and 10(c). As per the outcomes, error rates in the space debris' position and velocity vectors after the specified time increase a shallow slope because of the application of EKF. In other words, this issue demonstrates the efficacy of EKF, which is applied in this research. It is stated that these slight errors are created due to the uncertainties as well as produced errors because of the high simulation time. Note that after a specific time, errors will increase, and this issue indicates that it is necessary to utilise other auxiliary methods or integration of them for a precise orbit determination.

Figure 7. (a) Variations of the space debris' position vector along x-axis, (b) y-axis, and (c) z-axis.

Figure 8. (a) Variations of the space debris' velocity vector along x-axis, (b) y-axis, and (c) z-axis.

Figure 9. (a) Error variations of space debris' position vector along x-axis, (b) y-axis, and (c) z-axis.

Figure 10. (a) Error variations of space debris' velocity vector along x-axis, (b) y-axis, and (c) z-axis.
The determined orbital elements, including angular momentum, eccentricity, right ascension and inclination, true anomaly and argument of perigee are portrayed in Figures 11(a) to 11(b), respectively. The results of model-based prediction of space debris' orbit are demonstrated in Figures 12(a), 12(b), and 12(c). At the end, for better understanding of the orbital characteristics and the effects of perturbations, the ground track of the space debris and the observer are depicted in Figure 13. It is indicated that, due to considering a 98° for inclination angle and high sensitivity of the perturbations on it, the simulation scenario experiences the uppermost possible anomalies in the orbit of the space debris.

Figure 11. Estimated (a) Angular momentum, (b) Eccentricity (c) Right ascension, (d) Inclination, (e) True anomaly, and (f) Argument of perigee of the space debris' orbit.

Figure 12. Predicted time history of the space debris orbit, (a) 3D position (b) Right Ascension, (c) Angular Momentum, (d) Argument of Perigee, and (e) Eccentricity.

Figure 13. Ground track of space debris.
CONCLUSION
The main objective of this paper has been preliminary positioning, orbit determination, and model-based trajectory prediction of space debris, based on a robust procedure using iterative bearing-only in-orbit observations. In the first place, the problem was formulated with the purpose of calculating the distance vector between the space debris and an observer satellite. In addition, the assumption employed in this work was that the orbit of the observer was specified right from the beginning. Afterwards, the obtained position vector of the debris, by Gauss method, was corrected through EKF to diminish the errors. The Lambert Method was applied in this work for calculating the velocity vectors, and eventually, orbital elements of the space debris were obtained via acquired position and velocity vectors of the space debris. For future practical applications, a model-based method was exploited for prediction of the position and orbital characteristics of the debris. The efficacy and robustness of the presented method were demonstrated by running desired simulations over a practical mission. Particularly, it was verified that the suggested scheme was capable of producing a suitable solution for preliminary localisation and orbit determination of space debris based on the presented space-based observations, which was practical in preliminary rendezvous manoeuvres such as phasing and chasing exercises of any debris grabber space-machine.
















