3.1. The force model in the ONS

The ONS force model is established in the Target-Centred Inertial (TCI) coordinate system, taking Mars as a target:

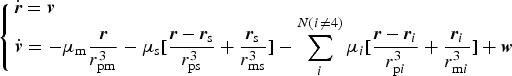(2)$$\left\{ {\matrix{ {\dot{\bi r} = {\bi v}} \hfill \cr {{\dot{\bi v}} = - \mu _{\rm m} \displaystyle{{\bi r} \over {r_{{\rm pm}}^3}} - \mu _{\rm s} [\displaystyle{{{\bi r} - {\bi r}_{\rm s}} \over {r_{{\rm ps}}^3}} + \displaystyle{{{\bi r}_{\rm s}} \over {r_{{\rm ms}}^3}} ] - \sum\limits_i^{N{\rm (}i \ne {\rm 4)}} {\mu _i [\displaystyle{{{\bi r} - {\bi r}_i} \over {r_{{\rm p}i}^3}} + \displaystyle{{{\bi r}_i} \over {r_{{\rm m}i}^3}} ] + {\bi w}}} \hfill \cr}} \right.$$

where in the TCI system r = [x, y, z]^T is the probe position vector, v = [v _x, v _y, v _z]^T is the probe velocity vector, μ _m, μ _s, μ _i are the gravitational parameters of Mars, Sun, and the ith planet respectively, r _ps, r _pm, r _pi are the distances between the probe and Sun, Mars, and the ith planet respectively, r_s = [x _s, y _s, z _s]^T are the coordinates of Sun, r_i = [x _i, y _i, z _i]^T are the position vector of the ith planet, which can be obtained from the ephemeris, and w = [w _x, w _y, w _z]^T are the process noises in the three-axis velocity.

The force model can be written in the general form:

(3)$${\dot {\bi X}}_1 (t) = f_1 ({\bi X}_1 (t),t) + {\bi w}_1 (t)$$

where X₁ = [x, y, z, v _x, v _y, v _z]^T is the ONS state vector, f ₁ (·) is the ONS dynamic model function , and w₁ = [w₁, w₂, w₃, w ₄, w ₅, w ₆]^T is the ONS process noise vector.

3.2. Measurement processing in the ONS

Although different types of measurements can be used in autonomous navigation (Paluszek et al., Reference Paluszek, Mueller and Littman2010), the angles between a target (Mars, Phobos, or Deimos) and its background stars from images captured by navigation sensor is used as measurement (Figure 2), because this kind of measurement can avoid the attitude determination errors.

Figure 2. Measurement of ONS.

The image of the target and background stars is the original data from the navigation sensor (Camera). Several steps are required to obtain the angle between the target and the known stars:

Step 1: Centroid identification. The pixel and line of the target (p, l) and those of the optical axis (p ₀, l ₀) can be calculated from the image by centroid-identification image processing technology.

Step 2: Coordinate Transformations

(1) Coordinates transformation from the pixel coordinate frame to the 2-Dimension (2D) image coordinate frame.

The pixel and line coordinates (p, l) (Figure 3) can be described in the 2D image frame as (x _2d, y _2d):

(4)$$\left[ {\matrix{ {x_{{\rm 2d}}} & {y_{{\rm 2d}}} \cr}} \right]^{\rm T} = {\bi K}^{ - 1} \left( {\left[ {\matrix{ p & l \cr}} \right]^{\rm T} - \left[ {\matrix{ {\,p_0} & {l_0} \cr}} \right]^{\rm T}} \right)$$

where K is the transformation matrix.

Figure 3. Coordinates definitions in navigation sensor.

(2) Coordinates transformation from the 2D image coordinate frame to the 3-Dimension (3D) sensor coordinate frame.

A unit vector (x _c, y _c, z _c) in the 3D sensor coordinate frame can be given as follows:

(5)$${\bi l}_{{\rm pc}}^{\rm c} = \left[ {\matrix{ {x_{\rm c}} & {y_{\rm c}} & {z_{\rm c}} \cr}} \right]^{\rm T} = \left[ {\matrix{ {x_{{\rm 2d}}} & {y_{{\rm 2d}}} & { - f} \cr}} \right]^{\rm T} /\sqrt {x_{{\rm 2d}}^2 + y_{{\rm 2d}}^2 + f^2} $$

where, f is the focal length, and ${\bi l}_{{\rm pc}}^{\rm c} $ is the unit vector from the celestial body (c) to the probe (p) with respect to the origin in the sensor coordinate frame.

Step 3: Angle calculation. The angle θ between the target vector and its background star vector can be calculated by

(6)$$\theta = \arccos \left[ {( - {\bi l}_{{\rm pc}}^{\rm c} ) \cdot ( - {\bi l}_{\rm s}^{\rm c} )} \right]$$

where ${\bi l}_{{\rm pc}}^{\rm c}, {\bi l}_{\rm s}^{\rm c} $ are the vectors from the target and the background star to the probe in the sensor coordinate frame derived from Step 2.

3.3. The measurement model in the ONS

The angles between Mars, Phobos and Deimos and their jth background star θ _mj, θ _pj, θ _dj can be expressed as

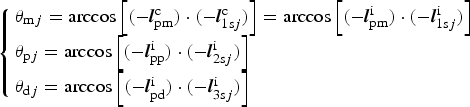(7)$$\left\{ {\matrix{ {\theta _{{\rm m}j} = \arccos \left[ {( - {\bi l}_{{\rm pm}}^{\rm c} ) \cdot ( - {\bi l}_{1{\rm s}j}^{\rm c} )} \right] = \arccos \left[ {( - {\bi l}_{{\rm pm}}^{\rm i} ) \cdot ( - {\bi l}_{1{\rm s}j}^{\rm i} )} \right]} \hfill \cr {\theta _{{\rm p}j} = \arccos \left[ {( - {\bi l}_{{\rm pp}}^{\rm i} ) \cdot ( - {\bi l}_{{\rm 2s}j}^{\rm i} )} \right]} \hfill \cr {\theta _{{\rm d}j} = \arccos \left[ {( - {\bi l}_{{\rm pd}}^{\rm i} ) \cdot ( - {\bi l}_{{\rm 3s}j}^{\rm i} )} \right]} \hfill \cr}} \right.$$

where in the sensor coordinate system, ${\bi l}_{{\rm pm}}^{\rm c} $ is the unit vector from Mars to the probe, ${\bi l}_{1{\rm s}j}^{\rm c} $ is the unit vector of the j th known star from the Mars image. In the TCI system, ${\bi l}_{{\rm pm}}^{\rm i}, {\bi l}_{{\rm pp}}^{\rm i}, {\bi l}_{{\rm pd}}^{\rm i} $ are the unit vectors to the probe from Mars, Phobos, and Deimos respectively, ${\bi l}_{1{\rm s}j}^{\rm i}, {\bi l}_{{\rm 2s}j}^{\rm i}, {\bi l}_{{\rm 3s}j}^{\rm i} $ are the unit vectors of the jth known star from the Mars image, Phobos image, and Deimos image, respectively.

Thus, the measurement model can be written in the general form:

(8)$${\bi Z}_{\rm 1} \left( t \right) = h_{\rm 1} \left( {{\bi X}_{\rm 1} \left( t \right),t} \right) + {\bi v}_{\rm 1} \left( t \right)$$

where Z₁ = [θ _m1, θ _m2, θ _m3, θ _p1, θ _p2, θ _p3, θ _d1, θ _d2, θ _d3]^T is the measurement vector, and ${\bi v}_{\rm 1} = [v_{\theta _{{\rm m1}}}, v_{\theta _{{\rm m2}}}, v_{\theta _{{\rm m3}}}, v_{\theta _{{\rm p1}}}, v_{\theta _{{\rm p2}}}, v_{\theta _{{\rm p3}}}, v_{\theta _{{\rm d1}}}, v_{\theta _{{\rm d2}}}, v_{\theta _{{\rm d3}}} ]^{\rm T} $ is the measurement noise vector, and $v_{\theta _{{\rm m1}}}, v_{\theta _{{\rm m2}}}, v_{\theta _{{\rm m3}}}, v_{\theta _{{\rm p1}}}, v_{\theta _{{\rm p2}}}, v_{\theta _{{\rm p3}}}, v_{\theta _{{\rm d1}}}, v_{\theta _{{\rm d2}}}, v_{\theta _{{\rm d3}}} $ are the measurement noise.

3.4. The initial state error of the ONS

The initial state error of the ONS is the position and velocity error in the TCI system at the initial moment, which is delivered from the navigation results in the HCI system at the end of the cruise phase.

Consequently, the target ephemeris error could be reflected as a part of the initial navigation error in the approach phase. Therefore the initial navigation error dX₁(0) can be divided into two parts as follows:

(9)$${\rm d}{\bi X}_{\rm 1} (0) = {\rm d}{\bi X}^{{\rm helio}} {\rm (0) + d}{\bi X}_{{\rm target}}^{{\rm helio}} (0)$$

where dX^helio(0) is the initial navigation error with respect to the Sun, ${\rm d}{\bi X}_{{\rm target}}^{{\rm helio}} (0)$ is the prior knowledge of the target ephemeris error at the initial moment.

4.1. The force model in the RNS

The RNS force model is established in the Helio-Centric Inertial (HCI) coordinate system:

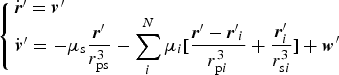(10)$$\left\{ {\matrix{ {{\dot{\bi r}^{\prime}} = {\bi v^{\prime}}} \hfill \cr {{\dot{\bi v}^{\prime}} = - \mu _{\rm s} \displaystyle{{{\bi r^{\prime}}} \over {r_{{\rm ps}}^3}} - \sum\limits_i^N {\mu _i [\displaystyle{{{\bi r^{\prime}} - {\bi r^{\prime}}_i} \over {r_{{\rm p}i}^3}} + \displaystyle{{{\bi r}_i ^{\prime}} \over {r_{{\rm s}i}^3}} ] + {\bi w^{\prime}}}} \hfill \cr}} \right.$$

where in the HCI system, r′ = [x′, y′, z′]^T is the probe position vector, v = [v′_x, v′_y, v′_z]^T is the probe velocity vector, r′_i = [x _i′, y _i′, z _i′]^T is the position vector of the ith planet, and w′ = [w′_x, w′_y, w′_z]^T are the process noises in the three-axis velocity.

The force model can be written in the general form:

(11)$${\dot {\bi X}}_2 (t) = f_2 ({\bi X}_2 (t),t) + {\bi w}_2 (t)$$

where X₂ = [x′, y′, z′, v′_x, v′_y, v′_z]^T is the RNS state vector, f ₂(·) is the RNS dynamic model function, and w₂ = [w′₁, w′₂, w′₃, w′₄, w′₅, w′₆]^T is the RNS process noise vector.

4.2. Measurements processing in the RNS

Range and range rate are two available measurements of the RNS. The range rate between a probe and a station $\dot R$ is measured by the signal frequency shift.

(12)$$\dot R = c[1 - {{\left( {\,f^{\prime}_{{\rm rec}} - \delta f_{atm} - \delta f_0} \right)} / {\,f_0}} ]$$

where c is the speed of light, f ₀ is the frequency of the signal from the station, f′_rec is the frequency of the signal received by the station, δf _atm, δf ₀ are the frequency errors caused by the atmospheric delay and the oscillator instability.

The range R between a probe and a station is measured by the signal delay time, and it can be expressed as

(13)$$R = c\tau + c\delta t_R - c\delta t_T + \delta \rho _{atm} {\rm +} \delta \rho _{{\rm trop}} {\rm +} \delta \rho _{{\rm ion}} {\rm +} \varepsilon $$

where τ is the signal transit time, δt _R is the receiver clock difference with true time, δt _T is the transmitter clock difference with true time, δρ _atm, δρ _ion are the atmospheric delay contribution and ionosphere contribution, δρ _trop is the troposphere delay, and ε represents remaining errors, such as the instrument noise (Vallado, Reference Vallado2007; Bar-Shalom et al., Reference Bar-Shalom, Rong and Kirubarajan2001).

4.3. The measurement model in the RNS

Ground stations can determine the probe position and velocity by measuring the ranges and range rates. A primary station with several secondary stations can accomplish the observing mission. The expressions of the range and range rate are given in the vector form by

(14)$$\left\{ \matrix{{\bi \rho} = (x^{\prime} - x_{\rm f} ){\bi u}_X + (y^{\prime} - y_{\rm f} ){\bi u}_Y + (z^{\prime} - z_{\rm f} ){\bi u}_Z \hfill \cr {\dot{\bi \rho}} = (v_x - v_{x_{\rm f}} ){\bi u}_X + (v_y - v_{y_{\rm f}} ){\bi u}_Y + (v_z - v_{z_{\rm f}} ){\bi u}_Z \hfill} \right.$$

where ρ is the probe position vector with respect to the ground station, ${\dot{\bi \rho}} $ is the relative probe velocity with respect to the ground station, $\rho, \dot \rho $ is the magnitude of ${\bi \rho}, {\dot{\bi \rho}} $, (x _f, y _f, z _f) are the coordinates of the ground station in the HCI system, and u_x, u_y, u_z are position unit vector of the probe with respect to the ground station.

Therefore, the measurement model can be written in the general form

(15)$${\bi Z}_2 (t) = h_2 ({\bi X}_2 (t),t) + {\bi v}_{\rm 2} (t)$$

where ${\bi Z}_{\rm 2} = [\rho _1, \dot \rho _1, \rho _2, \dot \rho _2, \rho _3, \dot \rho _3 ]^{\rm T} $ is the measurement vector of the RNS, ${\bi v}_{\rm 2} = [v_{\rho _1}, v_{\dot \rho _1}, v_{\rho _2}, v_{\dot \rho _2}, v_{\rho _3}, v_{\dot \rho _3} ]^{\rm T} $ is the measurement noise vector of the RNS, $\rho _1, \dot \rho _1, \rho _2, \dot \rho _2, \rho _3, \dot \rho _3 $ are the range and the range rate between the probe and the 1st, 2nd, and 3rd ground stations, and $v_{\rho _1}, v_{\dot \rho _1}, v_{\rho _2}, v_{\dot \rho _2}, v_{\rho _3}, v_{\dot \rho _3} $ is the measurement noise.

4.4. The initial state error of the RNS

The navigation results at the end of the cruise phase and the initial state error are both in the HCI system. Therefore, the initial navigation error dX₂(0) is equal to the navigation results at the end of the cruise phase

(16)$${\rm d}{\bi X}_{\rm 2} (0) = {\rm d}{\bi X}^{{\rm helio}} {\rm (0)}$$

5.1. Uncertainties of the gravity force of central body

When the probe enters into the gravitational sphere of influence of the target, the target is the central body. The acceleration from the central body is

(17)$${\bi a}_{{\rm cb}} = - \mu _{\rm t} {\bi r}/r^3 $$

where μ _t is the gravitational parameter of the target.

For a Mars probe in the approach phase (R _m < r ≤ 600000 km, R _m is the radius of the Mars), the acceleration from the central body is 1·1897 × 10⁻⁴ < a _cb ≤ 3·4962 m/s². Figure 4 gives the variation of the acceleration from the central body with the distance between the probe and Mars.

Figure 4. The central body gravitational acceleration of the Mars probe.

5.1.1. Uncertainty of the target ephemeris

The acceleration with respect to δ r, the changes in the target ephemeris, can be derived from the error propagation model of the target ephemeris (Ma et al., Reference Ma, Fang, Ning, Liu and Ge2015)

(18)$$\delta {\dot{\bi v}} = g^{\prime} ({\bi r})\delta {\bi r}$$

where $g({\bi r}) = - \mu _{\rm t} {{\bi r} / {r^3}} $, $\delta {\dot{\bi v}} = \delta {\ddot{\bi r}}$. It can be rewritten as follows:

(19)$$\delta {\ddot{\bi r}} = - \mu _{\rm t} \left[ {\displaystyle{{\delta {\bi r}} \over {r^3}} - 3\displaystyle{{{\bi r}\left( {{\bi r} \cdot \delta {\bi r}} \right)} \over {r^5}}} \right]$$

where $\delta {\ddot{\bi r}}$ is the acceleration with respect to the target ephemeris uncertainty, δ r is the target position error.

For a Mars probe in the approach phase, the ephemeris uncertainty of the central body (Mars) is less than 10 km, and the acceleration error caused by the Mars ephemeris uncertainty is about O(10⁻⁴).

5.1.2. Uncertainty of the target gravitational constant

The derivative of acceleration with respect to δμ _t, the change in the target gravitational parameter, can be derived from the error propagation model

(20)$$\delta {\ddot{\bi r}} = \left( {{\bi r}/r^3} \right)\delta \mu _{\rm t} $$

For a Mars probe in the approach phase, the gravitational parameter uncertainty of Mars is ± 0·1 km³/s², and the perturbation acceleration error caused by the Mars gravitational parameter uncertainty is about $O(10^{ - {\rm 5}} {\rm \sim}10^{ - {\rm 10}} {\rm )}$, which can be reasonably ignored due to the small magnitude.

5.2. Uncertainties of the perturbation of third body

Besides the gravities of the central body, other planets, and Sun, gravities from other celestial bodies, such as natural satellites and asteroids also act on the probe. The perturbation acceleration model is

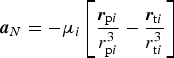(21)$${\bi a}_N = - \mu _i \left[ {\displaystyle{{{\bi r}_{{\rm p}i}} \over {r_{{\rm p}i}^3}} - \displaystyle{{{\bi r}_{{\rm t}i}} \over {r_{{\rm t}i}^{\rm 3}}}} \right]$$

where r_pi is the position vector from the third body to the probe, and r_ti is the position vector from the third body to the target.

For a Mars probe in the approach phase, r ≪ (r _ti, r _pi) and $r_{{\rm p}i} ^3 \approx r_{{\rm t}i} ^3 $, then the perturbation acceleration model can be simplified as follows

(22)$${\bi a}_N = - \mu _i {r / {r_{{\rm p}i}^3}} \left( {{{\bi r} / r}} \right)$$

Figure 5 gives the third body perturbation acceleration of all planets except Mars for a Mars probe in the approach phase, which indicates that the main third body perturbation acceleration is from the Sun, and the perturbation acceleration from the other bodies is less than 10⁻¹⁰ m/s². The third body perturbation acceleration from Phobos and Deimos is $10^{ - 1} {\sim}10^{ - 5} {\rm \;m\!/\!s}^2 $ at a low altitude, which cannot be ignored.

Figure 5. Third body gravitational perturbation acceleration.

5.3. Uncertainties of the gravity field of the target

As the target is not a perfectly spherical central body, the perturbing accelerations caused by a non-spherical central body will affect the force model accuracy. Taking Mars as an example, the aspherical-potential function U is modelled in spherical harmonics using the expression (Vallado, Reference Vallado2007; Lemonine et al., Reference Lemoine, Smith, Rowlands, Zuber, Neumann and Chinn2001)

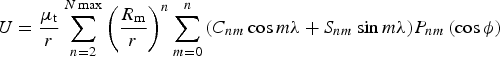(23)$$U = \displaystyle{{\mu _{\rm t}} \over r}\sum\limits_{n = 2}^{N\max} {\left( {\displaystyle{{R_{\rm m}} \over r}} \right)^n} \sum\limits_{m = 0}^n {\left( {C_{nm} \cos m\lambda + S_{nm} \sin m\lambda} \right)} P_{nm} \left( {\cos \phi} \right)$$

where, r, θ, λ are the body fixed coordinates, φ is latitude, and λ is longitude, C _nm and S _nm are the normalised coefficients of the spherical harmonic expansion, and P _nm are the normalised associated Legendre Functions.

Different Mars gravity field models are established by experimental data from interplanetary missions, such as GMM-2B, MGS75D, MGS95J, MRO110B, etc. The degree and order of the model determines the accuracy of the model. GMM-2B is an 80 × 80 spherical harmonics model calculated by Goddard Space Flight Center (GSFC), and MGS75D, MGS95J, MRO110B are 75 × 75, 95 × 95, 110 × 110 spherical harmonics models calculated by the Jet Propulsion Laboratory (JPL). Normalised gravitational coefficients of GMM-2B can be found in Lemonine (Reference Lemoine, Smith, Rowlands, Zuber, Neumann and Chinn2001).

Figure 6 gives the 4 × 4 nonsperical perturbation acceleration for a Mars probe in the approach phase. For a Mars probe in the approach phase, J ₂ ≈ O(10⁻⁴), J _2,2 ≈ O(10⁻⁴), $J_{{\rm 3,m}} \approx O{\rm (}10^{ - 10} ) \sim O{\rm (}10^{ - 6} {\rm )}$ and $J_{{\rm 4,m}} \approx O{\rm (}10^{ - 18} )\sim O{\rm (}10^{ - 9} {\rm )}$.

Figure 6. Mars 4 × 4 nonsperical perturbation acceleration.

5.4. Uncertainties of Solar radiation perturbation

When the probe is traveling in space, it is exposed to the Sun. Some incoming radiation from the Sun is absorbed, while some is reflected. The energy conversion leads to a force on the probe, which is the solar radiation pressure. Then the acceleration caused by solar radiation pressure can be modelled as

(24)$${{\bi a}_s} = - {c_R}{\,p_{SR}}({A / m}){{{{\bi r}_{{\rm sat}}}_ \odot } \big/ {\vert {{{\bi r}_{{\rm sat}}}_ \odot } \vert}} $$

where c _R is the reflectivity, its value depends on the composition and shape of the probe. If all the radiation is absorbed or reflected, then c _R = 1 or c _R = 2. If the object is translucent to incoming radiation, then c _R = 0. A is the incident area exposed to the Sun. p _SR is the force of solar pressure per unit area, and ${\bi r}_{{\rm sat} \odot} $ is the position vector from the probe to the Sun.

If the ratio of incident area to mass A/m = 0·02 m²/kg, and the average radiated power of solar radiation per unit area is 1·4 W/m², then the solar radiation pressure is p _SR = 4·65 × 10⁻⁶ N/m². For a Mars probe in the approach phase, the solar radiation perturbation acceleration is less than 10⁻⁷ m/s².

5.5. Uncertainties of atmosphere perturbation

Mars, Venus, Neptune and Titan are all surrounded by atmosphere. If the probe is operated at high speed in the atmosphere, the atmospheric drag will decrease the orbit altitude. The basic model is

(25)$${\bi a}_D = - C_D A_D \rho v^2 /2m\left( {{{\bi v} / v}} \right)$$

where C _D is the coefficient of drag, A _D is the exposed cross-sectional area, ρ is the atmospheric density, and v is the velocity of the probe relative to the atmosphere.

For Mars exploration, the available Mars atmosphere models include Mars GRAM 2010, Mars GRAM 2005, Mars GRAM 2000, etc. The atmospheric density depends on the altitude of the orbit. The atmospheric density and its drag effects decrease as the altitude rises. The atmospheric densities at 100 km and 50 km above the Mars surface are 7·5 × 10⁻⁹ kg/m³ and 5·6 × 10⁻¹¹ kg/m³, respectively.

If the altitude h = 150 km, the density is ρ = 5·6 × 10⁻¹¹ kg/m³, the coefficient of drag C _D is approximately 1, and the ratio of incident area to mass A _D/m = 0·02 m²/kg, then for a Mars probe in the approach phase, a_D < 1 × 10⁻⁵ m/s².

5.6. Total uncertainties of the force model

According to the analysis above, for a Mars probe in the approach phase, the uncertainties in the force models can be determined. The two main kinds of perturbation acceleration come from the gravity field of the target and target ephemeris uncertainty, and it is about 10⁻⁴ m/s². The other perturbation acceleration caused by solar radiation pressure, atmosphere drag and the target gravitational parameter can be reasonably ignored due to their small magnitude.

6.1. Filter methods for two navigation subsystems

Because of the nonlinear problem of the force models, a nonlinear filter should be used. Extended Kalman Filter (EKF) (Lee and Kyle, Reference Lee and Kyle2004), Unscented Kalman Filter (UKF) (Julier and Uhlmann, Reference Julier and Uhlmann1997; Julier et al., Reference Julier, Uhlmann and Durrant-Whyte2000), and Unscented Particle Filter (UPF) (van der Merwe et al., Reference van der Merwe, Doucet, de Freitas and Wan2000; Payne and Marrs, Reference Payne and Marrs2004) are three well-known nonlinear filters. EKF is based on the analytical Taylor series expansion of the nonlinear state and measurement models and the state approximations introduce large errors due to the neglected nonlinearities. UKF is a method capturing the mean and covariance of the state using the true nonlinear models and a set of sigma sample points with the unscented transformation. These two methods have the limitation that they do not apply to a general non-Gaussian distribution. The Particle Filter (PF) implements a recursive Bayesian filter by Monte Carlo simulations. The performance of the PF heavily depends on the choices of the importance sampling density and resampling scheme, and the number of samples decides the time consumed. However, due to the strict real time and accuracy requirement, the time consuming characteristics of PF and the inaccuracy of EKF, UKF is used in the INS (Ning et al., Reference Ning, Ma, Peng, Quan and Fang2012b).

6.2. Target ephemeris correction

6.2.1. The analytical method for target ephemeris correction

The target ephemeris uncertainty can be calculated from the geometry of the Sun, Earth, the actual target, the target in ephemeris and the probe (Figure 7).

Figure 7. Geometry of the Sun, Earth, the Actual Target, the Target in ephemeris and the Interplanetary probe.

From Figure 7, the target ephemeris uncertainty Z_err can be derived from

(26)$${\bi Z}_{{\rm err}} = {\bi X}_{{\rm target}}^{\rm a} - {\bi X}_{{\rm target}}^{\rm p} $$

where, ${\bi X}_{{\rm target}}^{\rm p} $ and ${\bi X}_{{\rm target}}^{\rm a} $ are the predicted and actual target position vector in the HCI system, ${\bi X}_{{\rm target}}^{\rm p} $ can be obtained from target ephemeris database, and ${\bi X}_{{\rm target}}^{\rm a} $ can be calculated by

(27)$${\bi X}_{{\rm target}}^{\rm a} {\rm = } {\bi X}_{{\rm target}}^{{\rm helio}} $$

where ${\bi X}_{{\rm target}}^{{\rm helio}} $ can be measured from the results of the RNS and the ONS, as Equation (1) shows. Therefore, the target ephemeris uncertainty Z_err can be calculated as follows:

(28)$${\bi Z}_{{\rm err}} = {\bi X}_{{\rm radio}}^{{\rm helio}} - {\bi X}_{{\rm optical}}^{{\rm target}} - {\bi X}_{{\rm target}}^{\rm p} $$

6.2.2. The estimation method for target ephemeris correction

The ephemeris uncertainty leads to a high uncertainty of the probe position. The exact orientation of orbit plane is more uncertain, whereas the period of the planet motion is relatively accurate. Thus the magnitude of the velocity typically has accurate prior knowledge. Based on those facts, the target ephemeris error is modelled as constant (Ma et al., Reference Ma, Fang, Ning, Liu and Ge2015; Wang et al, Reference Wang, Zheng, Sun and Li2013).

Figure 8 shows the flow chart of the target ephemeris correction, and the specific steps are given as follows:

Figure 8. Navigation system flow chart.

(1) The state model of target ephemeris error. Since the variation of the target ephemeris error is slow in each filter period, the dynamics of the target ephemeris error can be modelled as:

(29)$${\dot{\bi X}}{\rm err} = 0$$

where ${\dot{\bi X}}{\rm err =} \left[ {\matrix{ {\dot x_{{\rm err}}} & {\dot y_{{\rm err}}} & {\dot z_{{\rm err}}} \cr}} \right]^{\rm T} $, (x _err, y _err, z _err) are the coordinates of the target ephemeris errors in the HCI system.

The discrete state model of the target ephemeris error can be given as

(30)$${\bi X}_{{\rm err}} (k + 1) = F_{{\rm err}} ({\bi X}_{{\rm err}} \left( k \right),k) + {\bi w}_{{\rm err}} (k)$$

where the mapping F _err (·) represents the process models and F _err (X_err(k), k) = Φ_err,k+1,kX_err,k, Φ_err,k+1,k is the state transition matrix at step k, X_err(k) is the state vector at step k and w_err (k) is the process noise vector.

(2) Measurement and its model. The measurement vector of the target ephemeris error Z_err can be obtained from the estimation of the ONS and the RNS, ${\bi X}_{{\rm optical}}^{{\rm target}} $ and ${\bi X}_{{\rm radio}}^{{\rm helio}} $

(31)$${\bi Z}_{{\rm err}} = {\bi X}_{{\rm radio}}^{{\rm helio}} - {\bi X}_{{\rm optical}}^{{\rm target}} - {\tilde{\bi X}}_{{\rm target}}^{\rm e} $$

where ${\tilde{\bi X}}_{{\rm target}}^{\rm e} $ is the estimation of target ephemeris vector.

Accordingly, the discrete measurement model of the target ephemeris error can be expressed as follows:

(32)$${\bi Z}_{{\rm err}} (k) = h_3 ({\bi X}_{{\rm err}}, k) + {\bi v}_3 (k)$$

where Z_err (k) is the measurement vector of ephemeris error at step k, the mapping h ₃ (·) represents the measurement models function, and v₃ (k) is the measurement noise vector of ephemeris errors at the step k.

(3) KF. According to the linear characteristics of the state model and measurement models of the ephemeris error, KF is utilised to estimate the target ephemeris error ${\hat{\bi X}}_{{\rm err,} k} $ and its covariance matrix P_err,k.

(4) Correction. ${\hat{\bi X}}_{{\rm err,} k} $ and P_err,k are provided for the force models of both RNS and ONS to correct the target ephemeris error. After the correction, the accuracy of the orbit dynamics is enhanced.

1) Correction on the force model of the ONS. In the ONS, the coordinates of all the celestial bodies are in the TCI system. Therefore, the target ephemeris error has no effect on the coordinates of the origin of the TCI system, and the coordinates of the actual target are [0, 0, 0]^T. However, the coordinates of other planets contain the Mars ephemeris errors owing to the coordinates transformation.

The ith celestial body position coordinates in the TCI system ${\bi X}_i ^{{\rm target}} $ can be expressed as

(33)$${\bi X}_i ^{{\rm target}} = {\bi X}_i ^{{\rm helio}} - {\bi X}_{{\rm target}}^{{\rm helio}} - {\bi X}_{{\rm err}} $$

where ${\bi X}_i ^{{\rm helio}} $ is the position coordinates of the ith celestial body in the HCI system, ${\bi X}_{{\rm target}}^{{\rm helio}} $ is the actual target ephemeris in the HCI system, X_err is the target ephemeris error, and ${\tilde{\bi X}}_{{\rm target}}^{{\rm helio}} {\bi = X}_{{\rm target}}^{{\rm helio}} + {\bi X}_{{\rm err}} $. Therefore, the ephemerides of other planets (or the Sun) used in the force model are affected by the target ephemeris error X_err, and the estimated target ephemeris error is used to correct the ephemerides of other planets in the state model

(34)$${\bi X}_i ^{{\rm target}} = {\bi X}_i ^{{\rm helio}} - {\bi X}_{{\rm target}}^{{\rm helio}} - {\bi X}_{{\rm err}} {\rm +} {\hat{\bi X}}_{{\rm err}} = {\bi X}_i ^{{\rm helio}} - {\tilde{\bi X}}_{{\rm target}}^{{\rm helio}} {\rm +} {\hat{\bi X}}_{{\rm err}} $$

where, ${\hat{\bi X}}_{{\rm err}} $ is the estimated target ephemeris error.

2) Correction of the force model of the RNS. In the RNS, the coordinates of all the celestial bodies are in the HCI system. The target ephemeris error only affects the coordinates of the target, and the corrected target ephemeris is given by

(35)$${\hat{\bi X}}_{{\rm target}}^{{\rm helio}} = {\bi X}_{{\rm target}}^{} - {\bi X}_{{\rm err}} {\rm +} {\hat{\bi X}}_{{\rm err}} = {\tilde{\bi X}}_{{\rm target}}^{{\rm helio}} {\rm +} {\hat{\bi X}}_{{\rm err}} $$

where ${\hat{\bi X}}_{{\rm target}}^{{\rm helio}} $ is the corrected target ephemeris.

6.3. Information fusion algorithm

X₁(k), P₁(k) and X₂(k), P₂(k) are the estimated values and error covariance matrix of ONS and RNS respectively. However, X₁(k), P₁(k) are described in the TCI system, whereas X₂(k), P₂(k) are in the HCI system. To integrate the information in the same coordinate system, X₂(k), P₂(k) are transformed to X′₂(k), P′₂(k) in the TCI system (see 6.4. Coordinates Transformation). The global optimal estimation and its error covariance X_g and P_g in the TCI system in the master filter is obtained by the following equations (Ning and Fang, Reference Ning and Fang2008):

(36)$${\bi X}_g (k) = {\bi P}_g \left( k \right)\left[ {{\bi P}_1^{ - 1} \left( k \right){\bi X}_1 \left( k \right) + {\bi P^{\prime}}_2^{ - 1} \left( k \right){\bi X^{\prime}}_2 \left( k \right)} \right]$$

(37)$${\bi P}_g \left( k \right) = \left[ {{\bi P}_1^{ - 1} \left( k \right) + {\bi P^{\prime}}_2^{ - 1} \left( k \right)} \right]^{ - 1} $$

(38)$${\hat{\bi X}}_i (k) = {\bi X}_g (k)$$

(39)$${\bi P}_i (k) = \beta _i \cdot {\bi P}_g ^{ - {\rm 1}} (k)$$

(40)$$\beta _{\rm 1} {\rm +} \beta _{\rm 2} \,{\rm = 1}$$

where β _i is the fusion coefficient, which is inversely proportional to the trace of the error covariance.

The stability of UKF is not as good as EKF, so the feedback is only performed to state variables of the position and velocity. The information fusion algorithm directly provides the navigation results with respect to Mars. Those with respect to Earth can be derived by coordinate transformation using updated ephemeris.

6.4. Coordinates Transformations

6.4.1. Coordinates Transformation from the HCI to TCI system

To integrate the information in the same system, the navigation results of the RNS X₂(k), P₂(k) in the HCI system are transformed to X′₂(k), P′₂(k) in the TCI system. The translation between the two systems is

(41)$${\bi X}_{\rm 2}^{\prime} = {\bi X}_{\rm 2} {\bi + X}_{{\rm target}}^{{\rm helio}} + \delta {\bi X}_{{\rm target}}^{{\rm helio}} $$

and

(42)$${\bi P}_{\rm 2} ^{\prime} = {\bi P}_{\rm 2} {\bi + P}_{{\rm target}}^{{\rm helio}} $$

where $\delta {\bi X}_{{\rm target}}^{{\rm helio}} $ is the ephemeris error of ${\bi X}_{{\rm target}}^{{\rm helio}} $, ${\bi P}_{{\rm target}}^{{\rm helio}} $ is the target ephemeris covariance, ${\bi P}_{{\rm target}}^{{\rm helio}} = {\bi P}_{{\rm err}} $.

6.4.2. Coordinates Transformation from the TCI system to ECI

To simultaneously provide the position and velocity with respect to Earth and the target, the results of the INS in the TCI system need to transform these in the ECI system, which can be expressed as follows

(43)$${\bi X}_{\rm g}^{\prime} = {\bi X}_{\rm g} - {\bi X}_{{\rm target}}^{{\rm helio}} - \delta {\bi X}_{{\rm target}}^{{\rm helio}} {\rm +} {\bi X}_{{\rm earth}}^{{\rm helio}} {\rm +} \delta {\bi X}_{{\rm earth}}^{{\rm helio}} $$

and

(44)$${\bi P}_{\rm g} ^{\prime} = {\bi P}_{\rm g} {\bi + P}_{{\rm target}}^{{\rm helio}} $$

where, X′_g and P′_g is the estimation and its covariance of the INS in the ECI system, $\delta {\bi X}_{{\rm earth}}^{{\rm helio}} $ is the ephemeris error of ${\bi X}_{{\rm earth}}^{{\rm helio}} $ which can be neglected owing to the long-term observation of the Sun from Earth.

6.5. Criterion of final navigation results

6.5.1. Final navigation results with respect to the target

Besides the INS, ONS alone can also provide the navigation result with respect to the target. The final navigation estimation ${\bf X}_g^{{\rm target}} $ and its covariance ${\bi P}_g^{{\rm target}} $ with respect to the target is chosen by their covariance as follows:

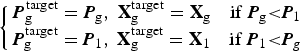(45)$$\left\{ {\matrix{ {{\bi P}_{\rm g}^{{\rm target}} = {\bi P}_{\rm g}, \; {\bf X}_{\rm g}^{{\rm target}} = {\bf X}_{\rm g} \quad {\rm if}\; {\bi P}_{\rm g} {\rm \lt} {\bi P}_1} \cr {{\bi P}_{\rm g}^{{\rm target}} = {\bi P}_1,\; {\bf X}_{\rm g}^{{\rm target}} = {\bf X}_1 \quad {\rm if}\; {\bi P}_1 {\rm \lt} {\bi P}_g} \cr}} \right.$$

6.5.2. Final navigation results with respect to Earth

Similarly, RNS alone can also provide the navigation result with respect to Earth. The final navigation estimation ${\bf X}_{\rm g}^{{\rm earth}} $ and its covariance ${\bi P}_{\rm g}^{{\rm earth}} $ with respect to Earth is chosen by their covariance as follows:

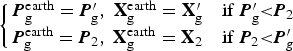(46)$$\left\{ {\matrix{ {{\bi P}_{\rm g}^{{\rm earth}} = {\bi P}_{\rm g} ^{\prime},\; {\bf X}_{\rm g}^{{\rm earth}} = {\bf X}_{\rm g} ^{\prime} \quad {\rm if}\; {\bi P}_{\rm g} ^{\prime} {\rm \lt} {\bi P}_2} \cr {{\bi P}_{\rm g}^{{\rm earth}} = {\bi P}_2 ,\; {\bf X}_{\rm g}^{{\rm earth}} = {\bf X}_2 \quad {\rm if}\; {\bi P}_2 {\rm \lt} {\bi P}_g ^{\prime}} \cr}} \right.$$

7.1. Simulation setup

The satellite Tool Kit Astrogator was used for creating the trajectory of the probe Earth-Mars transfers in 2013. The initial parameters were set as shown in Table 2.

Table 2. The initial parameters.

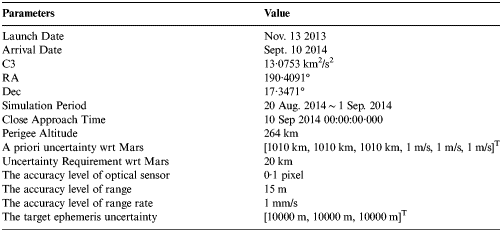
In the reference orbit model, the perturbation force included third body gravity from the Sun and other planets, spherical harmonic gravity of central body and solar radiation force. The spherical harmonic gravity of Mars was modelled as GMM2B (4 × 4) (Lemoine et al., Reference Lemoine, Smith, Rowlands, Zuber, Neumann and Chinn2001). Besides the gravitational perturbation from celestial bodies, solar radiation pressure was also included with the spherical solar radiation pressure model (Vallado, Reference Vallado2007). The reference orbit was generated by RKF89 numerical integrator using the fixed step (1 s).

The ephemerides of planetary bodies, the natural satellite and the star used JPL DE421 (Folkner, Reference Folkner2010), SPICE ephemeris (Acton, Reference Acton1996), and Tycho-2 star catalogue, respectively (Høg et al., Reference Høg, Fabricius, Makarov, Urban, Corbin, Wycoff, Bastian, Schwekendiek and Wicenec2000). The optical characteristics of Mars, Phobos, and Deimos sensors are shown in Table 3. Three deep space stations were located in Kashi, Qingdao and Santiago. The available arcs are given in Figure 9.

Figure 9. Available arcs of DSN station.

Table 3. Characteristics of the sensors.

7.2. Navigation results

Firstly, the results of the RNS and the ONS are given. Secondly, the impacts of the ephemeris uncertainty on information fusion are provided. Finally, the information fusion results using the analytical method and the estimation method for ephemeris correction are also given to show the importance of ephemeris correction and superior performance of the proposed method.

7.2.1. Navigation results of two navigation subsystems

Figure 10 and Table 4 give the navigation results (both with respect to Earth and Mars) of the RNS and ONS. As shown in Figure 10 and Table 4, the RNS can provide accurate navigation performance with respect to Earth, and the estimation accuracy of the position is 1·4993 m and that of the velocity is 7·9599 × 10⁻⁶ m/s, which is because RNS directly measures the observations with respect to Earth rather than Mars. However, for RNS alone, because of the inaccurate Mars ephemeris, the estimated position error with respect to Mars is inferior to that with respect to Earth. Therefore, the RNS usually offers navigation results with respect to Earth in interplanetary missions.

Figure 10. Performance comparisons of two navigation subsystems. (a) Position error (wrt Earth), (b) Velocity error (wrt Earth), (c) Position error (wrt Mars), (d) Velocity error (wrt Earth).

Table 4. Navigation results of two navigation subsystems.

Different from the RNS, the ONS provide accurate navigation performance with respect to Mars, that is 8·6747 × 10³ m in position and 0·0356 m/s. That is because ONS directly measures the observations with respect to Mars rather than Earth, and its navigation performance with respect to Mars does not depend on the Mars ephemeris, but on the accuracy of the measurements and models. When the Mars ephemeris uncertainty changes, the accuracy with respect to Mars provided by the ONS remains the same. However, also because of the inaccurate Mars ephemeris, the ONS cannot provide accurate navigation results with respect to Earth. Therefore, the ONS usually provides navigation results with respect to the target in interplanetary missions.

7.2.2. Fusion results with ephemeris uncertainty

Both the fusion results with and without ephemeris uncertainty and the fusion results with and without criteria are shown in Figure 11 and Table 5. It can be seen that the fusion accuracy is heavily influenced by the Mars ephemeris uncertainty. Because the Mars ephemeris uncertainty polluted the estimated position with respect to Mars in the RNS, the direct fusion results without criteria with respect to Earth are worse than the RNS.

Figure 11. Impacts of ephemeris error on information fusion results. (a) Position error (wrt Earth), (b) Velocity error (wrt Earth), (c) Position error (wrt Mars), (d) Velocity error (wrt Mars).

Table 5. Results of information fusion with ephemeris uncertainty.

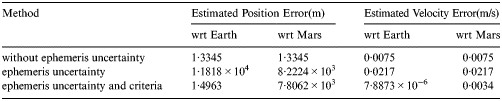
After using the criteria, compared with the subsystems alone, better accuracies with respect to Earth and Mars are achieved. This is because the criteria of final results integrate the more accurate results from each subsystem. However, compared with the result without ephemeris uncertainty, the accuracy has declined. Therefore, the Mars ephemeris uncertainty is still propagated into the INS, and its effects cannot be ignored.

7.2.3. Fusion results with ephemeris correction

Figure 12 and Table 6 compare the fusion results using three ephemeris correction methods, including no correction, the analytical method and the estimation method. The errors of the calculated and estimated ephemeris uncertainties from the analytical and estimation methods are given in Figure 13.

Figure 12. Information fusion results using estimation for ephemeris correction. (a) Position error (wrt Earth), (b) Velocity error (wrt Earth), (c) Position error (wrt Mars), (d) Velocity error (wrt Mars).

Figure 13. Estimation errors of ephemeris uncertainty.

Table 6. Performance comparison of information fusion using different methods for ephemeris correction.

By using the analytical method, the estimation errors with respect to both Earth and Mars decline a little. After the Mars ephemeris is calculated and corrected, the accuracy with respect to Mars is improved and is better than the ONS results. The calculated error of the Mars ephemeris uncertainty is within 7·8075 km (shown in Figure 13). Therefore, although the improvement is not evident, the improvement is attributed to the analytical method for the ephemeris correction, which provides the INS with a better ephemeris uncertainty result.

By using the estimation method, the INS can achieve the best accuracy. In particular, the estimation errors of the position with respect to Mars decline from 7·8062 km to 4·4704 km. The estimation error of the Mars ephemeris uncertainty is within 4·4707 km (Figure 13). The accuracy with respect to both Earth and Mars improved because of the corrected force models. It is indicated that the improvement of the Mars ephemeris uncertainty is attributable to the Mars ephemeris uncertainty model and KF helping to reduce the measurement noise from the analytical solution.

Therefore, the utilisation of the estimation method to correct ephemeris leads to the accuracy enhancement, which precisely estimates the ephemeris uncertainty, corrects the errors in the force models and reduces the effects of the Mars ephemeris uncertainty on the estimation accuracy. These results suggest that information fusion using estimation for ephemeris correction is an attractive solution for the ephemeris uncertainty problem.

7.3. Impact factors of estimation accuracy

The estimation accuracy of the ephemeris error is influenced by the parameters in the KF, such as the initial ephemeris error and covariance, the process noise covariance and the measurement noise covariance. The following are the specific effects of the impact factors on the estimation accuracy.

7.3.1. Initial ephemeris error and covariance

The initial ephemeris error X_err (0) is the prior knowledge of the ephemeris uncertainty at the initial moment, and the initial ephemeris covariance is P_err (0) = E(X_err (0)X_err (0)^T). The initial ephemeris error and covariance have some effects on the final estimation. Figure 14 and Table 7 give the estimation errors of the ephemeris uncertainty with different initial errors. From Figure 14 and Table 7, the estimation errors of ephemeris uncertainty increase with the initial ephemeris error growth.

Figure 14. Impacts of initial errors on the estimation error of the ephemeris uncertainty.

Table 7. Estimation accuracy with different initial errors.

7.3.2. Process noise covariance

The process noise covariance of the ephemeris uncertainty is defined as Q_err = E[(W_err)(W_err)^T]. However, the process noise covariance is presumed to be

$${\bi Q}_{{\rm err}} = q_0 \cdot {\rm diag}[1,1,1]$$

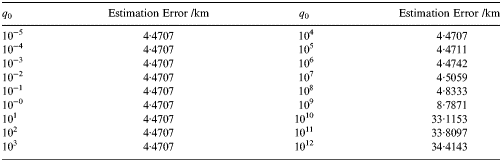
Figure 15 and Table 8 give the estimation errors of the ephemeris uncertainty with different process noise covariance matrices, and q ₀ varies from 10⁻⁵ to 10¹². From Figure 15 and Table 8, the estimation has the highest precision when q ₀ = 10². It is suggested that only if the Q_err matches the real process noise covariance, the estimation error is minimum. Therefore, the prior knowledge of the process noise covariance is required.

Figure 15. Impacts of the process noise covariance on the estimation error of the ephemeris uncertainty.

Table 8. Estimation accuracy with different process noise covariance matrices.

7.3.3. Measurement noise covariance

The measurement noise covariance of the ephemeris uncertainty is defined as R_err = E[(V_err)(V_err)^T]. In our case, the ideal one is equal to ${\tilde{\bi R}}_{{\rm err}} = {\bf E}\left[ {\left( {{\bi Z}_{{\rm err}} - {\tilde{\bi X}}_{{\rm err}}} \right)\left( {{\bi Z}_{{\rm err}} - {\tilde{\bi X}}_{{\rm err}}} \right)^{\rm T}} \right]$, ${\tilde{\bi X}}_{{\rm err}} $ is the real Mars ephemeris uncertainty. However, ${\tilde{\bi X}}_{{\rm err}} $ is not exactly known in practice. Because Mars ephemeris uncertainty is approximately constant, the estimation at the last step X_err (k − 1) can replace ${\tilde{\bi X}}_{{\rm err}} $. Therefore R_err (k) = E[(Z_err (k) − X_err (k − 1))(Z_err (k) − X_err (k − 1))^T] is used in simulations.

Figure 16 and Table 9 give the estimation errors of ephemeris uncertainty with different measurement noise covariance metrics. It is shown that the estimation is accurate when measurement noise covariance is the ideal one ${\tilde{\bi R}}_{{\rm err}} $. However because of the limited prior knowledge of the measurement noise, high estimation accuracy is hard to achieve.

Figure 16. Impacts of the measurement noise covariance on the estimation error of the ephemeris uncertainty.

Table 9. Estimation accuracy with different measurement noise covariance matrices.