1. INTRODUCTION
Comparing the coastline as seen from a ship with the corresponding image on a nautical navigational map is an action familiar to every navigator. The navigator visually searches the shoreline for features identified by their unique shape, locates such features on a map, and plots the ship's position relative to the feature. Further offshore, a radar image is also used in conjunction with a map. Distortions affecting radar images covering small areas are insignificant, and the images of the coastline provided by the map and the radar are quite similar.
Safety issues associated with this navigational approach are highlighted when the navigator must steer the ship from harbour to a named port on an unfamiliar coast. In such an instance, the navigator is responsible for the following actions:
• First, the navigator must plot the route on the map by analysing shapes and the location of the target port, taking note of the moles, entrance beacons, wharfs, embankments and port structures along the way.
• Second, during navigation, the navigator must determine the ship's position relative to coastline features identified on the map (Figure 1).
Figure 1. Left to right, images of coastline as seen from a ship with a perspective camera, the same coastline as seen on a navigational chart, and as seen by radar.
• Finally, during berthing manoeuvres at the end of the journey, the navigator must estimate the vessel's speed of approach and the position of the ship's hull relative to the edge of the port embankment (Figure 1).
The role of the navigator in this process can be duplicated by a mechanical system. Specifically, a system comprised of a specialised camera, a computer, digitized maps and processing algorithms can be developed that can compute a ship's position by comparing on board camera images of the coastline to the same features on a digitised map.
This paper summarises research evaluating the accuracy of using such a system to determine a ship's position by analysing the relationship of a spherical map to a visual image of the shoreline. The visual image is created with a Spherical Catadioptic Camera System (SCCS). The mapped image is generated by computer from an Electronic Navigational Chart (ENC) corresponding to the visual image of a dynamic spherical projection (Naus, Reference Naus2015).
This study grew out of the authors’ thesis work in the development of an automated comparative optical system intended to provide navigational data for ships manoeuvring near ports. Test methods described here reflect the authors’ prior experience in estimating a ship's position from radar images of the coast. (Wąż, Reference Wąż2010a; Reference Wąż2010b). The processes described here complement the work of other groups developing navigational systems based on processed imagery. The authors’ research group currently is researching automated imagery-based navigation system for vessels sailing along a track or a coastline (Hoshizaki et al., Reference Hoshizaki, Andrisani, Braun, Mulyana and Bethel2004; Snyder et al., Reference Snyder, Morris, Haley, Collins and Okerholm2004; Ryynanen et al., Reference Ryynanen, Vehkaoja, Osterberg and Joro2007).
The use of automated comparative optical systems to estimate the coordinates of a ship's position while manoeuvring in harbour areas has received little study until recently. Interest is growing now because of the recent growth in the use of imagery as a source of information on a ship's surroundings. Research has increased in the areas of nautical photogrammetry and robotics, disciplines at the intersection of mechanical technology, automated technology, electronic engineering, cybernetics and computer engineering. The following studies are particularly noteworthy in this sector:
• Active visual information analyses conducted by Robotic Research Group University (Knight, Reference Knight2002; Davison, Reference Davison2003) of Oxford University and of Texas (Stronger and Stone, Reference Stronger and Stone2007; Sridharan et al., Reference Sridharan, Kuhlmann and Stone2005);
• Automation of the process in the designation of external orientation elements, conducted within the OEEPE test (OEEPE, 1999; Jędryczka Reference Jędryczka1999);
• 3D model reconstruction use to localisation (Mouragnon, Reference Mouragnon2006; Yuanand and Medioni, Reference Yuanand and Medioni2006);
• Simultaneous Localisation and Mapping (SLAM) techniques conducted by Carneggie Mellon University Laboratory (Montemerlo, Reference Montemerlo2003; Stachniss et al., Reference Stachniss, Hanel and Burgared2004; Wang, Reference Wang2004); researches concerning the use of omnidirectional cameras (Xiaojin, Reference Xiaojin2008; Winters et al., Reference Winters, Gaspar, Grossmann and Santos-Victor2001; Benhimmane and Mailis, Reference Benhimmane and Mailis2006).
2. METHODS
The primary objectives of this study were to determine the geographical position coordinates of a ship using correlations between on board visual images, map images, and radar images. The visual images will be recorded with SCCS. The SCCS gear will be mounted high on the ship's hull. The map images will be computer-generated with ENC equipment. Only selected coastline features will be drawn using spherical dynamic projection (Naus, Reference Naus2015). Radar images will be obtained from the radar by means of a print screen saved in computer memory.
The procedure for mapping out coordinates will be implemented at regular time intervals in order to generate a collection of map images to be used for comparison with simultaneous visual images.
The visual geographical centre of map coordinates that maintains the largest probability to the visual image will be recognised as representing the best estimate of the coordinates of the ship's position. Both the visual and map images will be plotted to conform to the route of the ship as displayed on the ship's gyrocompass. The precision of the geographical coordinates for the ship's position will be evaluated by correlating shoreline images with constitutive coordinates over regular time intervals with a TOPCON Global Positioning System (GPS) receiver operating in the ASG-EUPOS system (mean error level of coordinates will not exceed 2 cm).
Adjusting the radar image to the map will only be performed for comparison purposes. Because of expected high resolution, the authors anticipated that a position obtained in this manner would be more precise than for low resolution radar images.
These assumptions are the basis for depicting geographical coordinates, choosing the most adequate experimental methods, and for deciding what instruments should be used. Because of the unique nature of this research, it was decided that the methods and equipment should be largely designed or modified by the authors.
The ship was equipped with an SCCS system for collecting data while manoeuvring in port. To process and analyse collected data, four program modules were designed:
• Electronic navigational chart generation on a spherical dynamic projection;
• A program to convert real images to edge images (for images registered by SCCS and obtained from the radar);
• A program to compare collections of real and map images;
• A program to evaluate precision in estimated ship positions with the shoreline to reference position correlation method (obtained from TOPCON GPS).
2.1. Data collection for research aboard ship
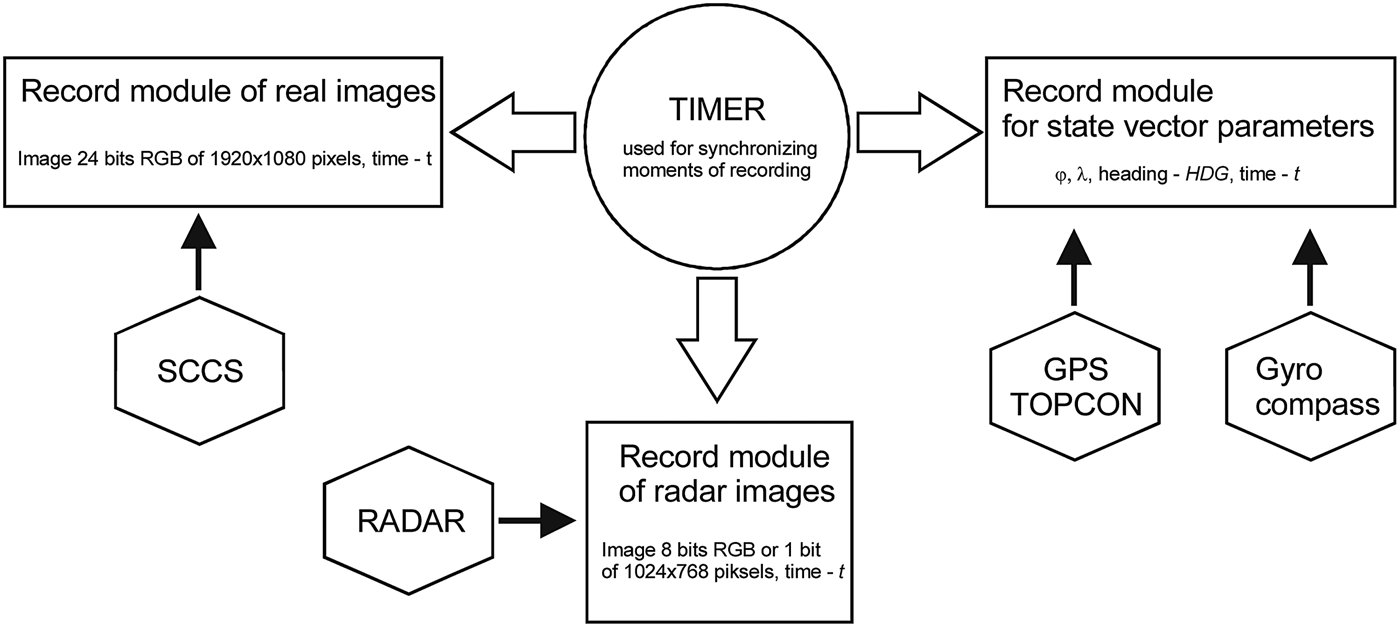
The Vessel Data Collection System included modules for recording real images as well as state vector parameters (Figure 2).

Figure 2. Schematic of shipboard data collection system.
The task for the system was to record synchronised images at regular time intervals from the SCCS (in real image recording module) and from the radar. An associated task was the recording of state vector parameters measured with navigational appliances (i.e. position coordinates SCCS-with a TOPCON GPS and course with Gyrocompass) in parameter recording modules.
The real image recording module was equipped with an SCCS prototype. The SCCS included the following four integrated system elements (Figure 3):
• A frame to mount camera and mirror as a single optical element;
• A 120 mm spherical mirror;
• A camera position regulator used to adjust the between the camera and the mirror (equalling 170 mm); and
• A CCD camera (Sony type HDR-CX130).

Figure 3. Spherical catadioptric camera system (a), and the measurement platform used during radar image registration (b).
The registration also required recording the entire raster radar image from the index. In addition to the conditional vector record made for each measurement session, the hydro-meteorological conditions of the basin were recorded. Thus, the radar had to be connected to both the oscilloscope and the computer. The connection required the use of a specialist PC RadarKit card capable of communicating between the computer and the radar. The computer and the oscilloscope were connected to a Bridge Master 250 radar (on the vessel ORP Arctowski). In order to be able to observe the video signals from the radar located on the computer screen, the following signals had to be connected to the computer: Video, Trigger, Bearing and Heading.
2.2. Generating map images
To safeguard the process of generating a set of map images (consisting of a visualised electronic navigational chart in a dynamic spherical projection) around an established ship position, a special software application was prepared. Its function was based on two program threads: the transformation of spatial objects in an ENC, and plotting and archiving map images.
The first function estimated ellipsoidal coordinates for all points representing the geographical location of spatial objects in ENC code (possessing geometrical representation and drawn on map images) for the transformation of ellipsoidal coordinates into ortho-Cartesian coordinates (IHO-3, 2002). The second function plotted archived map images that had been processed into ENC images of a spherical dynamic projection. Secondly, the function stored the images on a computer disc in Bitmap (BMP) format with a coded time index in their nominees.
Map images were based on mapping through a spherical surface on selected linear spatial objects level ENC (Figure 4)(Naus and Jankiewicz, Reference Naus and Jankiewicz2006a; Reference Naus and Jankiewicz2006b; Naus, Reference Naus2015).

Figure 4. Omnidirectional shoreline image as observed aboard ship SCCS and its correlate generated through dynamic spherical projection with ENC.
ENC spatial objects represented abutment points between water and land areas. Objects that were classified as such (IHO-1, 2000) included:
• shoreline construction (Acronym – SLCONS, Code – 122);
• land area (Acronym – LNDARE, Code – 71);
• floating docks (Acronym – FLODOC, Code – 57);
• hulks (Acronym – HULKES, Code – 65);
• pontoons (Acronym – PONTON, Code – 95); and
• pylon/bridge supports (Acronym – PYLONS, Code – 98).
Because these features facilities should be visible, they must have visually conspicuous attribute values (Acronym – CONVIS, Code – 83 equal “1”; this attribute is not coded by LNDARE).
To demarcate midpoints between lines representing selected spatial objects in ENC, a rasterisational algorithm of Bresenham's edge algorithm was used. This algorithm is one of the best both in terms of speed and in the projection of edges in rasterised form (Abrash, Reference Abrash1997).
2.3. Converting real images to edge images
The spherical catadioptric camera system used was a prototype, designed with nonprofessional tools and possessing components of average quality. Therefore it had flaws like any other prototype device. For the device in question, the largest flaws were associated with imperfections in the shape of the mirror's surface, as well as the positioning of the mirror and lens in relation to one another in the optical circuit, and the camera matrix CCD. These factors directly influenced geometrical errors of images based on the optical circuit.
The distorted optical imaging may, however, be corrected providing the radial distortion coefficient and tangential distortion coefficient of the camera's lens mirror is known and the affinity and nonorthogonality of the coordinate circuit on the CCD matrix can be determined.
As a result of the foregoing considerations, the hand-made SCCS was calibrated to achieve the following intrinsic parameters values (Websize_1, 2014; Websize_2, 2014): f i = 0.000067, f j = 0.000052, f s = 0.000006, c i = 2.345666, c j = 3.345789. These values were used in a matrix known as the camera matrix, ![]() ${{\bf M}_{{\bf IP}}}$, to correct the distorted location of every pixel,
${{\bf M}_{{\bf IP}}}$, to correct the distorted location of every pixel, ![]() ${\bf P} = {\left[ {i,\,j,\,1} \right]^{\rm T}}$ , of the recorded image
${\bf P} = {\left[ {i,\,j,\,1} \right]^{\rm T}}$ , of the recorded image ![]() ${\bf I}_{\bf 0}^{\bf R} $:
${\bf I}_{\bf 0}^{\bf R} $:
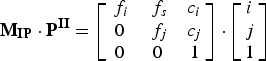 $${{\bf M}_{{\bf IP}}} \cdot {{\bf P}^{{\bf II}}} = \left[ {\matrix{ {{\,f_i}} & {{\,f_s}} & {{c_i}} \cr 0 & {{\,f_j}} & {{c_j}} \cr 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ i \cr j \cr 1 \cr}} \right]$$
$${{\bf M}_{{\bf IP}}} \cdot {{\bf P}^{{\bf II}}} = \left[ {\matrix{ {{\,f_i}} & {{\,f_s}} & {{c_i}} \cr 0 & {{\,f_j}} & {{c_j}} \cr 0 & 0 & 1 \cr}} \right] \cdot \left[ {\matrix{ i \cr j \cr 1 \cr}} \right]$$
thereby gaining image ![]() ${\bf I}_{\bf 1}^{\bf R} $ .
${\bf I}_{\bf 1}^{\bf R} $ .
![]() ${\bf I}_{\bf 0}^{\bf R} \;and\;{\bf I}_{\bf 1}^{\bf R} $ are digital images defined as a function in pixels space P to the colours space C,
${\bf I}_{\bf 0}^{\bf R} \;and\;{\bf I}_{\bf 1}^{\bf R} $ are digital images defined as a function in pixels space P to the colours space C, ![]() ${\bf I}:({\rm P}) \to ({\rm C})$, where (P) is a finite count of the pixels of a rectangular net described with an index collection IS(i 1, j 1;i 2, j 2) = {(i, j) ∈ R2:i 1 ≤ i ≤ i 2, j 1 ≤ j ≤ j 2} .
${\bf I}:({\rm P}) \to ({\rm C})$, where (P) is a finite count of the pixels of a rectangular net described with an index collection IS(i 1, j 1;i 2, j 2) = {(i, j) ∈ R2:i 1 ≤ i ≤ i 2, j 1 ≤ j ≤ j 2} .
The rules of the research required real shorelines to be compared to artificial shorelines. Therefore real images were subjected to edge detection in order to isolate edges representing abutment points between water and land, piers, floating docks and other structures encoded as spatial objects (possessing geometry) in ENC in the image. Canny's algorithm (Canny, Reference Canny1986) was used to perform edge detection because it can be used to calculate the following size-paired configuration parameters:
• The standard deviation, σ, white Gauss noise of the source image; and
• The High Threshold (HT) and Low Threshold (LT) of a hysteretic image contour result (to precisely localise the most important edges and represent them as one pixel line).
The parameters above allowed the transformation of real images, ![]() ${\bf I}_{\bf 1}^{\bf R} $, into images
${\bf I}_{\bf 1}^{\bf R} $, into images ![]() ${\bf I}_{\bf 2}^{\bf R} $,
${\bf I}_{\bf 2}^{\bf R} $, ![]() ${\bf I}_{\bf 3}^{\bf R} $,
${\bf I}_{\bf 3}^{\bf R} $, ![]() ${\bf I}_{\bf 4}^{\bf R} $ and finally into
${\bf I}_{\bf 4}^{\bf R} $ and finally into ![]() ${\bf I}_{\bf 5}^{\bf R} $. The process of transforming image
${\bf I}_{\bf 5}^{\bf R} $. The process of transforming image ![]() ${\bf I}_{\bf 1}^{\bf R} $ was achieved by iterations of the following actions:
${\bf I}_{\bf 1}^{\bf R} $ was achieved by iterations of the following actions:
2.3.1. Masking and converting image colours
Corrected image ![]() ${\bf I}_{\bf 1}^{\bf R} $, a 24-bit RBG, is first masked and then converted to
${\bf I}_{\bf 1}^{\bf R} $, a 24-bit RBG, is first masked and then converted to ![]() ${\bf I}_{\bf 2}^{\bf R} $, an 8-bit grey image consistent with (ITU, 2011) (Figure 5):
${\bf I}_{\bf 2}^{\bf R} $, an 8-bit grey image consistent with (ITU, 2011) (Figure 5):

Figure 5. Source image ![]() ${\bf I}_{\bf 1}^{\bf R} $ and
${\bf I}_{\bf 1}^{\bf R} $ and ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and conversion of colours.
${\bf I}_{\bf 2}^{\bf R} $ after masking and conversion of colours.
2.3.2. Removing noise from distorted images
This stage removes noise from source image ![]() ${\bf I}_{\bf 2}^{\bf R} $ by using an intermediary adaptation filter. The changed “blurred”
${\bf I}_{\bf 2}^{\bf R} $ by using an intermediary adaptation filter. The changed “blurred” ![]() ${\bf I}_{\bf 3}^{\bf R} $ was calculated with the following formula:
${\bf I}_{\bf 3}^{\bf R} $ was calculated with the following formula:
where σ 2 is the variance of noise in the entire image, σ 2(i, j) is the variance in pixel surrounding ![]() ${\bf I}_{\bf 2}^{\bf R} (i,j)$, and mean(i, j) is the average intensity in pixels surrounding
${\bf I}_{\bf 2}^{\bf R} (i,j)$, and mean(i, j) is the average intensity in pixels surrounding ![]() ${\bf I}_{\bf 2}^{\bf R} (i,j)$.
${\bf I}_{\bf 2}^{\bf R} (i,j)$.
For unilateral areas that remain undetailed (e.g. land or water areas), σ 2 = σ 2(i, j), and the image was only brought to ![]() ${\bf I}_{\bf 3}^{\bf R} (i,j) = mean(i,j)$. However, for detailed areas, σ 2 < σ 2(i, j), and the original images were not changed:
${\bf I}_{\bf 3}^{\bf R} (i,j) = mean(i,j)$. However, for detailed areas, σ 2 < σ 2(i, j), and the original images were not changed: ![]() ${\bf I}_{\bf 3}^{\bf R} (i,j) = {\bf I}_{\bf 2}^{\bf R} (i,j)$.
${\bf I}_{\bf 3}^{\bf R} (i,j) = {\bf I}_{\bf 2}^{\bf R} (i,j)$.
The use of an adaptation-levelling filter instead of the Gauss filter typically used in this method is the result of previous research conducted by the authors. This research evaluated the effectiveness of linear and nonlinear filtration methods in removing distortion from the surface of a sea image. The levelling adaptation filter proved to be the superior method.
2.3.3. Finding gradients
The cleared image (without noise) ![]() ${\bf I}_{\bf 3}^{\bf R} $ was then processed with a Sobel filter to produce the gradient facultative value. The gradient on a lateral level is
${\bf I}_{\bf 3}^{\bf R} $ was then processed with a Sobel filter to produce the gradient facultative value. The gradient on a lateral level is
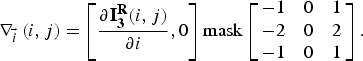 $${\nabla _{\vec i}}\left( {i,j} \right) = \left[ {\displaystyle{{\partial {\bf I}_{\bf 3}^{\bf R} (i,j)} \over {\partial i}},0} \right]{\rm mask}\left[ {\matrix{ { - 1} & 0 & 1 \cr { - 2} & 0 & 2 \cr { - 1} & 0 & 1 \cr}} \right].$$
$${\nabla _{\vec i}}\left( {i,j} \right) = \left[ {\displaystyle{{\partial {\bf I}_{\bf 3}^{\bf R} (i,j)} \over {\partial i}},0} \right]{\rm mask}\left[ {\matrix{ { - 1} & 0 & 1 \cr { - 2} & 0 & 2 \cr { - 1} & 0 & 1 \cr}} \right].$$The gradient on the horizontal level is:
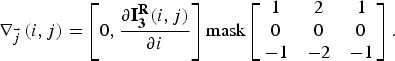 $${\nabla _{\vec j}}\left( {i,j} \right) = \left[ {0,\displaystyle{{\partial {\bf I}_{\bf 3}^{\bf R} (i,j)} \over {\partial i}}} \right]{\rm mask}\left[ {\matrix{ 1 & 2 & 1 \cr 0 & 0 & 0 \cr { - 1} & -2 & { - 1} \cr}} \right].$$
$${\nabla _{\vec j}}\left( {i,j} \right) = \left[ {0,\displaystyle{{\partial {\bf I}_{\bf 3}^{\bf R} (i,j)} \over {\partial i}}} \right]{\rm mask}\left[ {\matrix{ 1 & 2 & 1 \cr 0 & 0 & 0 \cr { - 1} & -2 & { - 1} \cr}} \right].$$
Based on the relationships above, values for every pixel ![]() ${\bf I}_{\bf 3}^{\bf R} (i,j)$ were found that satisfy the conditions below
${\bf I}_{\bf 3}^{\bf R} (i,j)$ were found that satisfy the conditions below
and also (rounded to: 0°, 90°, 45° or 135°)
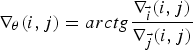 $${\nabla _\theta} (i,j) = arctg\displaystyle{{{\nabla _{\vec i}}(i,j)} \over {{\nabla _{\vec j}}(i,j)}}$$
$${\nabla _\theta} (i,j) = arctg\displaystyle{{{\nabla _{\vec i}}(i,j)} \over {{\nabla _{\vec j}}(i,j)}}$$
of incidental vector gradient. The calculation for the collection of gradients for image ![]() ${\bf I}_{\bf 3}^{\bf R} $ was used on concomitant levels of detection.
${\bf I}_{\bf 3}^{\bf R} $ was used on concomitant levels of detection.
2.3.4. Filtering pixels of non-maximum suppression
Image ![]() ${\bf I}_{\bf 3}^{\bf R} $ becomes distorted as distance increases from the real edge line and by thicknesses exceeding 1. This distortion was corrected by applying procedures to suppress non-maximal value pixels. The operation entails examining each pixel of the local maxima for consistency in their relationship to the edge. Neighbouring pixels on lines perpendicular to their gradients were also examined (
${\bf I}_{\bf 3}^{\bf R} $ becomes distorted as distance increases from the real edge line and by thicknesses exceeding 1. This distortion was corrected by applying procedures to suppress non-maximal value pixels. The operation entails examining each pixel of the local maxima for consistency in their relationship to the edge. Neighbouring pixels on lines perpendicular to their gradients were also examined (![]() ${\nabla _\theta} (i,j)$). Pixels with values different from their neighbours were eliminated, thereby producing image
${\nabla _\theta} (i,j)$). Pixels with values different from their neighbours were eliminated, thereby producing image ![]() ${\bf I}_{\bf 4}^{\bf R} $.
${\bf I}_{\bf 4}^{\bf R} $.
2.3.5. Hysteretic edging
The final stage consisted of hysteretic edging based on two previously determined verges: lower (posited at the value of 30), and upper (posited at the value of 60). The final choice of edge line pixels was based on these verges. This process entailed the analysis of the pixel gradient of the ![]() $\left\vert {\nabla (i,j)} \right\vert$ candidate in relation to established verges. If the gradients exceeded the posited upper value, the candidate pixel became a component of the edge; but if the value was less than the posited lower value, it was eliminated. Whenever a pixel was between the upper and lower values, it was accepted only if it was a component of a pixel row with a value above the hysteretic edge. The final edge image
$\left\vert {\nabla (i,j)} \right\vert$ candidate in relation to established verges. If the gradients exceeded the posited upper value, the candidate pixel became a component of the edge; but if the value was less than the posited lower value, it was eliminated. Whenever a pixel was between the upper and lower values, it was accepted only if it was a component of a pixel row with a value above the hysteretic edge. The final edge image ![]() ${\bf I}_{\bf 5}^{\bf R} $ was obtained in this manner (Figure 6).
${\bf I}_{\bf 5}^{\bf R} $ was obtained in this manner (Figure 6).

Figure 6. Image ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and conversion and
${\bf I}_{\bf 2}^{\bf R} $ after masking and conversion and ![]() ${\bf I}_{\bf 5}^{\bf R} $ after edge detection.
${\bf I}_{\bf 5}^{\bf R} $ after edge detection.
3. RESEARCH METHODS
Before beginning the research, a record was made of metrological data aboard the vessel ORP Arctowski on 25 October 2013.
The vessel manoeuvred around the XI naval port basin in Gdynia. It sailed round the wharf surrounding the basin, and then berthed on the wharf. Average speed of the vessel was 3·5 knots and the manoeuvre lasted 26 minutes. The vessel had covered a distance of about 16 cables (Figure 8).
Metrological data was recorded with a hand-made collecting system (see Section 2.1) in groups representing every second (Figure 7). Every data group contained recording time and one spherical real image including vector state parameters (position coordinates and course). The collection of all metrological data groups represented source material for our research, which focused on two primary issues:
1. Localizing vessel position in post-processing through comparing real images to map images generated about a previously determined position.
2. Determining the precision of every determined post-processing position through comparison with a referential position (determined by a TOPCOM GPS receiver at the exact same time as the real image).
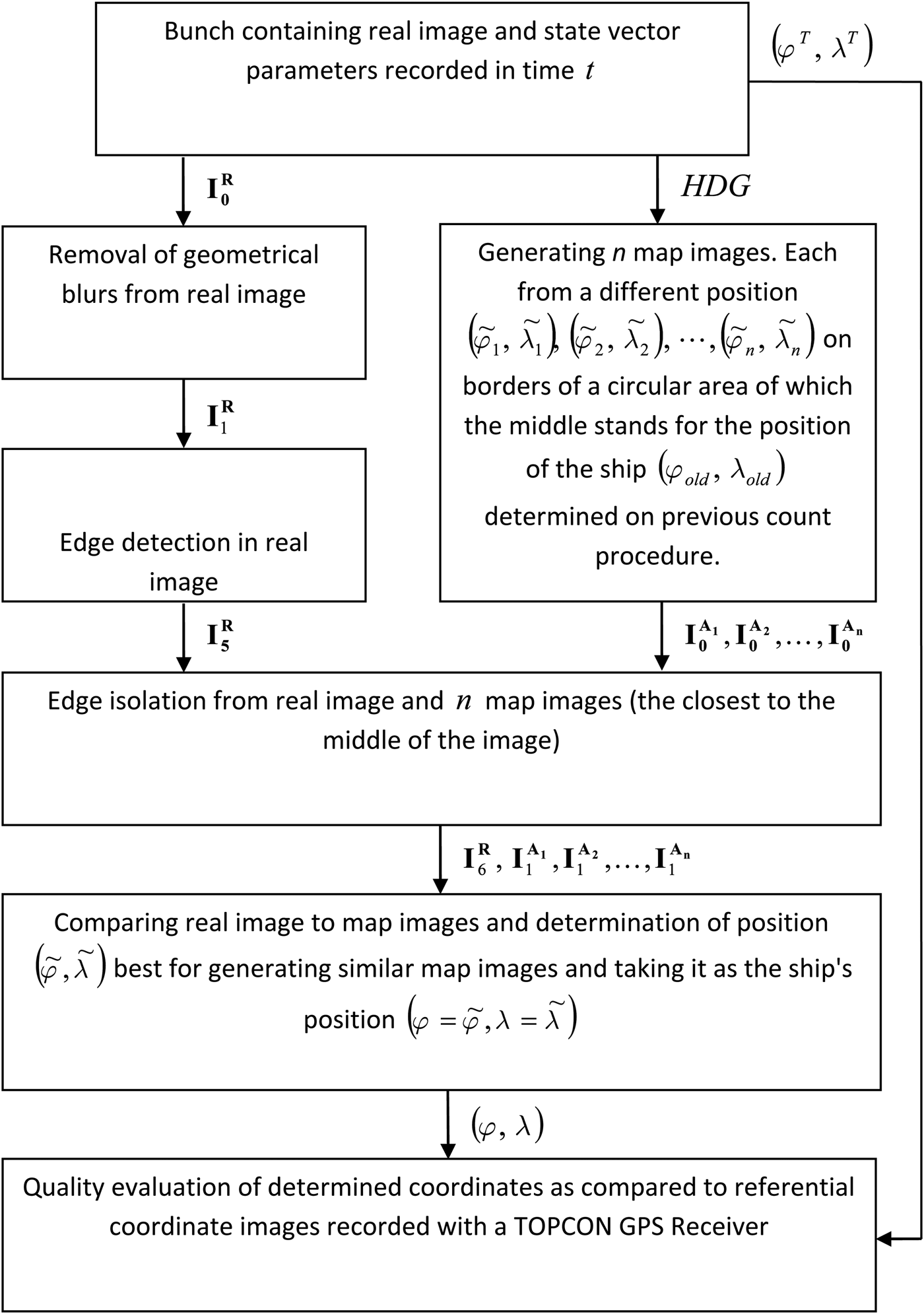
This work was conducted in accordance with the algorithm illustrated in Figure 9.

Figure 7. Location of the SCCS mounting on the ship.

Figure 8. The vessel manoeuvring route. (Map: https://maps.google.pl).

Figure 9. Research algorithm used.
As the research progressed, additional comparisons were conducted on each real image (or radar image) ![]() ${\bf I}_{\bf 6}^{\bf R} $ recorded at time t (after processing) with n map images
${\bf I}_{\bf 6}^{\bf R} $ recorded at time t (after processing) with n map images ![]() ${\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ (also after processing). Every map image was generated from a different position
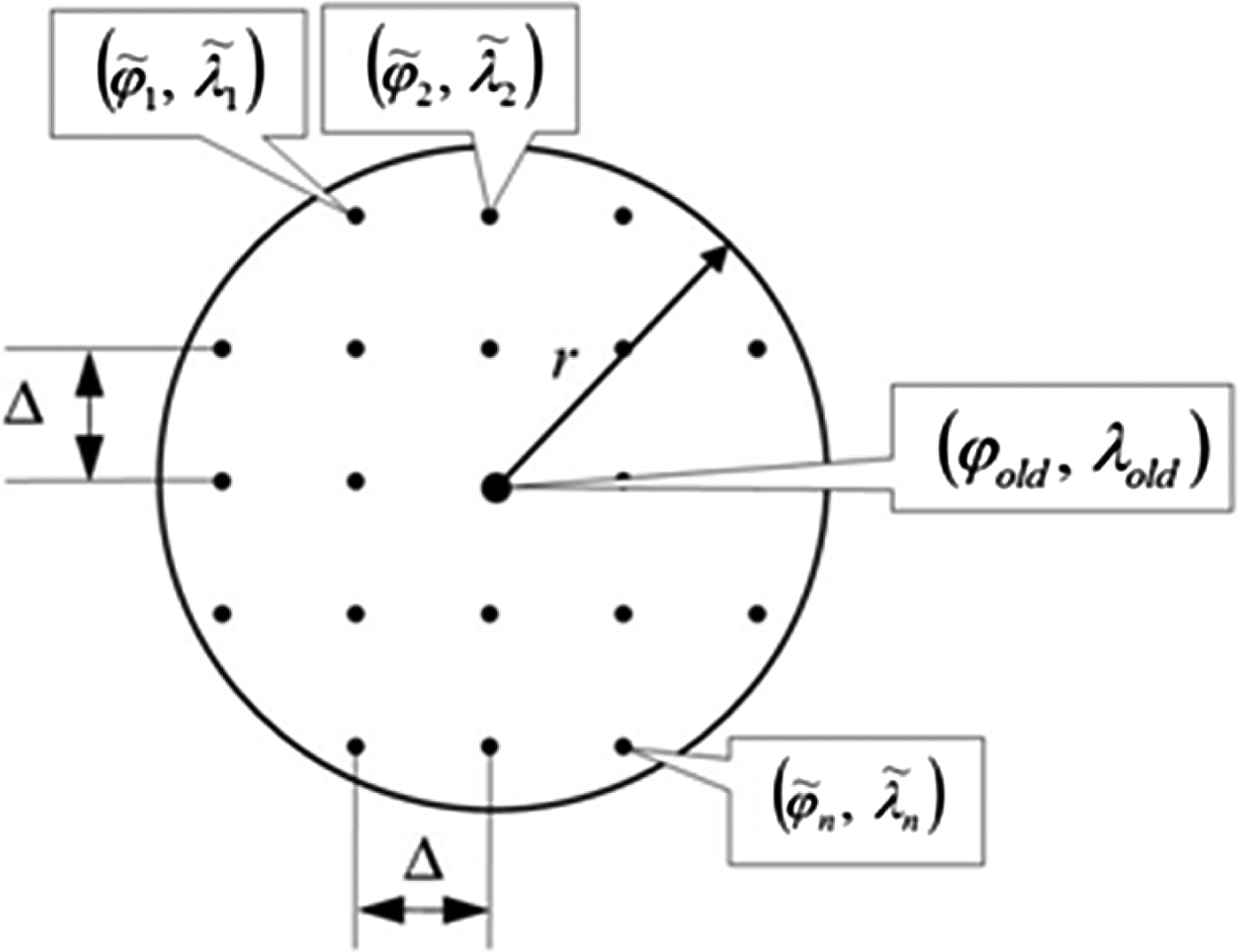
${\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ (also after processing). Every map image was generated from a different position ![]() $\left( {{{\tilde \varphi} _1},{{\tilde \lambda} _1}} \right),\left( {{{\tilde \varphi} _2},{{\tilde \lambda} _2}} \right), \cdots, \left( {{{\tilde \varphi} _n},{{\tilde \lambda} _n}} \right)$, along the borders of the circle of radius r (hereafter called the “search circle”) measured from the position of the ship (ϕ old, λ old) determined by previous estimates. All potential positions
$\left( {{{\tilde \varphi} _1},{{\tilde \lambda} _1}} \right),\left( {{{\tilde \varphi} _2},{{\tilde \lambda} _2}} \right), \cdots, \left( {{{\tilde \varphi} _n},{{\tilde \lambda} _n}} \right)$, along the borders of the circle of radius r (hereafter called the “search circle”) measured from the position of the ship (ϕ old, λ old) determined by previous estimates. All potential positions ![]() $\left( {{{\tilde \varphi} _1},{{\tilde \lambda} _1}} \right),\left( {{{\tilde \varphi} _2},{{\tilde \lambda} _2}} \right), \cdots, \left( {{{\tilde \varphi} _n},{{\tilde \lambda} _n}} \right)$ were distributed on a regular distance to the circle centre positioned in a permanent Δ (offset) from one another (measured horizontally and vertically) (Figure 10).
$\left( {{{\tilde \varphi} _1},{{\tilde \lambda} _1}} \right),\left( {{{\tilde \varphi} _2},{{\tilde \lambda} _2}} \right), \cdots, \left( {{{\tilde \varphi} _n},{{\tilde \lambda} _n}} \right)$ were distributed on a regular distance to the circle centre positioned in a permanent Δ (offset) from one another (measured horizontally and vertically) (Figure 10).

Figure 10. The position search circle.
Position ![]() $\left( {\tilde \varphi, \tilde \lambda} \right)$, which represents the closest correspondence between a map image and a real image was generated in time t and recognised as the new position of the ship
$\left( {\tilde \varphi, \tilde \lambda} \right)$, which represents the closest correspondence between a map image and a real image was generated in time t and recognised as the new position of the ship ![]() $\left( {\varphi = \tilde \varphi, \lambda = \tilde \lambda} \right)$. As a further step, n, another map image was generated to compare with another recorded real image. Before conducting the comparison, image
$\left( {\varphi = \tilde \varphi, \lambda = \tilde \lambda} \right)$. As a further step, n, another map image was generated to compare with another recorded real image. Before conducting the comparison, image ![]() ${\bf I}_{\bf 0}^{\bf R} $ was transformed into edge image
${\bf I}_{\bf 0}^{\bf R} $ was transformed into edge image ![]() ${\bf I}_{\bf 5}^{\bf R} $. Then the out-coming
${\bf I}_{\bf 5}^{\bf R} $. Then the out-coming ![]() ${\bf I}_{\bf 5}^{\bf R} $ image and the map image
${\bf I}_{\bf 5}^{\bf R} $ image and the map image ![]() ${\bf I}_{\bf 0}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 0}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 0}^{{{\bf A}_{\bf n}}} $ were transformed into images
${\bf I}_{\bf 0}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 0}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 0}^{{{\bf A}_{\bf n}}} $ were transformed into images ![]() ${\bf I}_{\bf 6}^{\bf R}, \;{\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ containing only edges localised closer to their centre (Figures 11 and 13). The last transformation concerned coordinate transformation (i, j) of the edge pixel of the images
${\bf I}_{\bf 6}^{\bf R}, \;{\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ containing only edges localised closer to their centre (Figures 11 and 13). The last transformation concerned coordinate transformation (i, j) of the edge pixel of the images ![]() ${\bf I}_{\bf 6}^{\bf R}, \;{\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ on the polar coordinates (α, d). The transformation was carried out in such a way that the polar coordinates (angle α and distances d) defined edge shapes in relation to the centre of the image (Figures 12 and 14).
${\bf I}_{\bf 6}^{\bf R}, \;{\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $ on the polar coordinates (α, d). The transformation was carried out in such a way that the polar coordinates (angle α and distances d) defined edge shapes in relation to the centre of the image (Figures 12 and 14).

Figure 11. Real images ![]() ${\bf I}_{\bf 5}^{\bf R} $ and
${\bf I}_{\bf 5}^{\bf R} $ and ![]() ${\bf I}_{\bf 6}^{\bf R} $.
${\bf I}_{\bf 6}^{\bf R} $.

Figure 12. Graph of distance d of edge ![]() ${\bf I}_{\bf 6}^{\bf R} $ in angle function α.
${\bf I}_{\bf 6}^{\bf R} $ in angle function α.

Figure 13. Map image ![]() ${\bf I}_{\bf 0}^{\bf A} $ and
${\bf I}_{\bf 0}^{\bf A} $ and ![]() ${\bf I}_{\bf 1}^{\bf A} $.
${\bf I}_{\bf 1}^{\bf A} $.

Figure 14. Graph of distance d of edge ![]() ${\bf I}_{\bf 1}^{\bf A} $ in angle function α.
${\bf I}_{\bf 1}^{\bf A} $ in angle function α.
The course of the test was analogical for radar images. The image obtained was then transformed into the contour form saved in the polar system. Literature refers to such an image as the “contour invariant” (Praczyk, Reference Praczyk2007).
The function describing the contour invariant d α is:
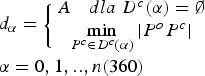 $$\eqalign{& {d_\alpha} = \left\{ {\matrix{ {A\quad dla\;{D^c}(\alpha ) = \emptyset} \cr {\mathop {\min} \limits_{{P^c} \in {D^c}(\alpha )} \left \vert {{P^o}{P^c}} \right \vert} \cr}} \right. \cr & \alpha = 0,1,..,n(360)} $$
$$\eqalign{& {d_\alpha} = \left\{ {\matrix{ {A\quad dla\;{D^c}(\alpha ) = \emptyset} \cr {\mathop {\min} \limits_{{P^c} \in {D^c}(\alpha )} \left \vert {{P^o}{P^c}} \right \vert} \cr}} \right. \cr & \alpha = 0,1,..,n(360)} $$where D c(α) is a set of visible image points (pixels) located on a specific bearing (α), thus representing radar echoes at a specific bearing; |P oP c| is the distance of the indicated pixel from midpoint of the image or the distance of the radar echo from the antenna; n is the extent of the applied resolution of the radar image invariant and A is a certain assumed distance larger than the observation scope.
By using the above dependency we entirely omit the process of edge detection. This is only possible for black and white radar images (1 bit).
Edge shapes described in this manner for real radar images were then compared for similarity to edge shapes of the map image. The first similarity measure applied was the minimal nonconformity factor metric (Borgefors, Reference Borgefors1986; Danielsson, Reference Danielsson1980):
Where ![]() ${d_{{\bf I}_1^{\bf A}}} (\alpha )$ is the distance to the edge in the direction of α on map image
${d_{{\bf I}_1^{\bf A}}} (\alpha )$ is the distance to the edge in the direction of α on map image ![]() ${\bf I}_{\bf 1}^{\bf A} $ and
${\bf I}_{\bf 1}^{\bf A} $ and ![]() ${d_{{\bf I}_6^{\bf R}}} (\alpha )$ is the distance to the edge in the direction of α on real image
${d_{{\bf I}_6^{\bf R}}} (\alpha )$ is the distance to the edge in the direction of α on real image ![]() ${\bf I}_{\bf 6}^{\bf R} $.
${\bf I}_{\bf 6}^{\bf R} $.
The second measure of similarity, the linear correlation factor, was applied to r k, and was calculated according to the following formula from Krysicki and Włodarski (Reference Krysicki and Włodarski1983):
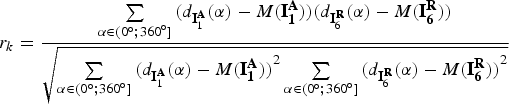 $${r_k} = \displaystyle{{\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {({d_{{\bf I}_1^{\bf A}}} (\alpha ) - M({\bf I}_{\bf 1}^{\bf A} ))({d_{{\bf I}_6^{\bf R}}} (\alpha ) - M({\bf I}_{\bf 6}^{\bf R} ))}} \over {\sqrt {\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {{{({d_{{\bf I}_1^{\bf A}}} (\alpha ) - M({\bf I}_{\bf 1}^{\bf A} ))}^2}\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {{{({d_{{\bf I}_6^{\bf R}}} (\alpha ) - M({\bf I}_{\bf 6}^{\bf R} ))}^2}}}}}}$$
$${r_k} = \displaystyle{{\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {({d_{{\bf I}_1^{\bf A}}} (\alpha ) - M({\bf I}_{\bf 1}^{\bf A} ))({d_{{\bf I}_6^{\bf R}}} (\alpha ) - M({\bf I}_{\bf 6}^{\bf R} ))}} \over {\sqrt {\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {{{({d_{{\bf I}_1^{\bf A}}} (\alpha ) - M({\bf I}_{\bf 1}^{\bf A} ))}^2}\sum\limits_{\alpha \in ({0^ \circ} ;{{360}^ \circ} ]} {{{({d_{{\bf I}_6^{\bf R}}} (\alpha ) - M({\bf I}_{\bf 6}^{\bf R} ))}^2}}}}}}$$ In Equation (10) we posited that ![]() $M({\bf I}_{\bf 7}^{\bf R} )$ is the distance arithmetic mean
$M({\bf I}_{\bf 7}^{\bf R} )$ is the distance arithmetic mean ![]() ${d_{{\bf I}_6^{\bf R}}} (\alpha )$ for
${d_{{\bf I}_6^{\bf R}}} (\alpha )$ for ![]() ${\bf I}_{\bf 6}^{\bf R} $, and
${\bf I}_{\bf 6}^{\bf R} $, and ![]() $M({\bf I}_{\bf 1}^{\bf A} )$ is the arithmetic mean
$M({\bf I}_{\bf 1}^{\bf A} )$ is the arithmetic mean ![]() ${d_{{\bf I}_1^{\bf A}}} (\alpha )$ for
${d_{{\bf I}_1^{\bf A}}} (\alpha )$ for ![]() ${\bf I}_{\bf 6}^{\bf R} $. Additionally Equations (9) and (10) were applied as distance input data
${\bf I}_{\bf 6}^{\bf R} $. Additionally Equations (9) and (10) were applied as distance input data ![]() ${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and
${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and ![]() ${d_{{\bf I}_1^A}} (\alpha )$ to the existing values for the
${d_{{\bf I}_1^A}} (\alpha )$ to the existing values for the ![]() ${\bf I}_{\bf 6}^{\bf R} $ edge. Of course, there might be situations when edges will not be isolated at all directions α. The coastline can be invisible at those directions. For angular intervals not maintaining continuity of edge in
${\bf I}_{\bf 6}^{\bf R} $ edge. Of course, there might be situations when edges will not be isolated at all directions α. The coastline can be invisible at those directions. For angular intervals not maintaining continuity of edge in ![]() ${\bf I}_{\bf 6}^{\bf R} $, distances
${\bf I}_{\bf 6}^{\bf R} $, distances ![]() ${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and
${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and ![]() ${d_{{\bf I}_1^A}} (\alpha )$ no posits were cited (Figure 16).
${d_{{\bf I}_1^A}} (\alpha )$ no posits were cited (Figure 16).
In the earlier efforts in adjusting radar images to a map, the ranges of inconsistencies of the contour image were entirely eliminated. These ranges illustrated that no radar echo was detected in the specified directions. These ranges were also not taken into account in the course of creating the invariant of the marine map.
For an edge appearing in all directions α ∈ (0°;360°), calculations were made for only one interval.
4. ANALYSIS OF RESULTS
Input data consisted of 1,560 groups of data recorded at time intervals of one second. Thus, in accordance with the algorithm of Figure 9, 1,560 positions were determined – (ϕ 1, λ 1), …, (ϕ 1560, λ 1560) (with an assumption that: r = 25 m, Δ = 0.1 m). These positions were examined for their accuracy by comparing them to referential positions ![]() $\left( {\varphi _1^T, \lambda _1^T} \right), \ldots, \left( {\varphi _{1560}^T, \lambda _{1560}^T} \right)$, determined by the use of a TOPCON GPS Receiver operated on the same time intervals (Figures 14 and 15). The following were applied as measures of assessment:
$\left( {\varphi _1^T, \lambda _1^T} \right), \ldots, \left( {\varphi _{1560}^T, \lambda _{1560}^T} \right)$, determined by the use of a TOPCON GPS Receiver operated on the same time intervals (Figures 14 and 15). The following were applied as measures of assessment:
• Distance of every estimated position (ϕ t, λ t) from the referential position
 $\varphi _t^T, \lambda _t^T $ at one second intervals t = 1, 2…1560,
$\varphi _t^T, \lambda _t^T $ at one second intervals t = 1, 2…1560,• Mean error of estimated position (ϕ t, λ t), calculated on the basis of all estimated positions (ϕ 1, λ 1), …, (ϕ 1560, λ 1560) in relation to all reference positions
 $\left( {\varphi _1^T, \lambda _1^T} \right), \ldots, \left( {\varphi _{1560}^T, \lambda _{1560}^T} \right)$.
$\left( {\varphi _1^T, \lambda _1^T} \right), \ldots, \left( {\varphi _{1560}^T, \lambda _{1560}^T} \right)$.
Results in comparing estimated positions to reference position with the minimal maladjustment factor r m are presented in a graphic form in Figure 17.

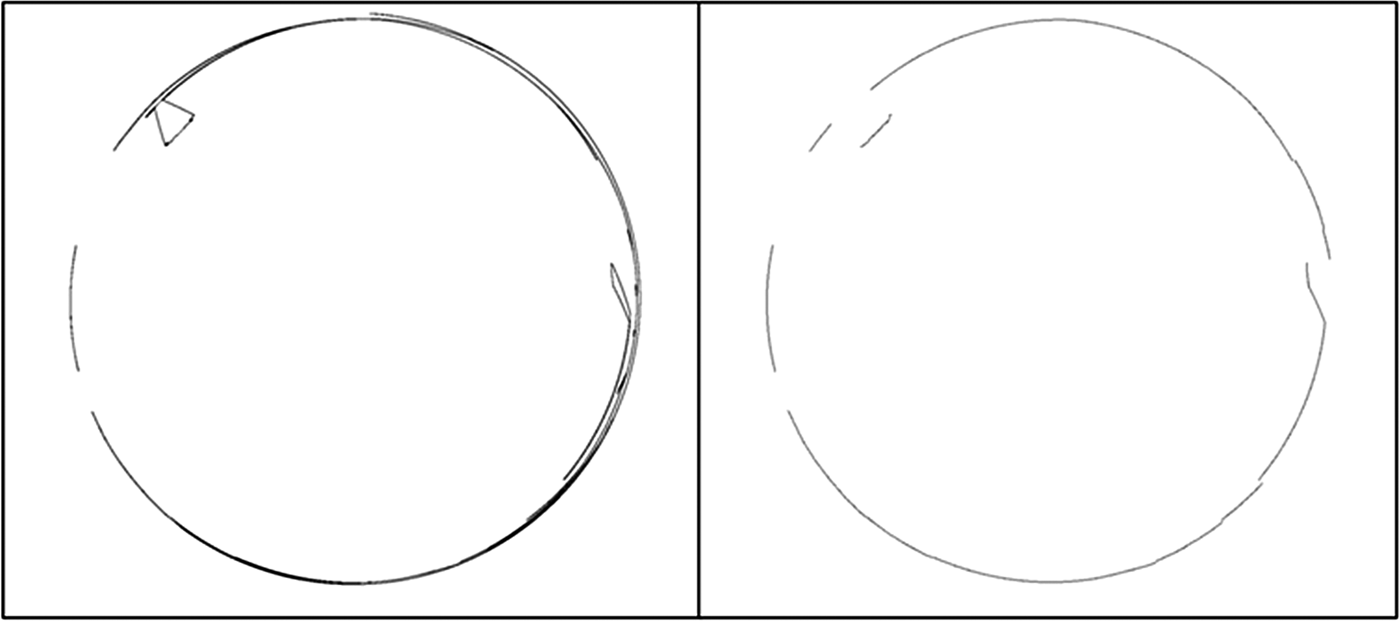
Figure 15. An example of a radar image and its contour invariant.

Figure 16. Graph of edge shapes ![]() ${\bf I}_{\bf 6}^{\bf R} $ with accepted angle count/computation intervals
${\bf I}_{\bf 6}^{\bf R} $ with accepted angle count/computation intervals ![]() ${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and
${d_{{\bf I}_6^{\bf R}}} (\alpha )$ and ![]() ${d_{{\bf I}_1^A}} (\alpha )$ for the real and radar image.
${d_{{\bf I}_1^A}} (\alpha )$ for the real and radar image.

Figure 17. Graphic representation of distance to the referential position ![]() $\left( {\varphi _t^T, \lambda _t^T} \right)$ from position (ϕ t, λ t) determined with application of r m in consecutive seconds t = 1, 2…1560.
$\left( {\varphi _t^T, \lambda _t^T} \right)$ from position (ϕ t, λ t) determined with application of r m in consecutive seconds t = 1, 2…1560.
Figure 18 shows a diagram of minimal value r m, for which the map image (chosen from n map images ![]() ${\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $, generated within the position search circle) is most similar to the real image
${\bf I}_{\bf 1}^{{{\bf A}_{\bf 1}}}, {\bf I}_{\bf 1}^{{{\bf A}_{\bf 2}}}, \ldots, {\bf I}_{\bf 1}^{{{\bf A}_{\bf n}}} $, generated within the position search circle) is most similar to the real image ![]() ${\bf I}_{\bf 6}^{\bf R}, $ as recorded by SCCS in every consecutive second t on board ship.
${\bf I}_{\bf 6}^{\bf R}, $ as recorded by SCCS in every consecutive second t on board ship.

Figure 18. Graphical representation of minimal maladjustment factor r m of the image ![]() ${\bf I}_{\bf 1}^{\bf A} $ which is most similar to image
${\bf I}_{\bf 1}^{\bf A} $ which is most similar to image ![]() ${\bf I}_{\bf 6}^{\bf R} $ over consecutive seconds t = 1,2…1560.
${\bf I}_{\bf 6}^{\bf R} $ over consecutive seconds t = 1,2…1560.
The mean error of the coordinate values of position (ϕ t, λ t), determined by the use of r m, totalled 5·72 m.
For radar images, such high precision of the selected position has not been achieved. After the digital processing and after removing unnecessary graphical information unrelated to radar imaging, the radar images were recorded at 640 × 640 pixels resolution. For a radar observation scope at 1·5 nautical miles, the distance between the centres of neighbouring pixels measured on the earth surface, referred to as GSD, was about 8·7 m. As a result of the tests on radar images, it has been determined that the value of the average position error was in the order of 3 pixels. This amounts to an error of about 26 m. As can be observed, this value exceeds the average error of the position based on the real image obtained from the SCCS by a factor of nearly five.
Analysing the graphs in Figures 17 and 18, one notices a dependency of the position precision on the minimal maladjustment value factor r m for images ![]() ${\bf I}_{\bf 1}^{\bf A} $ and
${\bf I}_{\bf 1}^{\bf A} $ and ![]() ${\bf I}_{\bf 6}^{\bf R} $. Figure 17 contains points for which position precision is distinctly greater, e.g., at time intervals where
${\bf I}_{\bf 6}^{\bf R} $. Figure 17 contains points for which position precision is distinctly greater, e.g., at time intervals where ![]() $t \in \left( {200\;{\rm s};300\;{\rm s}} \right) \wedge \left( {1200\;{\rm s;1300}\;{\rm s}} \right)$. Similarly, points exist for which precision falls markedly, such as during intervals where
$t \in \left( {200\;{\rm s};300\;{\rm s}} \right) \wedge \left( {1200\;{\rm s;1300}\;{\rm s}} \right)$. Similarly, points exist for which precision falls markedly, such as during intervals where ![]() $t \in \left( {700\;{\rm s};800\;{\rm s}} \right) \wedge \left( {1450\;{\rm s;1560}\;{\rm s}} \right)$. This is also confirmed by the graph in Figure 18 in which the r m value falls for the position with greater precision and increases for reference positions with little precision.
$t \in \left( {700\;{\rm s};800\;{\rm s}} \right) \wedge \left( {1450\;{\rm s;1560}\;{\rm s}} \right)$. This is also confirmed by the graph in Figure 18 in which the r m value falls for the position with greater precision and increases for reference positions with little precision.
In Figures 19 and 20, two preferable pairs of images are shown consisting of a real image and a map image most similar to it. Real images were recorded at time intervals of t = 250 s and t = 1250 s, which were times during which position accuracy was relatively high.

Figure 19. Real image ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and
${\bf I}_{\bf 2}^{\bf R} $ after masking and ![]() ${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best correlated map image
${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best correlated map image ![]() ${\bf I}_{\bf 1}^{\bf A} $ at time t = 250s.
${\bf I}_{\bf 1}^{\bf A} $ at time t = 250s.

Figure 20. Real Image ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and
${\bf I}_{\bf 2}^{\bf R} $ after masking and ![]() ${\bf I}_{\bf 6}^{\bf R} $ at the end converted, also the best correlated map image
${\bf I}_{\bf 6}^{\bf R} $ at the end converted, also the best correlated map image ![]() ${\bf I}_{\bf 1}^{\bf A} $ at time t = 1250s.
${\bf I}_{\bf 1}^{\bf A} $ at time t = 1250s.
Figures 19 and 20 clearly show that the shoreline in images ![]() ${\bf I}_{\bf 6}^{\bf R} $ and
${\bf I}_{\bf 6}^{\bf R} $ and ![]() ${\bf I}_{\bf 1}^{\bf A} $ possesses an irregular shape, and that image
${\bf I}_{\bf 1}^{\bf A} $ possesses an irregular shape, and that image ![]() ${\bf I}_{\bf 6}^{\bf R} $ does not possess any distortion whatsoever. The irregular shape is as a result of the ship manoeuvring past a port area that encroaches into the water area. The slight distortion of
${\bf I}_{\bf 6}^{\bf R} $ does not possess any distortion whatsoever. The irregular shape is as a result of the ship manoeuvring past a port area that encroaches into the water area. The slight distortion of ![]() ${\bf I}_{\bf 6}^{\bf R} $ resulted from the fact that after edge
${\bf I}_{\bf 6}^{\bf R} $ resulted from the fact that after edge ![]() ${\bf I}_{\bf 2}^{\bf R} $ only the plotline pixels could gain gradient value
${\bf I}_{\bf 2}^{\bf R} $ only the plotline pixels could gain gradient value ![]() $\left\vert {\nabla \left( {i,j} \right)} \right\vert$ to an acceptable level for hysteretic interval edging (30;60). These results indicate the effectiveness of the algorithm applied for edge detection (presented in Section 3).
$\left\vert {\nabla \left( {i,j} \right)} \right\vert$ to an acceptable level for hysteretic interval edging (30;60). These results indicate the effectiveness of the algorithm applied for edge detection (presented in Section 3).
Two other preferred images are presented in Figures 21 and 22. In this case real images were recorded at time t = 750 s and t = 1500 s, which were time intervals when position accuracy was low.

Figure 21. Real Image ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and
${\bf I}_{\bf 2}^{\bf R} $ after masking and ![]() ${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best fitted map image
${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best fitted map image ![]() ${\bf I}_{\bf 1}^{\bf A} $ at time t = 750s.
${\bf I}_{\bf 1}^{\bf A} $ at time t = 750s.

Figure 22. Real Image ![]() ${\bf I}_{\bf 2}^{\bf R} $ after masking and
${\bf I}_{\bf 2}^{\bf R} $ after masking and ![]() ${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best fitted map image
${\bf I}_{\bf 6}^{\bf R} $ at the end converted and the best fitted map image ![]() ${\bf I}_{\bf 1}^{\bf A} $ at time t = 1500s.
${\bf I}_{\bf 1}^{\bf A} $ at time t = 1500s.
One conclusion can be drawn from the analysis of the results: both real pictures were different. As seen in Figure 21, the differences were caused by a shadow on the harbour. An additional factor affecting Figure 22 was the masking that cut across the real image and intercepted the harbour line. Another factor was the Sun's rays reflecting on the water's surface. This proves that the edge detection algorithm is somewhat prone to such forms of disturbance.
Of course, such disturbances are not possible for radar images. However, despite the growth of the average error value of the position based on real SCCS images, this method is much more precise than those based on radar observations. Elements introducing radar image distortions include radar echoes from other moving floating units. For low observation scopes and for close distances, echoes introduce significant distortions. This is illustrated in Figure 23.

Figure 23. Radar image disturbed by radar echo from a foreign unit and more adjusted to it map image.
Figure 24 shows distance to the reference ![]() $\left( {\varphi _t^T, \lambda _t^T} \right)$ from the position (ϕ t, λ t) determined by the use of r k in consecutive seconds.
$\left( {\varphi _t^T, \lambda _t^T} \right)$ from the position (ϕ t, λ t) determined by the use of r k in consecutive seconds.

Figure 24. Graphical representation of distance to the referential ![]() $\left( {\varphi _t^T, \lambda _t^T} \right)$ from the position (ϕt, λ t) determined by the use of r k in consecutive seconds t = 1, 2…1560.
$\left( {\varphi _t^T, \lambda _t^T} \right)$ from the position (ϕt, λ t) determined by the use of r k in consecutive seconds t = 1, 2…1560.
Like Figure 18, Figure 25 shows the maximum linear correlative factor value, r k, between the best fitted map image and the real image recorded by SCCS.

Figure 25. Graphical representation of linear correlative factor r k of image ![]() ${\bf I}_{\bf 1}^{\bf A} $ most fitted to image
${\bf I}_{\bf 1}^{\bf A} $ most fitted to image ![]() ${\bf I}_{\bf 6}^{\bf R} $ in consecutive seconds t = 1, 2…1560.
${\bf I}_{\bf 6}^{\bf R} $ in consecutive seconds t = 1, 2…1560.
The mean error value of position coordinates (ϕ t, λ t) determined by the use of r k amounted to 6·24 m.
Based on the analysis of Figures 24 and 25, it can be asserted that, as was the case for the minimal maladjustment factor r m, there is a connection between the linear correlative factor value, r k, of images ![]() ${\bf I}_{\bf 1}^{\bf A} $ and
${\bf I}_{\bf 1}^{\bf A} $ and ![]() ${\bf I}_{\bf 6}^{\bf R} $, and the accuracy of position determination. Figure 24 contains local extremes at which position precision is either minimal or maximal; these points are consistent with the linear correlative factor value, r k. In Figure 25, the accuracy in position localisation indicated by the linear correlative factor value was lower than the precision attained by using the minimal maladjustment factor. This is clearly visible from the graphical representation of estimated position recession from the referential position (Figures 17 and 24), and also from the average error value of the position (for r m at 5·72 m, and for r k at 6·24 m). On Figures 24 and 25, respectively, it can be seen that the time intervals in which position accuracy increases or decreases are almost identical to the intervals seen in Figures 17 and 18. This supports the contention that both measures of similarity assessment, r m and r k, react identically to the distortion affecting real images.
${\bf I}_{\bf 6}^{\bf R} $, and the accuracy of position determination. Figure 24 contains local extremes at which position precision is either minimal or maximal; these points are consistent with the linear correlative factor value, r k. In Figure 25, the accuracy in position localisation indicated by the linear correlative factor value was lower than the precision attained by using the minimal maladjustment factor. This is clearly visible from the graphical representation of estimated position recession from the referential position (Figures 17 and 24), and also from the average error value of the position (for r m at 5·72 m, and for r k at 6·24 m). On Figures 24 and 25, respectively, it can be seen that the time intervals in which position accuracy increases or decreases are almost identical to the intervals seen in Figures 17 and 18. This supports the contention that both measures of similarity assessment, r m and r k, react identically to the distortion affecting real images.
5. CONCLUSIONS
On the basis of empirical research, the following hypothesis is supported.
The accuracy of estimating the coordinates of a ship manoeuvring in port using the map image to shoreline image correlation method (as generated from an ENC and compared to real camera images) may be quite high. The accuracy in this study was about 6 m (RME). For comparison purposes, the error of positions estimated by radar observations is a few times higher (about 26 m). This improvement of precision in estimating precision was anticipated, because of the reduction or complete elimination of the factors that affect it negatively.
This study showed that the most important factors affecting the accuracy of position estimates are:
5.1. The quality of the shoreline image in real images
The quality of a real shoreline image depends mainly on the number of distortions affecting it. Such distortions can be caused by the shadow of the ship on the harbour, as well as by the reflection of the Sun's rays off the water surface. For these reasons, the quality of shoreline detection should be associated with modification of edge detection methods and minimising defined distortion.
5.2. Irregular shoreline shape
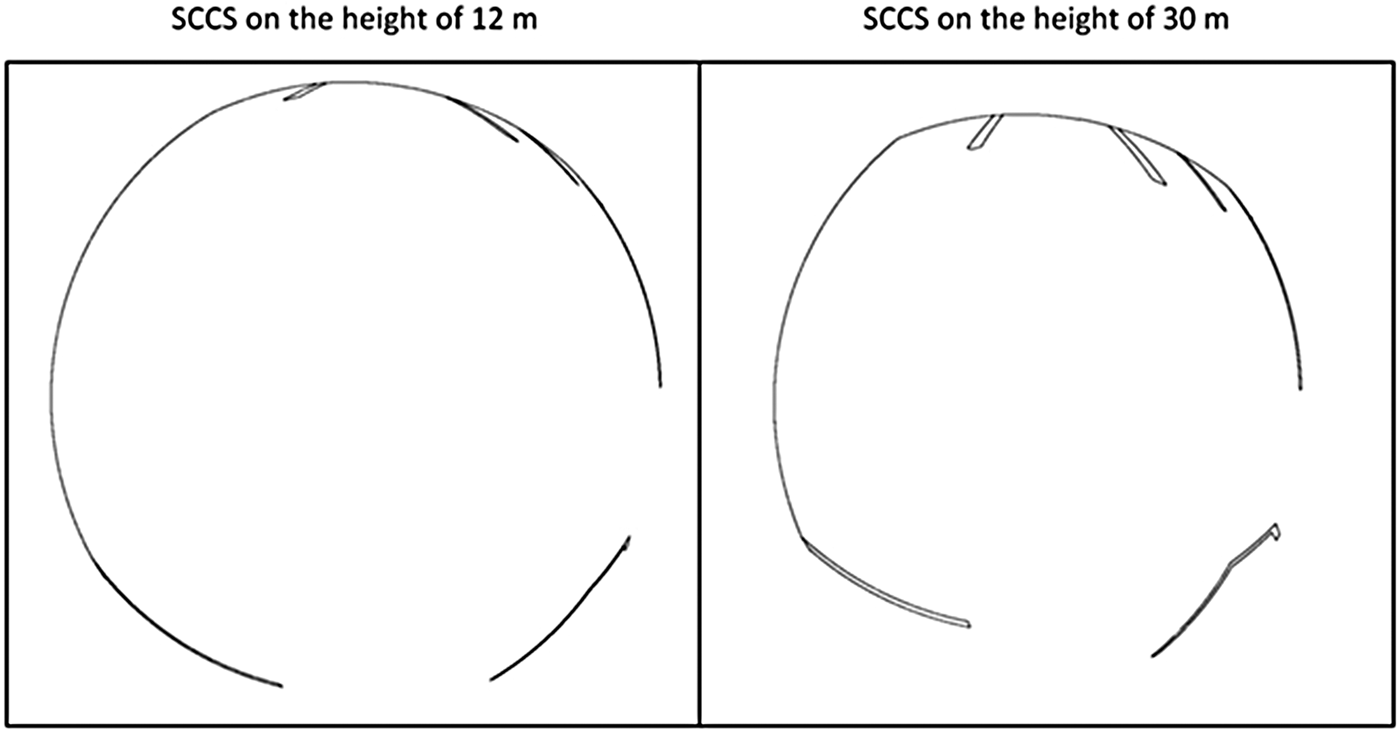
Irregular shoreline features cannot be changed. However, ENC-based analysis can be conducted on the level of irregularity of shoreline objects present in a given port, and on that basis subject them to prognosis. In addition, the height of the SCCS montage on board can be lengthened (measured height against water surface reflection). The benefits obtained by such manipulations are shown in Figure 26.

Figure 26. The same map image ![]() ${\bf I}_0^{\bf A} $ generated from SCCS fixed at the height of 12 m (left) and 30 m (right) above water level.
${\bf I}_0^{\bf A} $ generated from SCCS fixed at the height of 12 m (left) and 30 m (right) above water level.
5.3. Accuracy of Coordinate Points Representing Shoreline Objects in ENC
The precision of coordinate points (knots) representing shorelines in ENC is theoretically dependent on the compilation scales of the ENC (IHO-2, 2002). When ports are involved, we witness enhanced scales of ENC compilation, often 1:5 000, 1:10 000, or 1:15 000. A scale of 1:5 000 and a resolution of 360 dpi pixels represents about 3·5 m on a map image. Accuracy of coded coordinate points in ENC is actually significantly higher. This is a result of the fact that the appliance currently used for port land surveying measures position coordinates with accuracy in terms of millimetres.
For that, map images can be generated at a much larger scale. For 1:500 scale and a resolution of 360 dpi, it is possible to obtain a map image with a pixel representation of about 0·4 m. In such a case, it should be noted that a HD camera would then record a circular image within an area of a mere 216 m2.
5.4. Course measurement accuracy
Error in course estimation certainly has an influence on the disparity between a map image rotation (rotating in line with course) and a real image. It also influences the malfunction of the entire comparing and position-plotting algorithm, thereby resulting in a large error margin. Regarding the use of a ship's gyrocompass, the maximal difference in rotation might even be 3° with a 99% probability. This approximates to a 3 RME course estimation with this appliance.
The effect of this error was greater when the ship was manoeuvring at a large distance from the port area (edges for comparison were at the borders of images). The effect of the error decreased during manoeuvres close to the port area (edges for comparison were closer to the middle of the images).
Position estimates based on radar images were relatively imprecise. The value of the average error of the position estimates indicated that this method cannot be used in the case of manoeuvring the unit in tightly confined port basins (for example, while mooring or approaching the quay). Using the video system makes such manoeuvres feasible. However, the algorithm used in this work for estimating position (Figure 9) entails very complex calculations. This is mainly as the result of the necessity of generating and comparing a large number of map images with the real images. For example, to estimate a position at a distance of 25 m from the point of a similar distance (for an area of a square shape) with a 10 cm resolution capacity (establishing offset Δ of a slide between map images), it is necessary to generate and compare 250,000 map images with the real images. For this reason the algorithm must be optimised before undertaking practical application. This optimisation might entail the use of a few resolution levels for image generation (use of so-called hierarchical method) (Naus and Wąż, Reference Naus and Wąż2012). On the level of low general resolution (Δ = 50 m), through intermediate levels, to the highest, most detailed level of resolution (Δ = 0.1 m), the area of position localisation can be gradually diminished (lessening the length of r for the position localisation circle). In this way, the total number of map images generated for specific levels of resolution would be much smaller than the number of all map images generated for only one resolution at the highest level.
Furthermore, optimisation might entail solving the average error in determining position using the image comparison method. This is so because its value might also be dependent on the length of radius in the position-plotting circle, thereby increasing the possibility of locating the ship's real position on the circle. The radius might be equal to the ratio of ~3 RME in position determination, which in turn is equal to a 99% probability of localising of the ship's real position on the circle.
ACKNOWLEDGMENTS
The paper was prepared in framework of the author's research on “Application of the optical systems to automation of coastal navigation processes” at the Institute of Navigation and Hydrography, Polish Naval Academy.