1. INTRODUCTION
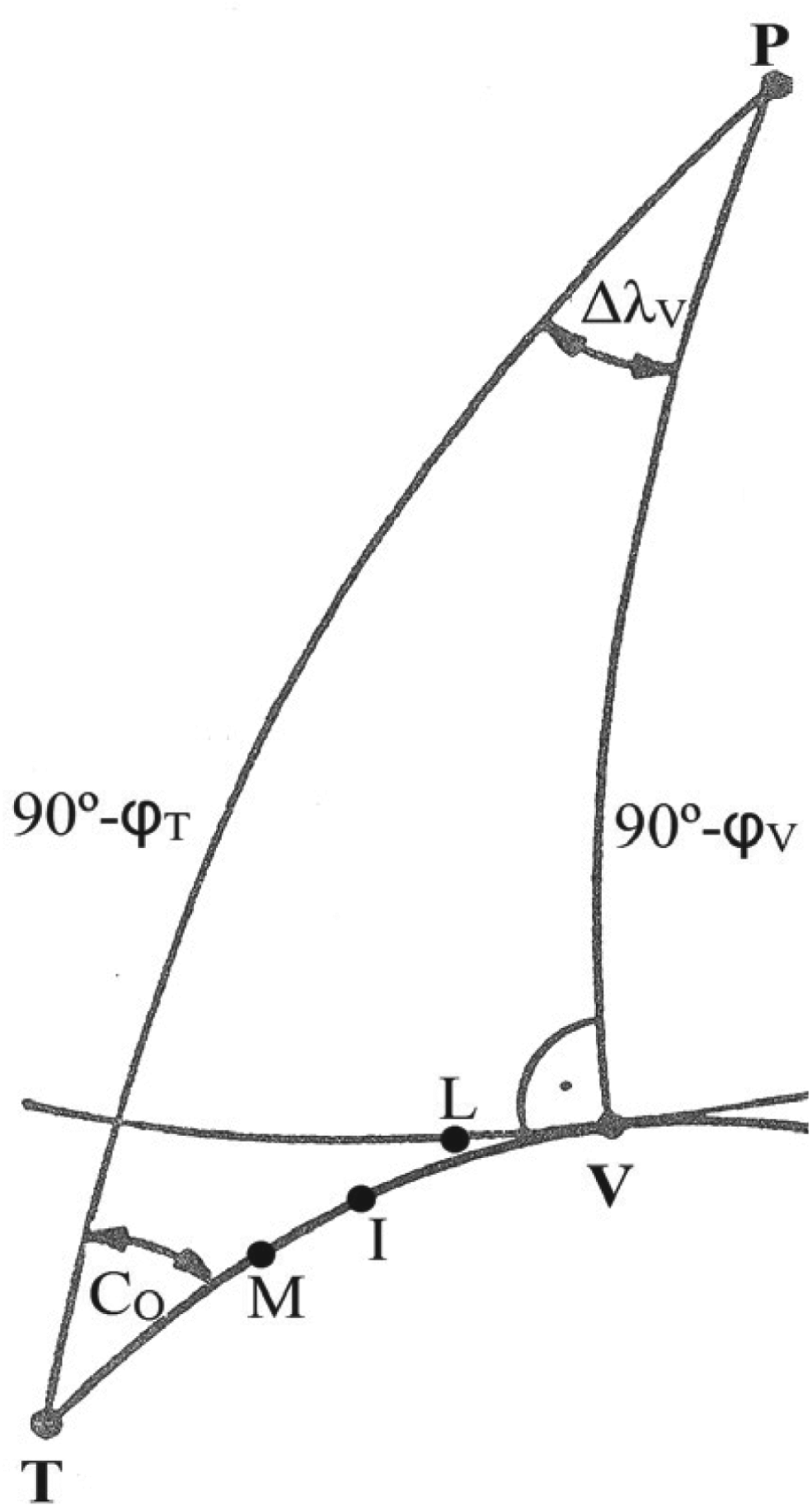
The loxodrome is a transcendental curve spiralling between the north pole and the south pole. The orthodrome (Great Circle) is the intersection of the sphere with a plane containing the centre of the sphere. An intrinsic property of these two curves can be found by Napier's Rules of Circular Parts that have been widely used in navigation. The following problem will demonstrate their advantage. Finding the infinitesimal distance dD O that the vessel must cover in Great Circle sailing for the orthodromic course to change by a small value dD O illustrates the problem. Referring to Figure 1, from a spherical right angled triangle TVP with any two parts given any third can be found as follows:
Having differentiated the expression (1) with respect to the geographic latitude (φ), as C O=C O(φ) and D O=D O(φ) obtains:
From the same triangle:
and
Thus, inserting Equations (3) and (4) in Equation (2) it becomes:
When φ equals φ V, dCO=−dD O tanφ V. For φ=0, dC O=0 showing no course change at the intersection with the equator (node point). Finally, transposing Equation (5) gives an answer to the above problem i.e. for the unit course alteration the unit distance is defined:
Since the orthodrome is a curved line whose true direction changes continually (except for a meridian or the equator), a number of points along the Great Circle are selected, connected by loxodromes and followed by rhumb line courses.

Figure 1. Middle Latitude Rule on a Sphere.
2. ANALYSIS
2.1. Middle latitude rule for the sphere
Equation (4) is of a particular interest as it gives an orthodromic course at any latitude (0⩽φ⩽φ V) once vertex latitude is known. Introducing Middle latitude (M) at which the arc length of the parallel is equal to the departure in proceeding between two points, shown with the relation:
Equation (4) gives orthodromic course at Middle latitude:
where:
DLat-Difference of Latitude,and
DMP-Difference of Meridional Parts for the Sphere.
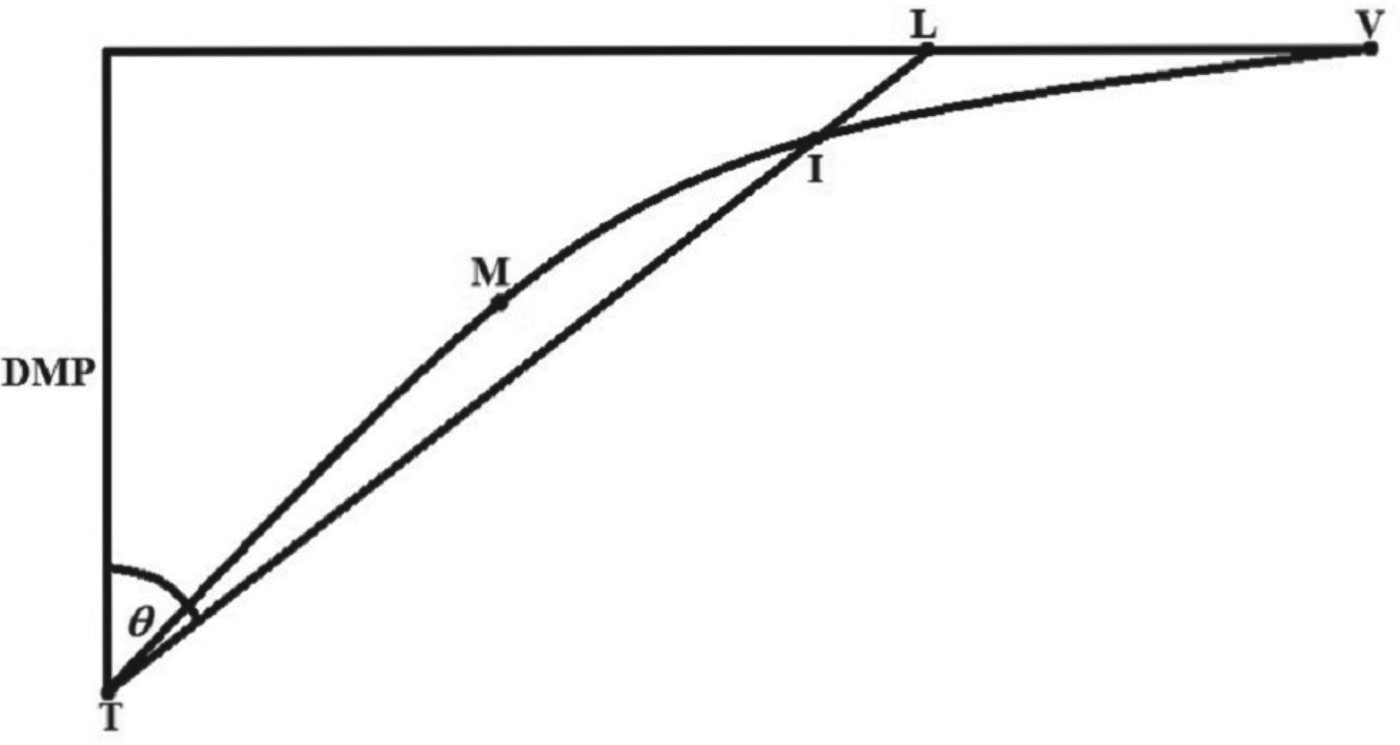
Taking ![]() $C_{O_{Mid}} $ as an initial rhumb line course (θ T) from the point of departure (T) leads to the intersection (I) of a loxodrome with an orthodrome (Great Circle) as shown in Figure 2. As determination of the intersection of the orthodrome and the loxodrome cannot be formulated in a closed form, an iterative solution is to be derived. Transcendental equation:
$C_{O_{Mid}} $ as an initial rhumb line course (θ T) from the point of departure (T) leads to the intersection (I) of a loxodrome with an orthodrome (Great Circle) as shown in Figure 2. As determination of the intersection of the orthodrome and the loxodrome cannot be formulated in a closed form, an iterative solution is to be derived. Transcendental equation:
(λ 0 – equatorial intersection longitude of the loxodrome) and its derivatives with respect to λ I :
form a base for an iterative solution of intersection using the Newton-Raphson method. If ![]() $\varphi _T = 0 \Rightarrow \lambda _T = \lambda _0 $. In order to use the above formulae for all quadrants, the difference of longitude sign (∼) represents the shorter arc of the equator between the two meridians. Vertex latitude (φ V) is taken as an absolute value while the rhumb line course is
$\varphi _T = 0 \Rightarrow \lambda _T = \lambda _0 $. In order to use the above formulae for all quadrants, the difference of longitude sign (∼) represents the shorter arc of the equator between the two meridians. Vertex latitude (φ V) is taken as an absolute value while the rhumb line course is ![]() $\left( {0 \lt \theta _T \lt {\textstyle{\pi \over 2}}} \right)$. Thus, determining the zero of f(λ I) crossing is obtained. As an initial approximation for the longitude of intersection (λ I) geographic longitude (λ 1) which satisfies the condition f(λ 1)·f″(λ 1)>0 is to be used.
$\left( {0 \lt \theta _T \lt {\textstyle{\pi \over 2}}} \right)$. Thus, determining the zero of f(λ I) crossing is obtained. As an initial approximation for the longitude of intersection (λ I) geographic longitude (λ 1) which satisfies the condition f(λ 1)·f″(λ 1)>0 is to be used.
If f(λ 2) using Equation (12) is larger than the allowed error (E=10−6), λ 2 is taken as the approximation and the iteration process is repeated until the error falls below E. The iterations converge in a few steps. With current computer capabilities, the procedure can be completed within a fraction of a second.

Figure 2. Middle Latitude Rule on a Mercator chart.
In the examples presented in Table 1, the Greenwich meridian is taken as a longitude of departure (λ T=0), while θ I represents a rhumb line course connecting intersection point (I) with vertex (V). Distance (D TLV) is based on rhumb line (θ T) sailing to vertex latitude then due east (or west) along parallel to vertex. The shorter distance (D TIV) is obtained if course is altered to rhumb line (θ I) at I, then proceeding towards the vertex. Great Circle Distance (D GC) serves as a reference value.
Table 1. Middle Latitude Rule (Sphere).

For practical navigation the latitudes of points on the Great Circle track for equal Difference of Longitude (DLo) intervals from Vertex (usually 5°) are transferred from a Gnomonic to a Mercator chart and connected by rhumb lines. One of these legs cuts the said loxodrome near to the calculated value of I (Figure 2). The smaller is the interval DLo from the Vertex, the more accurate intersection point (I) on the Mercator chart is obtained.
2.2. Middle latitude rule for the spheroid
By introducing Difference of Latitude Parts (DLP) and Difference of Meridional Parts (DMP) for the oblate Earth, with a slight modification the method may be used on the rotational ellipsoid (spheroid). Specifically, Equation (7) becomes:
and consequently modified Equation (8) gives the geodesic course at Middle latitude:
As the geodesic (line) on the spheroid is defined by differential equations, finding its vertex longitude and intersection with a loxodrome will require a different mathematical model and a more laborious calculation, which falls beyond the scope of this article.
3. CONCLUSION
The mathematical tools i.e. Napier's Rules of Circular Parts and Newton-Raphson method have been well known since the 17th century and are still very relevant. The study gives a few findings worth remembering:
• To reach Great Circle vertex in two steps with minimum distance, the initial rhumb line course (θ T) must be equal to the orthodromic course at the Middle latitude
 $(C_{O_{Mid}} )$.
$(C_{O_{Mid}} )$.• The method finds a turn point (I) from where a rhumb line course (θ I) is followed towards vertex which gives a further reduction in the overall distance as inferred in the paper (Han-Fei et al., Reference Han-Fei Lu and Chiang1991).
• The higher the Middle latitude the more distance will be saved on the sphere.
ACKNOWLEDGMENT
The author is indebted to Professor Tibor K. Pogány for the useful insights and constructive remarks while preparing this article.