Published online by Cambridge University Press: 13 September 2024
Unmanned aerial vehicles (UAVs) have recently been widely applied in a comprehensive realm. By enhancing computer photography and artificial intelligence, UAVs can automatically discriminate against environmental objectives and detect events that occur in the real scene. The application of collaborative UAVs will offer diverse interpretations which support a multiperspective view of the scene. Due to the diverse interpretations of UAVs usually deviating, UAVs require a consensus interpretation for the scenario. This study presents an original consensus-based method to pilot multi-UAV systems for achieving consensus on their observation as well as constructing a group situation-based depiction of the scenario. Taylor series are used to describe the fuzzy nonlinear plant and derive the stability analysis using polynomial functions, which have the representations $V(x )={m_{\textrm{1} \le l \le N}}({{V_\textrm{l}}(x )} )$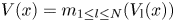 and ${V_l}(x )={x^T}{P_l}(x )x$
and ${V_l}(x )={x^T}{P_l}(x )x$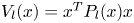 . Due to the fact that the ${\dot{P}_l}(x )$
. Due to the fact that the ${\dot{P}_l}(x )$ in ${\dot{V}_l}(x )={\dot{x}^T}{P_l}(x )x + {x^T}{\dot{P}_l}(x )x + {x^T}{P_l}(x )\dot{x}$
in ${\dot{V}_l}(x )={\dot{x}^T}{P_l}(x )x + {x^T}{\dot{P}_l}(x )x + {x^T}{P_l}(x )\dot{x}$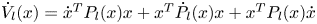 will yield intricate terms to ensure a stability criterion, we aim to avoid these kinds of issues by proposing a polynomial homogeneous framework and using Euler's functions for homogeneous systems. First, this method permits each UAV to establish high-level conditions from the probed events via a fuzzy-based aggregation event. The evaluated consensus indicates how suitable is the scenario collective interpretation for every UAV perspective.
will yield intricate terms to ensure a stability criterion, we aim to avoid these kinds of issues by proposing a polynomial homogeneous framework and using Euler's functions for homogeneous systems. First, this method permits each UAV to establish high-level conditions from the probed events via a fuzzy-based aggregation event. The evaluated consensus indicates how suitable is the scenario collective interpretation for every UAV perspective.