1. INTRODUCTION
Since the first close-up picture of Mars was obtained by the National Aeronautics and Space Administration (NASA) in 1965, the Red Planet has become the focus of an intensive series of missions for many decades, evolving from flybys to orbiters and rovers. The great success of previous and recent Mars exploration missions, such as Mars Express and the Mars Science Laboratory, has significantly increased the understanding of the Earth-like planet. In the future, Mars explorations may bring samples of Mars back to Earth and eventually establish a manned presence upon the Martian surface.
An essential contributing factor to the success of Mars exploration missions is a high-precision deep-space navigation system. Generally, navigation support for a Mars exploration mission is primarily provided by the NASA's Deep Space Network (DSW). Using two-way Doppler and range data between the user and DSW stations, spacecraft trajectory can be determined either on board the spacecraft or at ground stations (Cangahuala, Reference Cangahuala2000; Thornton and Border, Reference Thornton and Border2003). In order to improve the navigation performance by efficiently determining spacecraft angular position in the plane of the sky, the Delta Differential One-Way Ranging (Delta-DOR) technique is also employed by some missions, such as the Mars Odyssey and the Mars Exploration Rovers (Antreasian et al., Reference Antreasian, Baird, Border, Burckhart, Graat, Jah, Mase, McElrath and Portock2005; D'Amario, Reference D'Amario2006). With the expansion of science activities on Mars, NASA's Jet Propulsion Laboratory has begun to develop a Mars communication and navigation orbital infrastructure (Bell et al., Reference Bell, Cesarone, Ely, Edwards and Townes2000). Besides that, some autonomous navigation strategies are also proposed to support future Mars exploration missions (Ely et al., Reference Ely, Duncan, Lightsey and Mogensen2006; Cui et al., Reference Cui, Yu, Zhu and Gao2013).
In Zhang and Xu (Reference Zhang and Xu2014), a novel navigation architecture-based libration point satellite constellation was proposed to construct the Universe Lighthouse for deep-space navigation. Due to strong asymmetry of the three-body force field, orbits of libration point satellites can be determined autonomously by the Liaison technique. Moreover, as the baseline length is much longer than that of the traditional navigation system, the proposed system is more suitable for deep-space navigation. The autonomy and feasibility of the libration point satellite navigation system have been verified by many scholars. Hill (Reference Hill2007) conducted a systematic study on the autonomous orbit determination of libration point satellites in his PhD dissertation. Gao et al. (Reference Gao, Xu and Zhang2014) analysed the orbit determination accuracy of different constellation configurations for the libration point satellite navigation system. Superiorities of using libration point satellites for cislunar navigation have also been proved by Parker et al. (Reference Parker, Leonard, Fujimoto, McGranaghan, Born and Anderson2013), Leonard et al. (Reference Leonard, Parker, Anderson, McGranaghan, Fujimoto and Born2013) and Zhang and Xu (Reference Zhang and Xu2015), respectively.
Based on and beyond these previous works, a feasibility study of using the libration point satellite navigation system to support future Mars exploration is conducted in this paper. By developing a high-fidelity Mars exploration mission scenario, navigation performance of the candidate Earth-Moon L 1,2,4,5 four-satellite constellation is evaluated by Monte-Carlo (MC) simulations. In addition, the effects of different measurement types (range, range-rate, range and range-rate) are also considered and compared.
To this end, the remainder of this paper is organised as follows. In Section 2, a brief review of the libration point satellite navigation system is given. After describing the reference Mars exploration mission scenario, a spacecraft dynamic model and navigation measurements are explained in Section 3 and Section 4 gives a detailed description of the novel adaptive unscented Kalman filter algorithm adopted in this work. After that, in Section 5, Mars navigation results are presented and analysed for different mission phases and measurement types. Finally, some brief conclusions are drawn in Section 6.
2. LIBRATION POINT SATELLITE NAVIGATION SYSTEM
The libration point satellite navigation system is a novel navigation architecture that consists of satellites located in periodic orbits around the Earth-Moon libration points. The main advantages of this system lie in its autonomy and extended navigation capability, which have been verified in our previous works. As the main focus of this study, the Earth-Moon L 1,2,4,5 four-satellite constellation is selected as the basis for Mars navigation performance analysis and the candidate navigation architectures are summarised in Table 1 (Zhang and Xu, Reference Zhang and Xu2014).
Table 1. Candidate navigation architectures of the Earth-Moon L 1,2,4,5 four-satellite constellation.
The variables A H, APL, AVL, and A VP in the table are amplitude parameters respectively representing the out-of-plane amplitude of the Halo orbit (H), the in-plane amplitude of the Planar Lyapunov orbit (PL), the out-of-plane amplitude of the Vertical Lyapunov orbit (VL) and the out-of-plane amplitude of the Vertical Periodic orbit (VP). These amplitude parameters will be used to construct the Libration Point Orbits (LPOs) and the construction details can be found in Lei et al. (Reference Lei, Xu, Hou and Sun2013a) and Lei and Xu (Reference Lei and Xu2013b).
Since the LPOs can be autonomously determined by the Liaison technique, positions and velocities of the libration point navigation satellites can be considered as known with implicit errors. Consequently, their “accurate” broadcast ephemeris will be used as given parameters in the navigation simulation process.
3. REFERENCE SCENARIO AND MODEL
In this section, a detailed description of the reference mission scenario is given, including the dynamic model and navigation measurements.
3.1. Reference Mission Scenario
According to the operation of a Mars exploration mission, the reference scenario considered in this work mainly consists of four mission phases: Earth departure phase, Earth-Mars transfer phase, Mars approach phase and Mars orbit phase. Definitions of the four phases are given in Table 2.
Table 2. Reference mission phase definition.
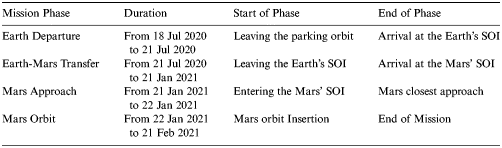
The Earth departure phase begins with a hyperbolic escape manoeuvre of about 3·81 km/s at 18 July 2020 11:42:10 UTC. With this manoeuvre, the spacecraft is delivered into the Earth escape trajectory and the hyperbolic excess velocity at the Earth's Sphere Of Influence (SOI) is approximately 3·73 km/s. The second phase is a heliocentric Earth-to-Mars transfer that ends when the spacecraft reaches Mars' SOI. After approximately 185 days of interplanetary cruise, the spacecraft makes its closest approach to Mars at 22 January 2021 11:54:18 UTC. Meanwhile, a Mars Orbit Insertion (MOI) manoeuvre is performed to insert the spacecraft into a circular target orbit. The magnitude of MOI is approximately 2·44 km/s and parameters of the final Mars orbit are summarised in Table 3.
Table 3. Orbital parameters of the final Mars orbit.
3.2 Spacecraft Dynamic Model
The dynamic model of spacecraft motion during the above mission phases can be approximated by the perturbed two-body problem, which can be expressed in a general form as
$$\ddot{\bi r} = {\bi F}_0 + {\bi F}_\varepsilon $$where F0 = −μ r/r 3 is the two-body acceleration of the central body and Fε is the resultant vector of all the perturbing accelerations.
For the Earth departure phase, the motion of the spacecraft is studied in the Geocentric Celestial Reference Frame (GCRF). Perturbations considered include the non-spherical gravitation of the Earth, the third-body perturbations of the Moon, the Sun and planets, and the non-gravitational perturbation due to solar radiation pressure. The non-spherical gravitation of the Earth can be obtained directly by the potential gradient
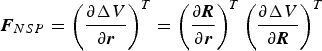$${\bi F}_{NSP} = \left( {\displaystyle{{\partial \Delta V} \over {\partial {\bi r}}}} \right)^T = \left( {\displaystyle{{\partial {\bi R}} \over {\partial {\bi r}}}} \right)^T \left( {\displaystyle{{\partial \Delta V} \over {\partial {\bi R}}}} \right)^T$$
where (∂ R/∂ r)T is the conversion from the Geocentric Terrestrial Reference Frame (GTRF) to the GCRF, and the International Astronomical Union's Standards of Fundamental Astronomy (IAU SOFA) software collection can be conveniently adopted to finish this transformation (IAU SOFA Board, 2010). The non-spherical gravitational potential ΔV is commonly given in terms of spherical harmonics (
$\overline C_{lm} $, 
$\overline S_{lm} $) as
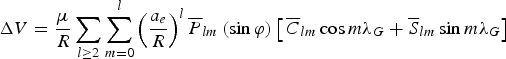$$\Delta V = \displaystyle{\mu \over R}\sum\limits_{l \ge 2} {\sum\limits_{m = 0}^l {\left( {\displaystyle{{a_e} \over R}} \right)^l \overline P_{lm} \left( {\sin \varphi} \right)} \left[ \,{\overline C_{lm} \cos m\lambda _G + \overline S_{lm} \sin m\lambda _G} \right]} $$
where a e is the equatorial radius of the Earth and 
$\bar P_{lm} $ is the normalized associated Legendre polynomial. In this work, the WGS84 gravity field model is adopted for the non-spherical Earth (Defense Mapping Agency, 1984).
The acceleration due to the third bodies can be written in a simple form as
$${\bi F}_{TBP} = - \mu^{\prime}\left( {\displaystyle{{\bf \Delta} \over {\Delta ^3}} + \displaystyle{{{\bi r^{\prime}}} \over {r^{\prime 3}}}} \right)$$where μ′ is the gravitational parameter of the third body; Δ is the position vector from the third body to the spacecraft, and r ′ is the position vector from the Earth to the third body. Here for the Earth departure phase, third bodies considered include the Moon, the Sun and the eight planets except the Earth. Positions of these celestial bodies can be obtained from the JPL DE405 ephemerides (Standish, Reference Standish1998).
Based on a cylindrical shadow model, the non-gravitational perturbation due to solar radiation pressure can be written as
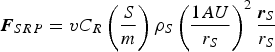$${\bi F}_{SRP} = vC_R \left( {\displaystyle{S \over m}} \right)\rho _S \left( {\displaystyle{{1AU} \over {r_S}}} \right)^2 \displaystyle{{{\bi r}_S} \over {r_S}} $$where rS is the position vector from the Sun to the spacecraft; ρ S = 4·56 × 10−6N/m 2 is the solar radiation pressure constant in the vicinity of Earth; (S/m) is the area-mass ratio of the spacecraft, and C R is the reflectivity coefficient with a value of approximately one. The eclipse factor v = 0 once the spacecraft is in the shadow of the Earth, else v = 1 meaning that the spacecraft is in sunlight.
For the Earth-Mars transfer phase, the gravitational attraction of the Sun becomes the main force acting on the spacecraft and the motion is studied in the International Celestial Reference Frame (ICRF). Major perturbations for the interplanetary cruise phase are the solar radiation pressure and the third-body perturbations of the eight planets and the Moon. Expressions for these perturbations are similar to the Earth departure phase, which is not repeated here for brevity.
After the spacecraft enters the Mars' SOI, the reference frame used to study the motion is changed from the ICRF to the Mars-Centred Mars Mean Equator (MCMME) inertial frame. For the Mars approach phase, which can be regarded as an inverse process of the Earth departure phase, perturbations considered are the third-body perturbations of the Sun and planets, the solar radiation pressure, and the non-spherical gravitation of Mars. By performing the MOI manoeuvre at the closest approach to Mars, the spacecraft is captured into the planned Mars orbit and Mars' oblateness becomes the main perturbation factor for the Mars orbit phase. The Mars gravity field adopted in this work is the Goddard Mars Model 2B (GMM-2B), complete to degree and order 80 (Lemoine et al., Reference Lemoine, Smith, Rowlands, Zuber, Neumann, Chinn and Pavlis2001). Besides that, the third-body perturbation of the Sun should also be taken into account for the Mars orbit propagation.
Based on the above dynamical model, the nominal trajectory of the spacecraft can be obtained by numerical integration of Equation (1). However, considering the existence of un-modelled or mis-modelled accelerations in real missions, a Dynamical Model Error (DME) is introduced to compensate for this acceleration. The order of magnitude of the main perturbations and the DME term compared to the central body gravitation is summarised in Table 4.
Table 4. Order of magnitude of the main perturbations and the DME term.
O(10−n) in the table represents the smaller terms of order 10−n and the magnitude of the DME term is selected sufficiently large to ensure the reliability of the navigation simulation results.
3.3. Navigation Measurement Model
The baseline tracking data considered in this work are traditional range and range-rate measurements, except that the tracking stations have been moved to LPOs. Once a libration point satellite is visible to the user spacecraft, navigation measurements are generated according to the following expressions
$$\rho = \left\vert {{\bi r} - {\bi r}_L} \right\vert + \sigma _{bias}^\rho + \sigma _{noise}^\rho $$
$$\dot \rho = \displaystyle{{\left( {\dot{\bi r} - \dot{\bi r}_L} \right) \cdot \left( {{\bi r} - {\bi r}_L} \right)} \over {\left\vert {{\bi r} - {\bi r}_L} \right\vert}} + \sigma _{bias}^{\dot \rho} + \sigma _{noise}^{\dot \rho} $$where 
$\left( {{\bi r}\comma\, \dot{\bi r}} \right)$ and 
$\left( {{\bi r}_L\comma\,\dot{\bi r}_L} \right)$ are the position and velocity vectors of the user spacecraft and the libration point satellite, respectively. As various errors exist in every observation measurement, two main components are considered in the above expressions. One is the systematic bias σ bias, which is related to the measurement model, and the other is a random white noise σ noise that differs in every measurement. Both of these are drawn from the Gaussian distribution, with zero mean and specific standard deviation.
Using nominal orbits of the user and libration point satellites, navigation measurements can be simulated according to the above expressions. In the following section, a detailed description of the filter algorithm adopted in this work will be given.
4. NAVIGATION FILTER ALGORITHM
The Unscented Kalman Filter (UKF) developed by Julier et al. (Reference Julier, Uhlmann and Durrant-Whyte1995) is a widely used algorithm for nonlinear state estimation. In this work, a novel UKF with adaptation of the Scaling Parameter (SP) is utilised for navigation performance analysis.
The models of spacecraft dynamics and navigation measurements can be approximated by the following stochastic difference equations:
$${\bf x}_{k + 1} = {\bf f}_k \left( {{\bf x}_k} \right) + {\bf w}_k $$
$${\bf z}_k = {\bf h}_k \left( {{\bf x}_k} \right) + {\bf v}_k $$
where 
${\bf x}_k \in \Re ^n $ and 
${\bf z}_k \in \Re ^m $ represent the state and measurement at time instant k, respectively; 
${\bf w}_k \in \Re ^n $ and 
${\bf v}_k \in \Re ^m $ are zero-mean Gaussian white sequences having zero cross-correlation with each other:
$$E\left[ {{\bf w}_k {\bf w}_i^T} \right] = \left\{ \matrix{{\bi Q}_k\comma\, k = i \cr 0\comma\, k \ne i} \right.\semicolon\, E\left[ {\bf v}_k {\bf v}_i^T \right] = \left\{ \matrix{{\bi R}_k\comma\, k = i \cr 0\comma\, k \ne i} \right.\semicolon\, E\left[ {{\bf w}_k {\bf v}_i^T} \right] = 0\comma\, \forall k\comma\, i$$where Qk is the process noise covariance matrix; Rk is the measurement noise covariance matrix.
In the time update step, the (2n+1) sigma points xk −1(i) are selected as follows
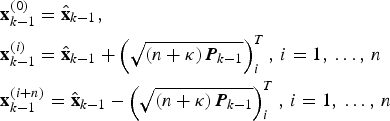$$\eqalign{& {\bf x}_{k - 1}^{(0)} = {\hat{\bf x}}_{k - 1}\comma \cr & {\bf x}_{k - 1}^{(i)} = {\hat{\bf x}}_{k - 1} + \left( {\sqrt {\left( {n + \kappa} \right){\bi P}_{k - 1}}} \right)_i^T\comma\, i = 1\comma\, \ldots\comma\, n \cr & {\bf x}_{k - 1}^{(i + n)} = {\hat{\bf x}}_{k - 1} - \left( {\sqrt {\left( {n + \kappa} \right){\bi P}_{k - 1}}} \right)_i^T\comma\, i = 1\comma\, \ldots\comma\, n} $$where 
${\hat{\bf x}}_{k - 1} $ and Pk −1 are the current best guess of the mean and covariance, respectively; κ is the SP, which can be used to reduce the higher-order errors of the mean and covariance approximation. Here, for the predictive step, a standard value of κ std = 3−n is adopted.
After the sigma points are generated, time update is performed according to the system equation
$${\bf x}_k^{(i)} = {\bf f}_k \left( {{\bf x}_{k - 1}^{(i)}} \right)\comma\, i = 0\comma\, \ldots\comma\, 2n$$Then, using the predicted samples at time instant k, the a priori state and covariance estimates can be obtained by
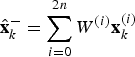$${\hat{\bf x}}_k^ - = \sum\limits_{i = 0}^{2n} {W^{(i)} {\bf x}_k^{(i)}} $$
$${\bi P}_k^ - = \sum\limits_{i = 0}^{2n} {W^{(i)} \left( {{\bf x}_k^{(i)} - {\hat{\bf x}}_k^ -} \right)\left( {{\bf x}_k^{(i)} - {\hat{\bf x}}_k^ -} \right)^T} + {\bi Q}_k $$where W (i) are the weight coefficients defined as
$$\eqalign{& W^{(0)} = \displaystyle{\kappa \over {n + \kappa}}\comma \cr & W^{(i)} = \displaystyle{1 \over {2\left( {n + \kappa} \right)}}\comma\, i = 1\comma\, \ldots\comma \,2n} $$In the measurement update step, a new set of sigma points is generated based on the predicted state estimates:
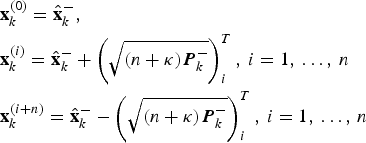$$\eqalign{& {\bf x}_k^{(0)} = {\hat{\bf x}}_k^ -\comma \cr & {\bf x}_k^{(i)} = {\hat{\bf x}}_k^ - + \left( {\sqrt {\left( {n + \kappa} \right){\bi P}_k^ -}} \right)_i^T\comma\, i = 1\comma\, \ldots\comma\, n \cr & {\bf x}_k^{(i + n)} = {\hat{\bf x}}_k^ - - \left( {\sqrt {\left( {n + \kappa} \right){\bi P}_k^ -}} \right)_i^T\comma\, i = 1\comma\, \ldots\comma\, n} $$Then the predicted measurement can be obtained by
$${\hat{\bf z}}_k (\kappa ) = \sum\limits_{i = 0}^{2n} {W^{(i)} {\bf z}_k^{(i)}} = \sum\limits_{i = 0}^{2n} {W^{(i)} {\bf h}_k \left( {{\bf x}_k^{(i)}} \right)} $$It should be noted that the SP in the measurement update step is not set to the standard value, but adapted according to the following criterion
$$\kappa _k^{opt} = \arg \mathop {\min} \limits_\kappa \left[ {{\tilde{\bf z}}_k (\kappa )^T {\bi R}_k^{ - 1} {\tilde{\bf z}}_k (\kappa )} \right]$$
where 
${\tilde{\bf z}}_k (\kappa ) = {\bf z}_k - {\hat{\bf z}}_k (\kappa )$ is the measurement prediction error for a given SP; the measurement noise covariance matrix Rk is introduced for normalisation. Based on the above criterion, an optimal SP minimising the normalised squared measurement prediction error can be obtained, and the quality of the UKF estimation can be improved accordingly (Straka et al., Reference Straka, Duník and Šimandl2014). In this work, a cooperative evolutionary algorithm combining particle swarm optimisation with differential evolution is employed for the SP adaptation (Lei et al., Reference Lei, Xu and Sun2013c).
Using the optimal value of SP, the predicted measurement covariance and the cross covariance can be computed by
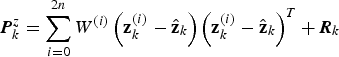$${\bi P}_k^z = \sum\limits_{i = 0}^{2n} {W^{(i)} \left( {{\bf z}_k^{(i)} - {\hat{\bf z}}_k} \right)\left( {{\bf z}_k^{(i)} - {\hat{\bf z}}_k} \right)^T} + {\bi R}_k $$
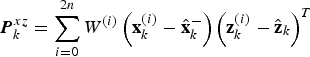$${\bi P}_k^{xz} = \sum\limits_{i = 0}^{2n} {W^{(i)} \left( {{\bf x}_k^{(i)} - {\hat{\bf x}}_k^ -} \right)\left( {{\bf z}_k^{(i)} - {\hat{\bf z}}_k} \right)^T} $$Finally, the measurement update of the UKF can be finished using the normal Kalman filter equations:
$${\bi K}_k = {\bi P}_k^{xz} \left( {{\bi P}_k^z} \right)^{ - 1} $$
$${\hat{\bf x}}_k = {\hat{\bf x}}_k^ - + {\bi K}_k \left( {{\bf z}_k - {\hat{\bf z}}_k} \right)$$
$${\bi P}_k = {\bi P}_k^ - - {\bi K}_k {\bi P}_k^z {\bi K}_k^T $$5. SIMULATION RESULTS AND ANALYSIS
According to the reference mission scenario and navigation model, a Mars navigation simulation is conducted for the candidate Earth-Moon L 1,2,4,5 four-satellite constellations. Table 5 summarises the initial state and measurement uncertainties used throughout the simulation.
Table 5. Initial state and measurement uncertainties used throughout the simulation.
From the table, it can be seen that a (10 m, 0·3 mm/s) systematic bias is used to corrupt the measurement data. Besides, a (10 m, 0·3 mm/s) white noise is considered to compensate for the stochastic error. Based on the above parameters, navigation performance of the candidate constellations is analysed respectively for the four mission phases.
5.1. Earth Departure Navigation Performance
As a starting point, the Earth departure phase is studied. After generating the nominal trajectory for the user spacecraft, an observability analysis is performed first. Figure 1 illustrates the timeline of visible libration point satellites during the Earth departure phase.
Figure 1. Timeline of visible libration point satellites during the Earth departure phase.
It can be seen from Figure 1 that only the L 5 navigation satellite is in the user's field of view during the first 10 minutes. After that, the L 1, L 2 and L 4 navigation satellites are successively visible, and 40 minutes later, all of the four libration point navigation satellites are available to the user spacecraft. Once a libration point satellite is visible, navigation measurements can be generated according to the previous descriptions. Here for the Earth departure phase, range and range-rate measurements are simulated at 10-minute intervals. Then, with the use of the adaptive UKF, Earth departure phase navigation performance is evaluated by MC simulations.
Figure 2 shows the navigation results of the Halo-Halo-VP-VP constellation (ID = 1). The obtained Root-Mean-Square (RMS) position error for the Earth departure phase is 15·1 m and the obtained RMS velocity error is 3·9 mm/s. The state estimation error is well-bounded by the 3σ line, with a probability of 98·96%, 99·74% and 100%, respectively for the x, y and z components falling inside the 3σ line, and 98·96%, 98·19% and 98·45%, respectively for the vx, vy and vz components falling inside the 3σ line. In addition, it can also been noticed from the figure that the z-axis state estimation error is much larger than the other two directions, and this may be related to the limited variation of observation geometry out of the xy plane. In order to compare the navigation performance of different constellation configurations, we perform N = 1000 identical MC simulations for every candidate Earth-Moon L 1,2,4,5 four-satellite constellation. Besides that, the effects of different measurement types (range only, range-rate only, range & range-rate) are also considered and the final results are summarised in Table 6.
Figure 2. State estimation error for the Earth departure phase (Halo-Halo-VP-VP constellation).
Table 6. Navigation results for the Earth departure phase (N = 1000 MC runs).
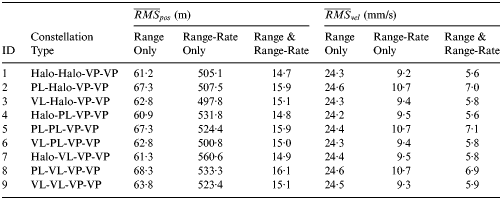
From the results, it can be found that the average RMS position error and velocity error for the Earth departure phase changes slightly with the constellation configuration, but varies dramatically with the measurement type. When only range or range-rate measurements are used, the resulting navigation performance is apparently worse, with the former having a larger velocity estimation error and the latter having a larger position estimation error. Considering the property of these two measurement types, the combined tracking data may contribute to a better navigation performance, and this has been verified by the simulation results. When the combined range and range-rate measurements are used for Earth departure navigation, the resulting average RMS position error can be reduced to 15 m and the average RMS velocity error can be reduced to 6 mm/s. Consequently, it may be concluded that the combined range and range-rate measurements are the most suitable tracking data for Earth departure phase navigation.
5.2. Earth-Mars Transfer Navigation Performance
After discussing the Earth departure phase, we go on to study the navigation performance during the Earth-Mars transfer phase. The observability analysis result indicates that the four libration point navigation satellites are always available during the interplanetary cruise. Therefore, range and range-rate measurements can be continuously generated. Here, for the Earth-Mars transfer phase, observations are taken and processed at 12 hour intervals throughout the 184 day arc.
By using the adaptive UKF, navigation performance of the Halo-Halo-VP-VP constellation (ID = 1) is shown in Figure 3. The RMS position error for the Earth-Mars transfer phase is 2385·9 m and the RMS velocity error is 1·2 mm/s. The probability of the position estimation error falling inside the 3σ line is 99·18%, 100% and 99·73%, respectively for the x, y and z components, while the probability of the velocity estimation error falling inside the 3σ line is 100% for each component. Besides, it can be noted that the x-axis state estimation error is much smaller than the other two directions, and this is also due to the relatively large variation of observation geometry in the x-direction. Similar simulations are conducted for the other candidate Earth-Moon L 1,2,4,5 four-satellite constellations and the navigation results are summarised in Table 7.
Figure 3. State estimation error for the Earth-Mars transfer phase (Halo-Halo-VP-VP constellation).
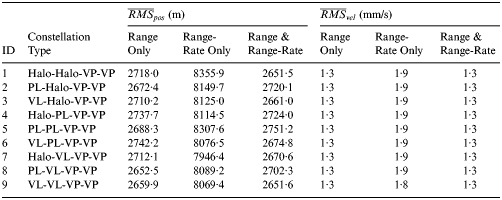
Table 7. Navigation results for the Earth-Mars transfer phase (N = 1000 MC runs).
It can be seen that the navigation performance of different constellations is also similar for the Earth-Mars transfer phase. For most constellation configurations, the best navigation accuracy is achieved by the combined range and range-rate measurements, with the average RMS position error about 2660 m and the average RMS velocity error about 1·3 mm/s. But when the L 1 navigation satellite is located in the planar Lyapunov orbit (that is, the ID = 2, 5, 8 constellation), range only measurements give the best results. When only range-rate measurements are used for Earth-Mars transfer navigation, the resulting state estimation error is always the largest. Therefore, the appropriate tracking data for interplanetary cruise navigation is range or combined range and range-rate measurements.
5.3. Mars Approach Navigation Performance
The third study phase is the Mars final approach. Similarly to the interplanetary cruise phase, the four libration point navigation satellites are continuously visible during the Mars approach phase. Therefore, range and range-rate measurements are simulated at 10 minute intervals after the spacecraft enters Mars' SOI and the navigation performance of the Halo-Halo-VP-VP constellation (ID = 1) is shown in Figure 4.
Figure 4. State estimation error for the Mars approach phase (Halo-Halo-VP-VP constellation).
The obtained RMS position error for the Mars approach phase is 937·1 m and the obtained RMS velocity error is 21·5 mm/s. The probability of the state estimation error falling inside the 3σ line is 100% for every component and due to the same reason as before, the x-axis state estimation error is also smaller than the other two directions. To compare the navigation performance of different constellation configurations and measurement types, we also perform N = 1000 identical MC simulations for every candidate constellation and the final results are summarised in Table 8.
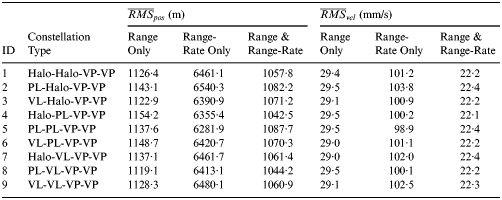
Table 8. Navigation results for the Mars approach phase (N = 1000 MC runs).
From the table, it can be seen that the Mars final approach navigation results are close for different constellation configurations. The best navigation accuracy is always achieved by combined range and range-rage measurements, with the average RMS position error about 1060 m and the average RMS velocity error about 22 mm/s. When only range or range-rate measurements are used for Mars approach navigation, the resulting state estimation error is apparently larger. Therefore, the combined range and range-rate tracking data are the preferred measurements for Mars approach navigation.
5.4. Mars Orbit Navigation Performance
The last mission phase is the Mars orbit phase. After the MOI manoeuvre, the spacecraft is inserted into the target Mars orbit and the visibility of the four libration point navigation satellites during the Mars orbit phase is shown in Figure 5.
Figure 5. Timeline of visible libration point satellites during the Mars orbit phase. Only the first 12 hour interval is shown in the figure. For longer periods, the results are similar.
From the figure, it can be seen that, due to the obscuration of Mars, there are 50 minute invisible periods and 60 minute visible periods which appear alternately during the Mars orbit phase. Therefore range and range-rate tracking data can only be obtained as the spacecraft passes in front of Mars. During the visible period, observations are taken at 10-minute intervals. After generating the tracking data, a Mars orbit navigation simulation is conducted for the candidate Earth-Moon L 1,2,4,5 four-satellite constellations.
Figure 6 shows the navigation results of the Halo-Halo-VP-VP constellation (ID = 1). To illustrate the filter performance more clearly, only the first 12 hour results are shown in the figure. The RMS position error for the Mars orbit phase is 42·1 m and the RMS velocity error is 39·6 mm/s. The probability of the position estimation error falling inside the 3σ line is 99·49%, 99·77% and 99·77%, respectively for the x, y and z components, while the probability of the velocity estimation error falling inside the 3σ line is 99·77%, 99·84% and 99·77%, respectively for the vx, vy and vz components. Based on the same parameters, navigation performance of different constellation types is evaluated by MC simulations and the final results are summarised in Table 9.
Figure 6. State estimation error for the Mars orbit phase (Halo-Halo-VP-VP constellation).
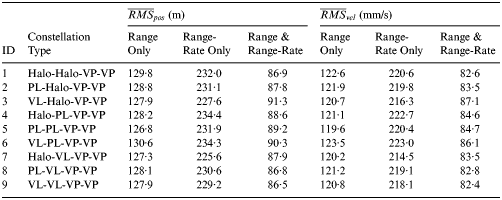
Table 9. Navigation results for the Mars orbit phase (N = 1000 MC runs).
From the results, it can be seen that the combined range and range-rate measurements also present a superior performance compared with the single measurements, with the average RMS position error about 88 m and the average RMS velocity error about 84 mm/s. Also, the Mars orbit navigation performance is also similar for different constellation configurations. Consequently, we can come to the conclusion that, with the use of appropriate tracking data, the candidate Earth-Moon L 1,2,4,5 four-satellite constellations are available for Mars navigation.
6. CONCLUSIONS
This paper presents a feasibility study of using the libration point satellite navigation system for Mars exploration navigation. Based on the reference Mars mission scenario, navigation performance of the candidate Earth-Moon L 1,2,4,5 four-satellite constellations is evaluated by MC simulations. The final results demonstrate the availability and superiority of the libration point satellite navigation system:
(1) It enables autonomous on board navigation without relying on Earth-based tracking data, which can substantially lower the operation cost for deep-space missions;
(2) By using the combined range and range-rate tracking data, the libration point satellite navigation system can provide a high-performance navigation support for future Mars exploration.
Due to the independent and extended navigation capability, the libration point satellite navigation system may have a great potential in the future.
The current work is mainly based on the circular restricted three-body problem. In this model, the periodic motions around the libration points are conditionally stable. However, considering the perturbations due to other celestial bodies and solar radiation pressure, libration point satellites may gradually drift away from their nominal orbits. Therefore, orbital correction manoeuvres are indispensable and station-keeping strategies for the libration point navigation satellites will be considered in the succeeding work.
ACKNOWLEDGMENTS
This work was carried out with financial support from the National Basic Research Program 973 of China (2013CB834103).
